Physics VELOCITY-TIME, POSITION TIME AND ACCELERATION-TIME GRAPHS

Position-Time Graph (x-t graph)

Slope of tangent drawn at any point on the curve of the x-t graph gives instantaneous velocity and magnitude
of slope gives instantaneous speed.

`text(Description of motion using)` x-t `text(graph :)`

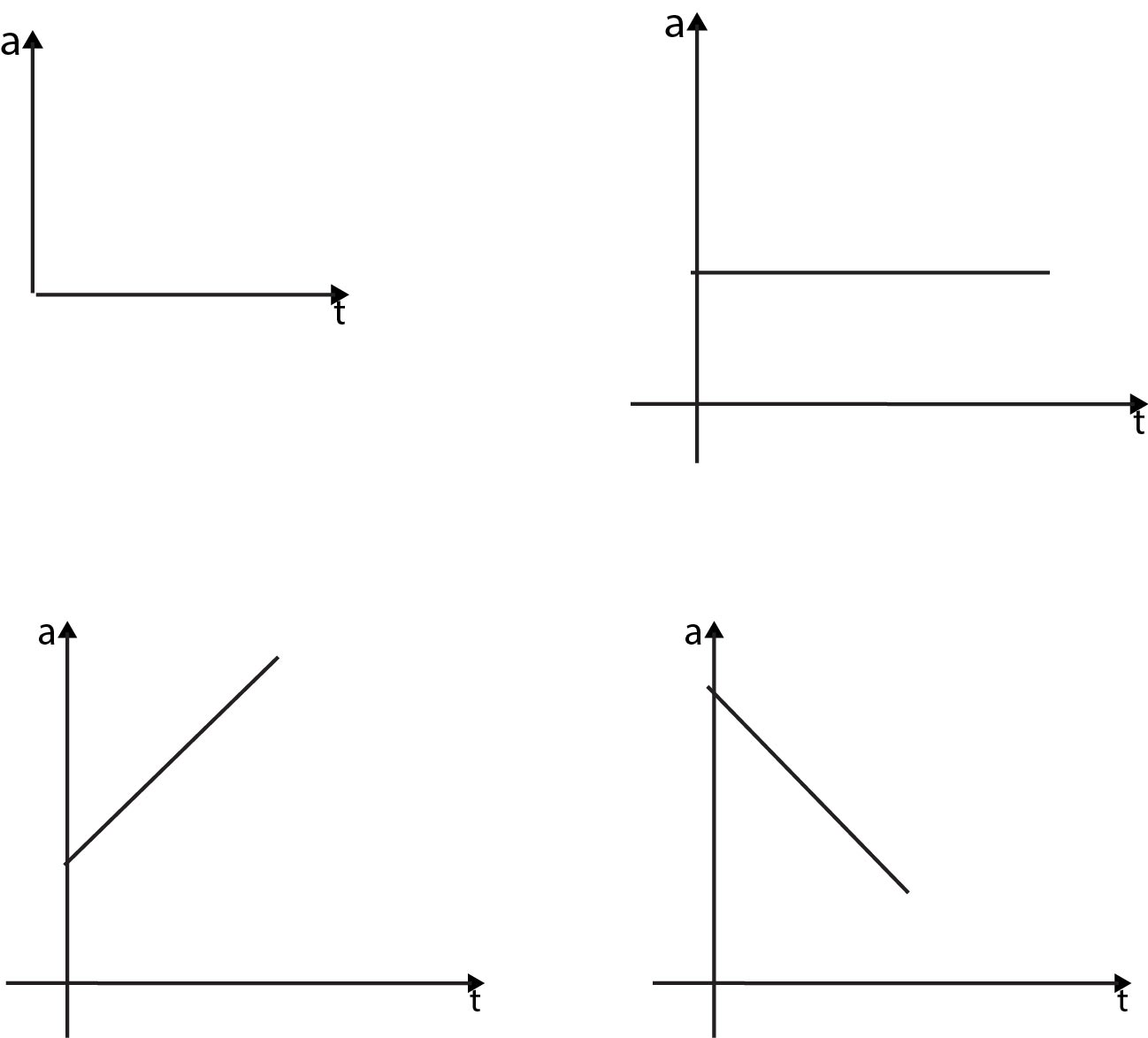
`text((A))` Particle at rest.

`(dx)/(dt) =0`, particle at rest

`text((B))` Particle moving with uniform velocity in the positive direction.

`(dx)/(dt) =` position constant

`text((C))` Particle moving with uniform velocity in negative direction.

`text((D))` Particle moving with uniform acceleration.
Slope at B is greater than slope at A, implying acceleration.

`text((E))` Particle moving with uniform retardation.

Slope at B is less than slope at A, implying retardation.

`text((F))` Particle moving with uniform acceleration in negative direction.

Magnitude of slope at B is greater than that at A, but motion is in negative direction.

`text((G))` Particle moving with uniform retardation in negative direction.
Slope at B is less than that of A. Motion is in the negative direction.

`text((H))` These x-t graphs are not possible.
Slope is infinite, implying infinite velocity, which is not possible.
Particle is at two positions `x_1`, and `x_2` , at a given time instant `t_1`, which is not possible.

Velocity-Time Graph (v-t graph)

`(dv)/(dt) = v,` Slope of `v - t` graph gives instantaneous acceleration

`(ds)/(dt) =v` `int ds= int vdt` `intvdt =s`

Area under `v -t` graph gives displacement.

Thus `v - t` graph gives us instantaneous velocity, instantaneous acceleration as well as displacement covered. Hence `v - t` graphs can be effectively utilized in solving problems.

`text(Description of motion with v - t graph :)`

`text((A))` Particle at rest.

`text((B))` Particle moving with uniform velocity.

`(dv)/(dt) =0`, acceleration is zero.

`text((C))` Particle moving with uniform acceleration.
Slope of above graph is constant and positive, implying uniform acceleration.

`text((D))` Particle moving with uniform retardation.
Slope of above graph is constant and negative, implying uniform retardation.

`text((E))` Particle moving with increasing acceleration.
Slope at A is less, slope at B is more, implying increasing acceleration.

`text((F))` Particle moving with decreasing acceleration.
Slope at B is less than that at A implying decreasing acceleration.

Acceleration-Time Graph (a-t graph)

`text((A))` Particle with zero acceleration. (rest or uniform velocity)

`text((B))` Particle moving with uniform acceleration.

`text((C))` Particle moving with increasing acceleration.

`text((D))` Particle moving with decreasing acceleration.

Area Under Various Graphs

`(dv)/(dt) =a =>int_u^v dv = int_0^t adt=>v-u= int a dt`

Area under `a - t` graph gives change in velocity.

`a= v ((dv)/(ds))=>int a ds = int_u^v vdv`

`int a ds = (v^2-u^2)/2`

Area under `a - s` graph `= (v^2-u^2)/2`
Where, `v` is instantaneous velocity and `u` is initial velocity.

`(ds)/(dt) =v`

`int ds = int v dt=>s= int v dt`

Area under `v - t` graph gives displacement.