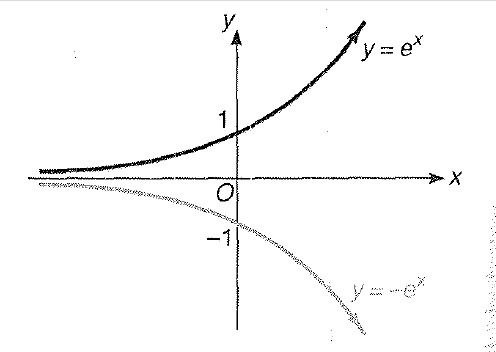
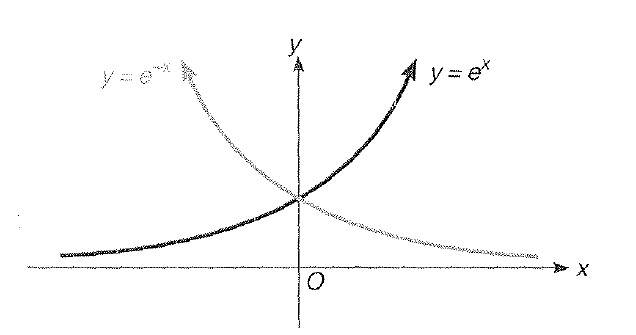
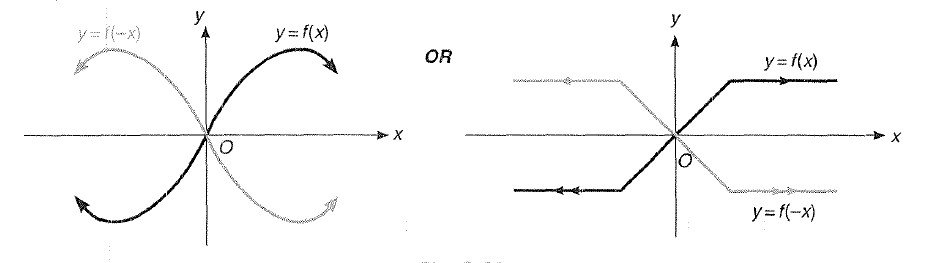
Modulus Functions
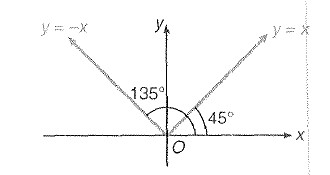
Absolute value function (or modulus function)
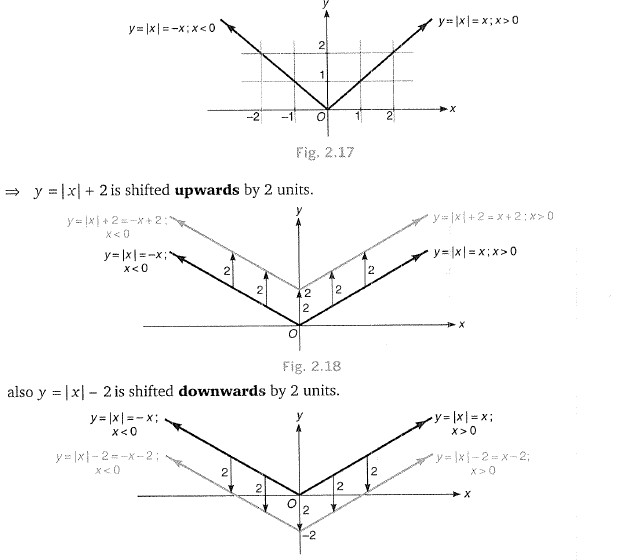
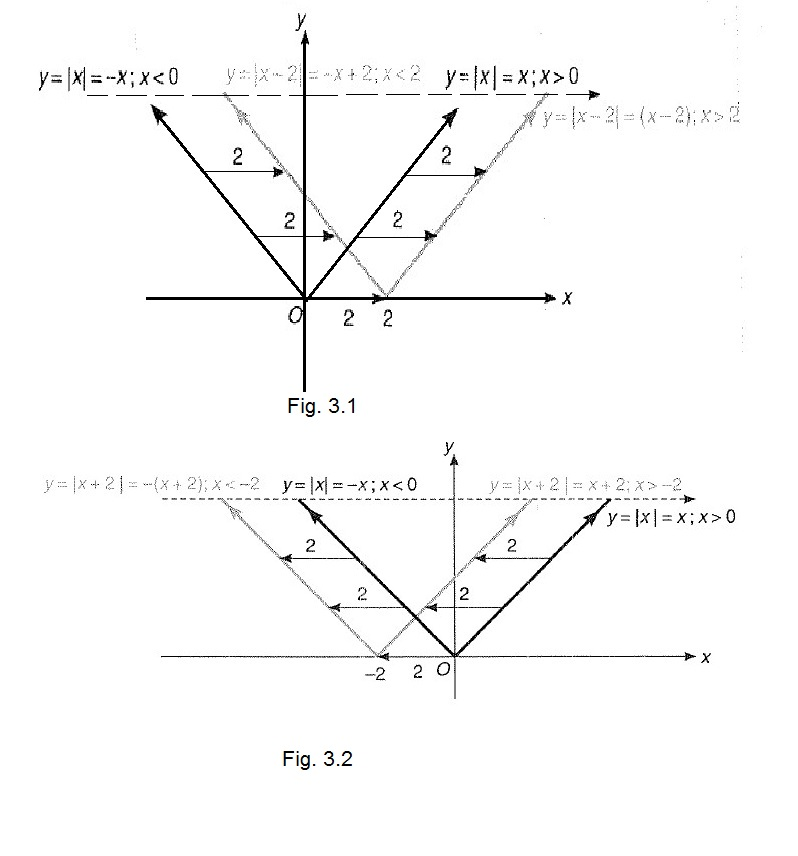
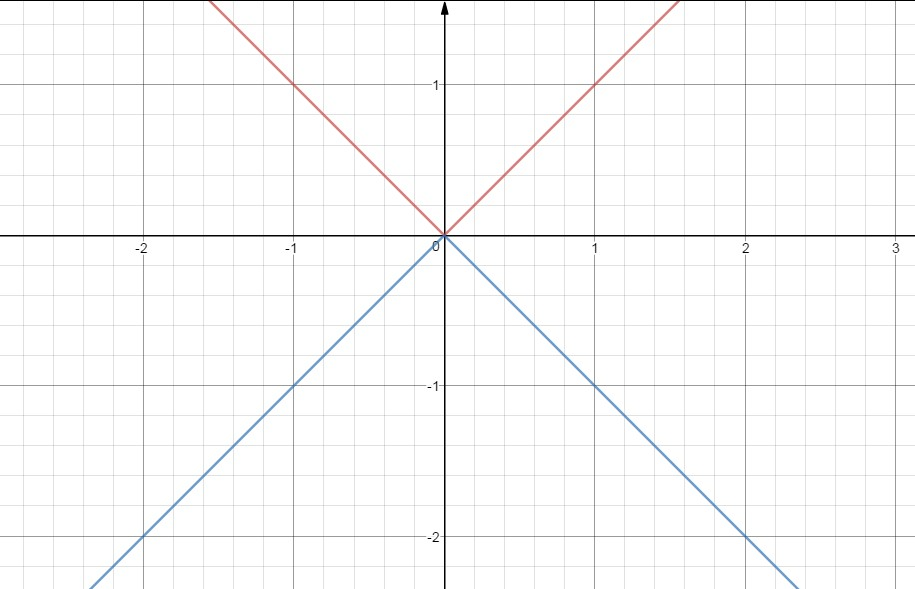
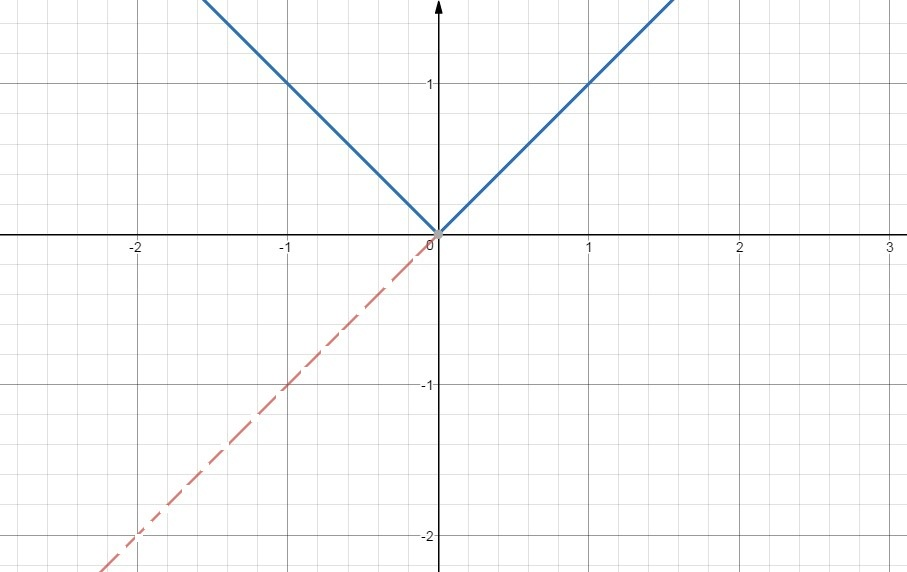
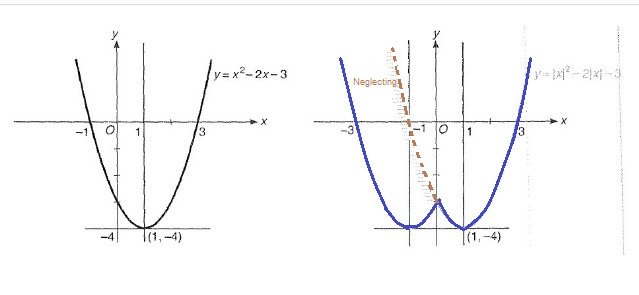
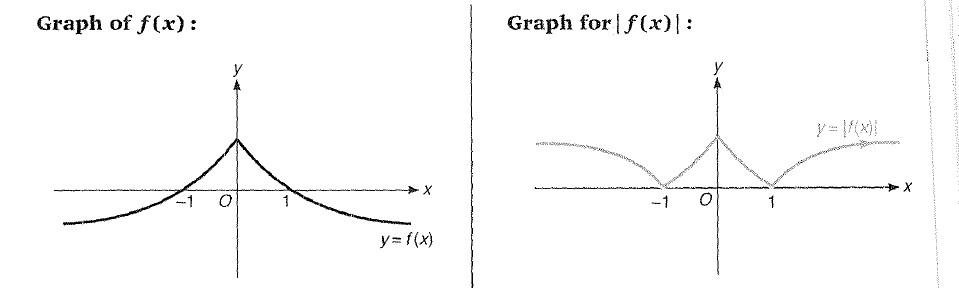
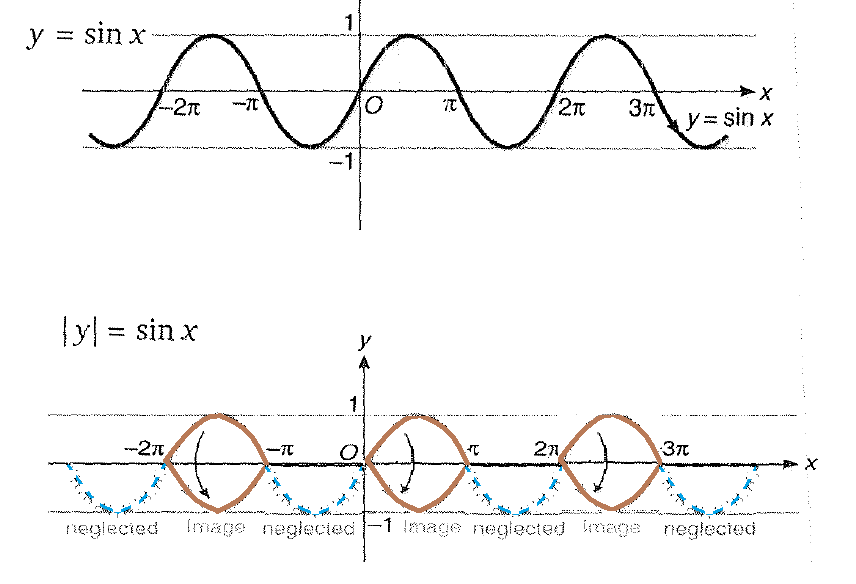
`y= |x| = { tt((x, x ge 0),(-x, x <0))`
It is the numerical value of `x`
It is symmetric about `y`-axis"
Its domain is in `R` and range `[0, oo)`.
Properties of modulus functions
(i) `| x| le a => -a le x le a ; (a ge 0)`
(ii) `|x| ge a => x le -a` or `x ge a ; (a ge 0)`
(iii) `|| x| - | y|| le |x ± y | le | x | + | y |`
`y= |x| = { tt((x, x ge 0),(-x, x <0))`
It is the numerical value of `x`
It is symmetric about `y`-axis"
Its domain is in `R` and range `[0, oo)`.
Properties of modulus functions
(i) `| x| le a => -a le x le a ; (a ge 0)`
(ii) `|x| ge a => x le -a` or `x ge a ; (a ge 0)`
(iii) `|| x| - | y|| le |x ± y | le | x | + | y |`