Complex Number and Its Representation
A number in the form of `z = x + iy,` where `x, y in R, i = sqrt(-1)` is called complex number. The real numbers `x` and `y` are respectively called real and imaginary parts of complex number `z.`
i.e `x =Re(z)` and `y = Im(z)`
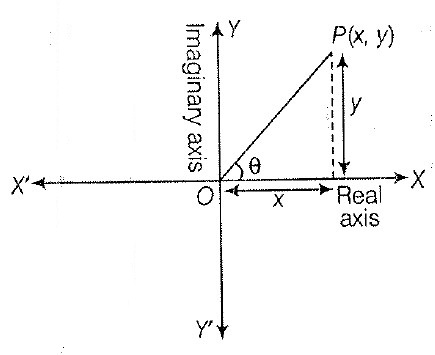
The complex number `z = x + iy` is represented by a point `P, `whose coordinates are referred to rectangular axes `XOX'` and `YOY'` which are called real and imaginary axes, respectively.
This plane is called argand plane or Gaussian plane. The magnitude of the complex number `z` is `|z| = sqrt(x^2 + y^2)` and `theta = tan^(-1)( y/x)`
A complex number `z` is said to be purely real or imaginary, if `y = 0` or `x = 0`, respectively.
`text(Integral Powers of i)` We know that, `i = sqrt(-1) , i^2 = -1, i^3 = -i, i^4 = 1` etc
In general `i^(4n) = 1, i^(4n +1) =i , i^(4n +2) = -1, i^(4n +3) = - i , AA` any integer n
The sum of four consecutive powers of `i` is zero. i.e `i^n + i^(n +1) + i^(n +2) + i^(n +3) = 0, n in I`
i.e `x =Re(z)` and `y = Im(z)`
The complex number `z = x + iy` is represented by a point `P, `whose coordinates are referred to rectangular axes `XOX'` and `YOY'` which are called real and imaginary axes, respectively.
This plane is called argand plane or Gaussian plane. The magnitude of the complex number `z` is `|z| = sqrt(x^2 + y^2)` and `theta = tan^(-1)( y/x)`
A complex number `z` is said to be purely real or imaginary, if `y = 0` or `x = 0`, respectively.
`text(Integral Powers of i)` We know that, `i = sqrt(-1) , i^2 = -1, i^3 = -i, i^4 = 1` etc
In general `i^(4n) = 1, i^(4n +1) =i , i^(4n +2) = -1, i^(4n +3) = - i , AA` any integer n
The sum of four consecutive powers of `i` is zero. i.e `i^n + i^(n +1) + i^(n +2) + i^(n +3) = 0, n in I`