`z^n-1=0 =>\ \ \ \ \ \ z=(1)^(1/n)=(cos0+isin0)^(1/n)=(cos2mpi+i sin 2mpi)^(1/n)`
`=>cos((2mpi)/n)+i sin ((2mpi)/n) ,\ \ \ \ m=0, 1, 2 , 3 ,............,(n-1)`
`m = 0, z_1 = 1`
`m=1 , z_2= cos((2pi)/n)+i sin ((2pi)/n)= e^(i(2pi)/n)=alpha(Let)`
`m=2 , z_3= cos((4pi)/n)+i sin ((4pi)/n)= e^(i(4pi)/n)=alpha^2(Let)`
` .`
` .`
`. `
` .`
` .`
` .`
`. `
` .`
`m= (n - 1), z_n = cos((2(n-1)pi)/n)+i sin ((2(n-1)pi)/n)= e^(i((2(n-1)pi)/n))=alpha^(n-1)(Let)`
`text(Important Results : )`
`1.` If `1, alpha_1, alpha_2,alpha_3,..........,alpha_(n-1)` nth roots of unity, then
`(1)^p + (alpha_1)^p + (alpha_2)^p + ......+ (alpha_(n-1))^p = { tt[(0, text{if pis not an integral multiple of n}),(n,text{1f p is an mtegral multiple of n})]`
`2. (1 + alpha_1)(1-alpha_2).............(1- alpha_(n-1)) = { tt[(0, text{if n is even}),(1,text{if n is odd})]`
`3.(1-alpha_1)(1-alpha_2)..........(1-alpha_(n-1)) = n`
`4. z^n -1 = (z-1)(z+1) Pi_(r=1)^(n-2)//2(z^2 - 2z cos (2rpi)/n + 1)` if 'n' is even
`5.z^n +1 = Pi_(r=1)^((n-2)//2)(z^2-2z cos(((2r+1)pi)/pi)+1),` if n even
`6.z^n +1 = Pi_(r=0)^((n-3)//2)(z^2-2z cos(((2r+1)pi)/pi)+1),` if 'n' odd
`text(The Sum of the Following Series Should be Remembered : )`
`(i) cos theta + cos 2 theta + cos 3 theta + .........+ cos n theta = (sin((n theta)/2))/(sin(( theta)/2)) . cos[((n+1)/2)theta]`
`(ii) sin theta + sin 2 theta + sin 3 theta + .........+ cos n theta = (sin((n theta)/2))/(sin(( theta)/2)) . sin[((n+1)/2)theta]`
`z^n-1=0 =>\ \ \ \ \ \ z=(1)^(1/n)=(cos0+isin0)^(1/n)=(cos2mpi+i sin 2mpi)^(1/n)`
`=>cos((2mpi)/n)+i sin ((2mpi)/n) ,\ \ \ \ m=0, 1, 2 , 3 ,............,(n-1)`
`m = 0, z_1 = 1`
`m=1 , z_2= cos((2pi)/n)+i sin ((2pi)/n)= e^(i(2pi)/n)=alpha(Let)`
`m=2 , z_3= cos((4pi)/n)+i sin ((4pi)/n)= e^(i(4pi)/n)=alpha^2(Let)`
` .`
` .`
`. `
` .`
` .`
` .`
`. `
` .`
`m= (n - 1), z_n = cos((2(n-1)pi)/n)+i sin ((2(n-1)pi)/n)= e^(i((2(n-1)pi)/n))=alpha^(n-1)(Let)`
`text(Important Results : )`
`1.` If `1, alpha_1, alpha_2,alpha_3,..........,alpha_(n-1)` nth roots of unity, then
`(1)^p + (alpha_1)^p + (alpha_2)^p + ......+ (alpha_(n-1))^p = { tt[(0, text{if pis not an integral multiple of n}),(n,text{1f p is an mtegral multiple of n})]`
`2. (1 + alpha_1)(1-alpha_2).............(1- alpha_(n-1)) = { tt[(0, text{if n is even}),(1,text{if n is odd})]`
`3.(1-alpha_1)(1-alpha_2)..........(1-alpha_(n-1)) = n`
`4. z^n -1 = (z-1)(z+1) Pi_(r=1)^(n-2)//2(z^2 - 2z cos (2rpi)/n + 1)` if 'n' is even
`5.z^n +1 = Pi_(r=1)^((n-2)//2)(z^2-2z cos(((2r+1)pi)/pi)+1),` if n even
`6.z^n +1 = Pi_(r=0)^((n-3)//2)(z^2-2z cos(((2r+1)pi)/pi)+1),` if 'n' odd
`text(The Sum of the Following Series Should be Remembered : )`
`(i) cos theta + cos 2 theta + cos 3 theta + .........+ cos n theta = (sin((n theta)/2))/(sin(( theta)/2)) . cos[((n+1)/2)theta]`
`(ii) sin theta + sin 2 theta + sin 3 theta + .........+ cos n theta = (sin((n theta)/2))/(sin(( theta)/2)) . sin[((n+1)/2)theta]`











 True
True False
False

 True
True False
False

 True
True False
False


















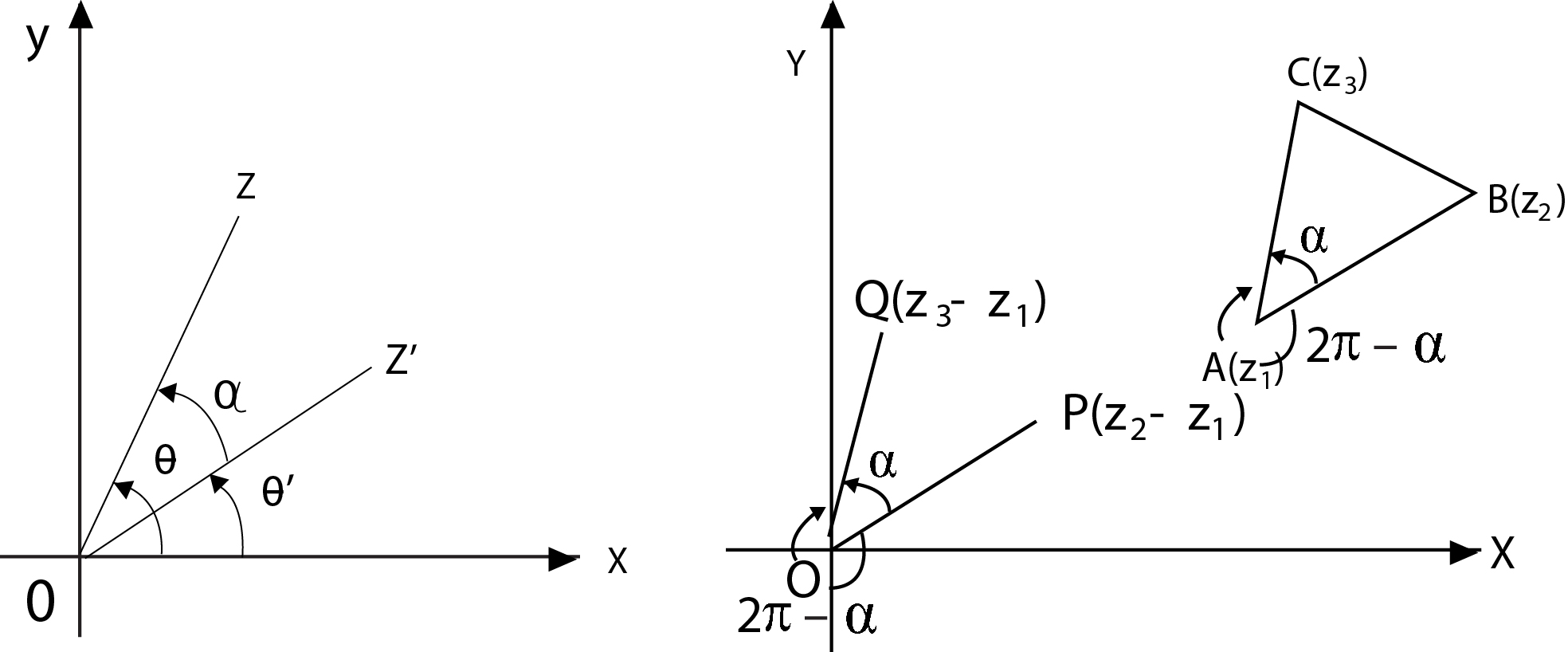














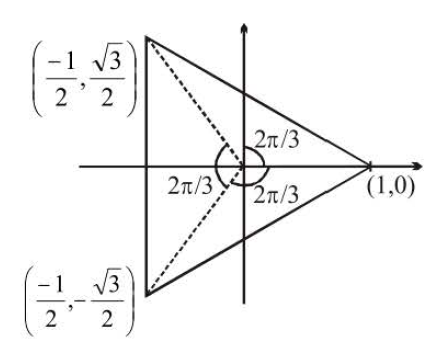

 True
True False
False













 Both A and R individually true and R is the correct explanation of A
Both A and R individually true and R is the correct explanation of A Both A and R are individually true but R is not the correct explanation of A
Both A and R are individually true but R is not the correct explanation of A A is true but R is false
A is true but R is false A is false but R is true
A is false but R is true







 True
True False
False





































































































































