Mathematics Advanced Discussion for IIT JEE Part II :
Please Wait... While Loading Full Video

Advanced Discussion for IIT JEE Part II :

Vectorial Representation of a Complex Number :

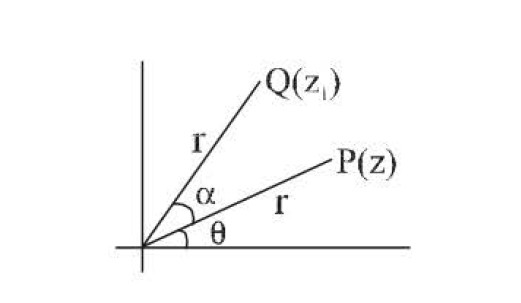
Every complex number can be considered as if it is the position vector of that point. If the point `P` represents the complex number `z` then,

`vec(OP)=z` & `| vec (OP)| = |z|`
Q 2610191910

If `(z_1,z_2)` and `(z_3 ,z_4)` are two pairs of non zero conjugate complex number's then `arg (z_1/z_3)+ arg (z_2/z_4)= pi//2`

(A) True
(B) False
Solution:

`bar z_1 =z_2 , bar z_3 =z_4`

`arg (z_1/z_3) + arg (z_2/z_4)=arg ((z_1z_2)/(z_3z_4))=arg ((z_1bar z_1)/(z_3 bar z_3))=0`
Correct Answer is `=>` (B)

Geometry of Complex Number :

`OP=| z_1+ z|`

`OP=P_2P_1 =| z_1-z_2|`

`|OP_1 -OP_2| le OP or P_1P_2 le OP_1 + OP_2`

`| |z_1| -|z_2| | le |z_1 pm z_2| le |z_1 | + | z_2| `

Centroid, Incentre, Orthocentre & Circumcentre of a triangle on a complex plane :

(i) Centriod `'G' =(z_1+z_2+z_3)/3`


(ii) Incentre `'I' = (az_1+bz_2+cz_3)/(a+b+c)`














(iv) Circumcentre : `|z_1-z_0| =|z_2-z_0| =|z_3-z_0|`

Q 1147012883

If the complex numbers `z_1, z_2, z_3` represent the vertices of an equilateral triangle such that ` | z_1 | = | z_2 | = | z_3 | ` then `z_1 + z_2 + z_3 = ` ` (Given, ω is non - real cube root of unity)

(A)

`1`

(B)

`ω`

(C)

`ω^2`

(D)

`0`

Solution:

`| z_1 | = | z_2 | = | z_3 | `

⇒ origin O is the circumcentre.

Thus centroid will be at origin

`(z_1+z_2+z_3)/3=0`

`⇒ z_1 + z_2 + z_3 = 0`
Correct Answer is `=>` (D) `0`
Q 1107812788

If `z_1, z_2` and `z_3` are the vertices of a triangle ABC such that `| z_1 | = | z_2 | = | z_3 |` And AB = AC, then

(This question may have multiple correct answers)

(A) `(z_2z_3)/z_1^2` is purely imaginary
(B) Orthocentre of ∆ABC is a `z_1 + z_2 + z_3`
(C) `((z_1+z_3)(z_1+z_2))/(z_2+z_3)^2` is purely real
(D) None of these
Solution:

`| z_1 | = | z_2 | = | z_3 |` ⇒ origin is the circumcentre of ∆ABC

⇒ orthocentre H of ∆ ABC is `z_1 + z_2 + z_3` ( as distance between orthocentre and centroid is twice that of distance between centroid and circumcentre )

Now `∠AHB = ∠CHA`

`⇒arg((z_1+z_2+z_3−z_2)/(z_1+z_2+z_3−z_1))=arg((z_1+z_2+z_3−z_1)/(z_1+z_2+z_3−z_3))`

`⇒arg(((z_1+z_3)(z_1+z_2))/((z_2+z_3)^2))=0`

Similarly `∠AOB = ∠COA⇒(z_2z_3)/z_1^2` is purely real.

Orthocentre of ∆ABC is a `z_1 + z_2 + z_3, ((z_1+z_3)(z_1+z_2))/((z_2+z_3)^2)` is purely real
Correct Answer is `=>` (B)

Equation of a straight line with the help of rotation formula :

`arg ((z-z_1)/(z_2-z_1))= 0` or `pi`

`=> (z-z_1)/(z_2-z_1)` is purely real .

`=> (z-z_1)/(z_2-z_1) =(bar z -bar z_1)/(bar z_2 - bar z_1)`

Condition for which two lines which are parallel :

Since `AB` and `CD` lines are parallel

`:. arg ((z_1-z_2)/(z_3-z_4))=0` or `pi => (z_1-z_2)/(z_3-z_4)` is purely real `=> (z_1-z_2)/(z_3-z_4) = ((bar z_1 - bar z_2)/(bar z_3- bar z_4))`

Condition for which two lines which are perpendicular :

Since lines `AB` and `CD` are perpendicular

`arg ((z_1-z_2)/(z_3-z_4))= pm pi/2`

`=> (z_1 -z_2)/(z_3-z_4)` is purely imaginary.

`=> (z_1-z_2)/(z_3-z_4) = - ((bar z_1 - bar z_2)/(bar z_3 - bar z_4))`

General equation of the line :

`bar a z + a bar z + b=0 , b in R and a in C`

`ax+by+c=0`

`a-> bar a, b-> bar b , c-> bar c`

`x-> z , y-> bar z`

Complex slope of a line `= -a/(bar a)`

Complex slope of a line passing through `A(z_1) ` & `B(z_2)` is given by

`omega=(z_1-z_2)/(bar z_1 - bar z_2)`

Complex slope of a line making an angle `theta` from positive real axis is

`omega= e^(i 2 theta)`

Let `omega_1` and `omega_2` be the complex slopes of two lines then

(i) If `omega_1 = omega_2` then lines are parallel

(ii) If `omega_1 + omega_2 = 0` then lines are perpendicular
Q 1167323285

If the lines `abarz+baraz+b=0` and `cbarz+barcz+d=0` are mutually perpendicular, Where a and c are non - zero complex numbers and b and d are real numbers, Then

(This question may have multiple correct answers)

(A) `abarc` is purely imaginary
(B) `abara+cbarc=0`
(C) `abara=cbarc`
(D) `arg(a/c)=±π/2`
Solution:

Let `a = a_1 + ia_2` and `c = c_1 + ic_2`

then slope of the line `abarz+baraz+b=0` is `−a_1/a_2`

and slope of the line `cbarz+barcz+d=0` is `−c_1/c_2`

So `−a_1/a_2×−c_1/c_2=−1 `

`⇒a_1c_1+a_2c_2=0`

`⇒((a+bara)/2)((c+barc)/2)+((a−bara)/(2i))((c−barc)/(2i))=0`

`⇒abarc+barac=0`

`abarc` is purely imaginary.

Also

`a/c=−bar((a/c))⇒a/c` is also purely imaginary

`⇒arg(a/c)=±π/2`
Correct Answer is `=>` (A)
Q 2680167017

If z is a complex number satisfying `|z- i Re (z) | = |z- lm (z)|` then z lies on

(A)

y = x

(B)

y = - x

(C)

y = x + 1

(D)

y = - x + 1

Solution:

`| z - iRe (z) | = | z- lm (z) |`

Let `z = x + iy`, then

`|x + iy - ix| = | x + iy - y|`

i.e. `x^2 + (y- x^2) = (x- y)^2 + y^2`

i.e. `x^2 = y^2` i.e. `y = ± x`
Correct Answer is `=>` (A)
Q 1107012888

If `| z^2 - 1 | = | z |^2 + 1`, then locus of `z` is

(A)

Circle

(B)

Imaginary axis

(C)

Real axis

(D)

None of these

Solution:

`| z^2 - 1 | = | z^2 | + 1`

Distance between` P ( z^2 )` and `Q (i)` is equal to sum of distance of `P` and `Q` from origin. Thus P `( z^2 )` lies on the negative real axis so

`Im ( z^2 ) = 0` and `Re ( z^2 ) ≤ 0`

`xy = 0` and `x^2 - y^2 ≤ 0 ⇒ x = 0`

`z` would lie on imaginary axis.
Correct Answer is `=>` (B) Imaginary axis

Parametric Form of Straight line :

If `z` divides `z_1` and `z_2` in the ratio `t : 1-t ; (0 < t < 1)`

then `z= (1-t)z_1 + t z_2`

Reflection Points For a Line (Image of a point in a line) :

Two given points `P` & `Q` denoted by complex numbers `z_1` and `z_2` respectively are the reflection points in a given straight ` bar alpha z +alpha bar z + r =0` if the given line is the right bisector of the line segment `PQ`. Two points `P(z_1)` & `Q (z_2)` will be the reflection points of each other in the given straight line,

if `bar alpha z_1 + alpha bar z_2 + r = 0` where `'r'` is real and a is non zero complex constant.








Proof : `M` is the mid point of `PQ` which lies on the line mirror

`:, bar alpha ((z_1+z_2)/2)+ alpha ((bar z_1 + bar z_2)/2)+ r=0`

`bar alpha z_1 + bar alpha z_2 + alpha bar z_1 + alpha bar z_2 + 2r=0`..................(i)

`:. (z_1-z_2)/(bar z_1- bar z_2) + (- alpha/(bar alpha))=0`

`z_1 bar alpha -z_2 bar alpha = alpha bar z_1 - alpha bar z_2`

`alpha bar z_1 + bar alpha z_2 = alpha bar z_2 + bar alpha z_1`...........................(ii)

From (i) & (ii)

`1 ( bar alpha z_2 + alpha bar z_1)+ 2r=0`

`=> alpha bar z_1 + bar alpha z_2+ r=0`
Q 2630856712

Image of the point, whose affix is ` (2 - i)/(3 + i)` , in the line `(1 + i) z + (1 - i) barz = 0` is the point whose affix is

(A)

` (1 + i)/2`

(B)

` (1 - i)/2`

(C)

` (-1 + i)/2`

(D)

` -(1 + i)/2`

Solution:

Equation of the line is `2x- 2y = 0` i.e ` y = x`

Now ` (2- i)/(3 + i) =( (2- i)(3- i))/(10) = (1 - i)/2`

`:.` image is the point whose affix is `(-1 + i)/2`
Correct Answer is `=>` (C) ` (-1 + i)/2`
Q 1147812783

The reflection of the complex number `(4+3i)/(1+2i)` in the straight line `iz=barz` ,is

(A)

`2 + i`

(B)

`4 - 2i`

(C)

`3 - 4i`

(D)

`1 - 2i``

Solution:

`((4+3i)(1−2i))/((1+2i)(1−2i))=(4+3i−8i+6)/(1+4)=2−i`

`iz=barz`

`I ( x + iy ) = x - iy`

`ix - y = x - iy`

`x = y - i ( x + y) = 0`

`x + y = 0`

Reflection is `( 1 - 2i )`
Correct Answer is `=>` (D) `1 - 2i``

Distance of a given point from a given line :

Let the given line be `z bar a + bar za + b = 0`, and the given point be `z_c`

Say `z_c = x_c+iy_c`.

Replacing `z` by `x + iy`, in the given equation,

we get, `x(a + a) + iy(bar a - a) + b= 0`

Distance of `(x_c, y_c) ` from this line is,

`(|x_c (a+ bar a) + iy_c ( bar a -a)+ b|)/(sqrt (a+ bar a)^2 -(a- bar a)^2)`

`= (|z_c bar a+ bar z_c a+ b|)/( sqrt ( 4(Re(a))^2+ 4 (im (a))^2))`

`= (|z_c bar a + bar z_c a + b|)/(2 |a|)`
Q 2650278114

Consider a line `(1 + i)z - (1 - i) bar z + 2i = 0`. Find the distance of a point `2i` from the above line

Solution:

The given line can be written as `(1-i) z+ (1+i) bar z +2=0`

Applying distance formula

`d= (|z_c bar alpha + z_c alpha + b|)/(2 | alpha|)`

`= |((1-i)2i +(1+i)(-2i)+2)/(2 sqrt 2)| =|(2i +2 -2i+2+2)/(2 sqrt 2)| = 3/ sqrt 2`

Different forms of equation of a circle :

(i) `|z| = r, r in R^+` then locus of `z` represent a circle whose centre is the origin and radius is equal to `r`.



(ii) `| z- z_0| = r, r in R^+` then locus of `z` represents a circle whose centre is `z_0` and radius is equal to `r`.


(iii) Equation `z bar z +a bar z + bar a z + b = 0` represent a circle whose centre is `- a` and radius is equal `sqrt(|a|^2-a)`

Equation of the circle with centre `z_0` and radius `'r'`.

`|z-z_0|=r => |z-z_0|^2 =r^2=> (z-z_0)(bar z - bar z_0)=r^2=> z bar z - z bar z_0 - bar z z_0 + |z_0|^2 -r^2=0`

Putting `- z_0 = a` and `|z_0|^2 - r^2 = b` equation becomes `z bar z + bar a z + a bar z + b = 0`

`:.` Centre `z_0 =-a` and radius `r= sqrt(|z_0|^2 -b) = sqrt(|a|^2-b)`
Q 2650456314

If 'z' is complex number then then locus of 'z' satisfying the condition `|2z- 1| = | z - 1 |` is

(A)

perpendicular bisector of line segment joining `1/2` and `1`

(B)

circle

(C)

parabola

(D)

none of the above curves

Solution:

` 2| z - 1/2 | = | z - 1| :. ( |z-1|)/(|z - 1/2|) = 2 `

So Locus of z is a circle.
Correct Answer is `=>` (B) circle
Q 2680756617

If ` ( z - (1 + i))/(z + (1 - i))` is pure imaginary, then z lies on

(A)

a straight line

(B)

a cricle

(C)

a line segment

(D)

None of these

Solution:

If ` ( z - (1 + i))/(z + (1 - i))` is pure imaginary` => ( z - (1 + i))/(z + (1 - i)) + (bar z - (1 - i))/(bar z + (1 - i)) = 0`

`=> z bar z + z(1- i) - bar z(1 + i)- 2 + z bar z (1 - i) bar z + (1 + i) bar z- 2 = 0`

`=> z bar z = 2`

`:. z` lies on a circle
Correct Answer is `=>` (B) a cricle
Q 2650156914

If `t` and `c` are two complex numbers such that `| t | != |c| , | t | = 1` and `z = (at + b) /(t -c) , z = x + iy`. Locus of `z` is
(where a, b are complex numbers)

(A)

line segment

(B)

straight line

(C)

circle

(D)

none

Solution:

`z = (at + b)/(t -c) => t = ( b + cz)/(z -a)`

` | t | = 1 => t t = 1 => ((b + cz)(bar b + bar c bar z))/( (bar z- bar a)(z - a)) =1`

`=> z bar z (c bar c - 1) + (c bar b +bar a)z + (barc b + a) barz+b bar b - a bar a = 0`
Correct Answer is `=>` (C) circle
Q 2650456314

If 'z' is complex number then then locus of 'z' satisfying the condition `|2z- 1| = | z - 1 |` is

(A)

perpendicular bisector of line segment joining `1/2` and `1`

(B)

circle

(C)

parabola

(D)

none of the above curves

Solution:

` 2| z - 1/2 | = | z - 1| :. ( |z-1|)/(|z - 1/2|) = 2 `

So Locus of z is a circle.
Correct Answer is `=>` (B) circle

Diametric form of equation of circle :

Let `A(z_1)` and `B(z_2)` are the extremities of diameter of a circle and `P(z)` be a variable point then

(a) `CP = r` (`r=` radius of the circle)

`| z - (z_1+z_2)/2| =|(z_1-z_2)/2|`

(b) `AP` & `BP` are Perpendicular

`:. omega_1 + omega_2 =0 => (z-z_1)/(bar z- bar z_1) + (z-z_2)/( bar z- bar z_2)=0`

(c) `AP^2 + BP^2=AB^2`

`| z-z_1|^2 +|z-z_2|^2 =|z_1-z_2|^2`
Q 1406223178

Let `z_1 = 6 + i` and `z_2 = 4- 3i` . Let `z` be a complex number such that `arg ((z-z_1) /(z_2-z)) = pi/2` , then `z` sati.sfies

(A)

`|z-(5-i)|=5`

(B)

`|z-(5-i)|=sqrt5`

(C)

`|z-(5+i)|=5`

(D)

`|z-(5+i)|=sqrt 5`

Solution:

`arg ((z-z_1)/(z_2-z))=pi/2`

`:. z_1, z_2, z_3` lie on a circle.

`=> z_1` and `z_2` are the end points of diameter

`:.` centre `(z_0)=(z_1+z_2)/2`

`:. z_0=5-i`

and radius `=| z_1 - z_0 |`

`=|1 + 2i|`

`r=sqrt 5`

`:.` Equation circle is `| z - z_0 | = r`

or ` |z-(5-i)|=sqrt5`
Correct Answer is `=>` (B) `|z-(5-i)|=sqrt5`

Equation of circle passing through three non-collinear points :

Let `A(z_1), B(z_2)` and `C(z_3)` be three given non-collinear points and `P(z)` be a variable point. Angle subs tended by the are `AP` at `B` and `C` are equal (say `'alpha '`)

Using rotation theorem:

`(z-z_2)/(z_1+z_2)= lambda_1 e^(i alpha)`........................(i)

`(z-z_3)/(z_1-z_3) =lambda _2 e^(i alpha)`.......................(ii)

(i) `div` (ii)

`(z-z_2)/(z_1-z_2) * (z_1-z_3)/(z-z_3) = lambda_1/lambda_2 =` Purely real.

`:. ((z-z_2)/(z-z_3)) ((z_1-z_3)/ (z_1-z_2))=( (bar z - bar z_2)/(bar z - bar z_3))((bar z_1 - bar z_3)/(bar z_1-bar z_2))`

The above equation represents a circle passing through `A(z_1), B(z_2)` and `C(z_3)`.
Q 2680178017

If `z_1 = 2 + 3 i , z_2 = 3 - 2 i` and `z_3 = - 1 - 2 sqrt 3 i` then which of the following is true?

(A)

`arg (z_3/z_2) =arg ((z_3-z_1)/(z_2-z_1))`

(B)

`arg (z_3/z_2) =arg (z_2/z_1)`

(C)

`arg (z_3/z_2) =2 arg((z_3-z_1)/(z_2-z_1))`

(D)

`arg(z_3/z_2) =1/2 arg ((z_3-z_1)/(z_2-z_1))`

Solution:

Note that `|z_1| =|z_2| =|z_3| = sqrt (13)`

Hence `z_ 1, z_2 , z _3 ` lies on a circle with centre `(0, 0)` and `r= sqrt 13` as shown

now `Arg z_2/z_3 = 2 Arg\ \ (z_2-z_1)/(z_3-z_1)`

`:. Arg z_3/z_2 =2 Arg \ \ (z_3-z_1)/(z_2-z_1)`
Correct Answer is `=>` (C) `arg (z_3/z_2) =2 arg((z_3-z_1)/(z_2-z_1))`

Imp. Note :

Let `z_1` and `z_2` be two given complex numbers and `z` be any complex number such that, `arg ((z-z_1)/(z-z_2))= alpha` where `alpha in (0, pi)`

Then `'z'` would be lie on an arc of segment of a circle on `z_1z_2` containing angle a. Clearly if `alpha in (0, pi/2), z` would lie on the major arc (excluding the points `z_1` and `z_2` ) and if `alpha in (pi/2 , pi). 'z'` would lie on the minor arc (excluding the points `z_1` and `z_2`)

Equation of a parabola in Complex Plane

(i) If `|z-z_0|= |(bar alpha z + alpha bar z+ b)/(2 |alpha|)` then locus of `z` is a parabola whose focus is `z_0` and directrix is the line `bar alpha z + alpha bar z + b=0` provided `bar alpha z_0 + alpha bar z_0 + b ne 0`





(ii) If `(z- bar z)^2 + 8a(z+ bar z)=0` then locus of `z` represents a parabola whose focus is `(a, 0)`, vertex is `(0, 0)` and real axis is the axis of parabola.

Put `z=x+iy`

`=> (i2y)^2 + 8a * 2x =0`

`=> -4y^2+ 16 ax =0`

`=> y^2=4ax`
Q 1187223187

The locus represented by the complex equation `|z−2−i|=|z|sin(π/4−arg⁡z)` is the part of

(A)

A pair of straight lines

(B)

A rectangle hyperbola

(C)

A circle

(D)

A parabola

Solution:

Let `z = x + iy = r ( cos θ + i sin θ )` then the equation is

`|(x−2)+i(y−1)|=r(1/sqrt2cos⁡θ−1/sqrt2sin⁡θ) `

`=1/sqrt2(rcos⁡θ−rsin⁡θ)`

or, `sqrt((x−2)^2+(y−1)^2)=1/sqrt2(x−y)`

Which is the part a parabola with focus `(2, 1)` and directrix `x - y = 0`
Correct Answer is `=>` (D) A parabola

Equation of an ellipse in Complex Plane

`|z-z_1|+ |z-z_2|=k`

(i) `k > |z_1-z_2|` then locus of `z` represents an ellipse whose foci are `z_1` and `z_2`





(ii) `k=|z_1-z_2|` then locus of `z` is line segment joining `z_1` and `z_2`.

`PS_1 + PS_2 =S_1 S_2 =|Z_1-z_2|=> P` lies on the line segment joining `S_1(z_ 1)` and `S_2(z_2)`.
Q 2650756614

If ` | z- 1 | + |z + 3| <= 8`, then the range of values of `|z- 4|` is

(A)

[0, 8]

(B)

[1, 8]

(C)

[1, 9]

(D)

[-3, 5]

Solution:

`A'` and `A` age the ` (-5,0)` and `(3,0)` respectively

min `| z - 4 | = A' P = 1 ` and max ` | z - 4 | = AP = 9`

` 1 <= | z - 4 | <= 9`
Correct Answer is `=>` (C) [1, 9]
Q 1117323289

The complex numbers satisfying `| z + 2 | + | z - 2 | = 8` and `| z - 6 | + | z + 6 | = 12` are

(This question may have multiple correct answers)

(A) `4`
(B) `- 4`
(C) `4i`
(D) `- 4i `
Solution:

The locus of `| z + 2 | - | z - 2 | = 8` is an ellipse having focii at `(2,0)` and `( - 2,0)` and length of major axis is `8` units.

i.e., `ae = 2` and `2a = 8`

`∴e=1/2, a=4`

Again the second equation represents a straight line segment such that its locus comprise of all points inside the segment from `( - 6,0)` to `(6,0)` as shown in the figure.
Correct Answer is `=>` (C)

Equation of a Hyperbola in Complex Plane

`||z-z_1|-|z-z_2||=k`



(ii) `k=|z_1-z_2|` then locus of `z` is union of two rays emanating from `z_1` and `z_2`.

`|PS_1-PS_2|= S_1S_2`

`||z-z_1|-|z-z_2|=|z_1-z_2|`

`:. P(z)` lies on the rays emanting either `z_1` or `z_2`

Examples

Solved examples
Q 1679734616

For any integer `k`, let `\alpha _{ k }=\cos \frac { k\pi }{ 7 } +i\sin\frac { k\pi }{ 7 } `, where `i=\sqrt { -1 }`. The value of the expression `\frac { \sum _{ k=1 }^{ 12 } | \alpha _{ k+1 } - \alpha _{ k }| }{ \sum _{ k=1 }^{ 3 } | \alpha _{ 4k-1 } - \alpha _{ 4k-2 }| }` is
JEE ADVANCED 2015
Solution:

`| \alpha_k - \alpha_{k+1} |` represents the side length of a 14 sided polygon (tetradecagon) inscribed in a unit circle.

Similarly, `|\alpha_{4k-1} - \alpha_{4k-2} | ` represents the side length of a 14 sided polygon inscribed in a unit circle.

Let l be the length of the side.

Hence, the required ratio `= frac{ 12 l}{3 l} =4`
Correct Answer is `=>` 4
Q 2251256124

Which of there represent a triangle
JEE Advanced Paper 2
(A)

`|z – 1| = |z – 2|`

(B)

`|z – 1| = |z – 2| = |z – i|`

(C)

`|z – 1| – |z – 2| = 2a`

(D)

`|z – 1|^2 + |z – 2|^2 = 4.`

Solution:

It represent 3 different non concurrent lines hence can represent a triangle
Correct Answer is `=>` (B) `|z – 1| = |z – 2| = |z – i|`
Q 1436656572

Let `A, B` and `C` represent the complex numbers `z_1, z_2, z_3` respectively on the complex plane. If the circumcentre of the triangle `ABC` lies at the origin, then the nine point centre is represented by the complex number

(A)

`(z_1+z_2)/2-z_3`

(B)

`(z_1+z_2-z_3)/2`

(C)

`(z_1+z_2+z_3)/2`

(D)

`(z_1-z_2-z_3)/2`

Solution:

Circumcentre `=0`, centriod `=(z_1+z_2+z_3)/3`

Let orthocentre be `gamma`

`:.` Centroid divides orthocentre and circumcentre as in the ratio `2: 1` (internally)

`(z_1 + z_2 + z_3)/3 = (1 · gamma + 2· 0)/(2+1)`

`:. gamma = z_1 + z_2 + z_3`

But nine point centre is the mid point of orthocentre and circum centre:·

`:.` Nine point centre `=(gamma+0)/2=(z_1+z_2+z_3)/2`
Correct Answer is `=>` (D) `(z_1-z_2-z_3)/2`
Q 1486845777

If the vertices of a triangle are `8 + 5i,- 3 + i,- 2- 3i` , the modulus and the argument of the complex number representing the centroid of this triangle respectively are

(A)

`2,pi/4`

(B)

`sqrt 2,pi/4`

(C)

`2 sqrt 2,pi/4`

(D)

`2 sqrt 2,pi/2`

Solution:

Centroid `=(8+5i-3+i-2-3i)/3`

`P`(say)`=1+i`

`|P|=sqrt(1+1)=sqrt 2`

`arg(P)=tan^(-1)(1//1)=pi/4`.
Correct Answer is `=>` (B) `sqrt 2,pi/4`
Q 2068334205

If `z = x + 3i` , then the value of `int_(2)^(4) [arg | (z-i)/(z+i)| ] dx` (where

`[*]` denotes the greatest integer function and `i = sqrt (-1)`, is

(A)

`3 sqrt(2)`

(B)

`6 sqrt(3)`

(C)

`sqrt (6)`

(D)

None of these

Solution:

`:. | (z-i)/(z+i) | = | (x+2i)/(x+4i) | = ( sqrt (x^2 +4) )/(sqrt (x^2 +16)) = ` purely real

`:. arg | (z-i) /(z+i) | =0` ` ( :.` imaginary part `= 0)`

`:. int_(2)^(4) [arg | (z-i)/(z+i) | ] dx= int_(2)^(4) [0] dx =0`
Correct Answer is `=>` (D) None of these
Q 2610467319



Assertion : If `A(z_1), B(z_2) , C(z_3)` are the vertices of an equilateral triangle `ABC`, then `arg ((z_2+z_3-2z_1)/(z_3-z_2))=pi/4`

Reason : If `angle B =alpha `, then `(z_1-z_2)/(z_3-z_2) = (AB)/(BC) e^(lnx)` or `arg((z_1-z_2)/(z_3-z_2))= alpha`

(A) Both A and R individually true and R is the correct explanation of A
(B) Both A and R are individually true but R is not the correct explanation of A
(C) A is true but R is false
(D) A is false but R is true
Solution:

`arg ((z_2=z_3-2z_1)/(z_3-z_2))= arg (((z_2+z_3)/2 -z_1)/(z_3-z_2))`

`pi/2 ` (as `AD bot BC`)
Correct Answer is `=>` (D)
Q 1446267173

If `X` be the set of all complex numbers `z` such that `| z | = 1`
and define relation `R` on `X` by `z_1 R z_2` is
`| arg z_1 - arg z_2| = 2n`, then `R` is

(A)

reflexive

(B)

symmetric

(C)

transitive

(D)

anti-symmetric

Solution:

`·:|z|=1, :. z=cos theta +i sin theta`

`:. arg (z) =theta`

Then `arg (z_1)=theta_1` and `arg (z_2) = theta_2`

`z_1 R z_2 <=> | arg z_1 - arg z_2 | =(2 pi)/3`

`<=> |theta_2 -theta_1| = 2 pi//3`

`<=> z_2 R z_1` but `z_1 ne z_2`

{if `z_1 = z_2` then `0 = 2pi//3` (impossible)}

`:.` Symmetric.
Correct Answer is `=>` (B) symmetric
Q 1412745639

If ` ((arg z_1)z_2)/((arg z_2)z_1)` IS a purely imaginary number, then ` |((arg z_1)z_2+(arg z_2)z_1)/((arg z_1)z_2-(arg z_2) z_1)|` is equal to

(A)

`0`

(B)

any real constant k

(C)

`1`

(D)

can't be determined

Solution:

Let `((arg z_2)z_1)/((arg z_1)z_2) = k*i`



By componendo and dividendo

`((arg z_2)z_1+(arg z_1)z_2)/((arg z_2) z_1-(arg z_1) z_2) = (ki+1)/(ki-1)= (1+ki)/-(1-ki)`

`:. |((arg z_2)z_1+(arg z_1)z_2)/((arg z_2)z_1-(arg z_1)z_2)|=|(1+ki)/(1-ki)|= sqrt(1+k^2)/sqrt(1+k^2)=1`
Correct Answer is `=>` (C) `1`
Q 2543180043

Let `z_1 = 10 + 6i, z_2 = 4 + 6i`, where `i = sqrt(-1)`. If `z` is
a complex number, such that the argument of `(z - z_1)// (z - z_2 )` is
`pi//4`, then prove that `| z - 7 - 9i | = 3 sqrt2`.

(A)

`sqrt2`

(B)

`7`

(C)

`9sqrt2`

(D)

` 3sqrt2`

Solution:

`∵ arg ( (z - z_1)/ (z - z_2 )) = pi/4`

It is clear that `z , z_1 , z_2` are non-collinear points.

Always a circle passes through `z, z_1` and `z_2`.

Let `z_0` be the centre of the circle.

On applying rotation theorem in `Delta BOC`,

`(z_1 - z_0)/(z_2 - z_0) = (OC)/(OB) e^(i pi//2) = i`

`=> (z_1 - z_0 ) = i (z_2 - z_0 )`

`=> 10 + 6i- z_0 = i (4 + 6i- z_0 )`

` => 16 + 2i = (1 - i) z_0`

or ` z_0 = ((16 + 2i))/((1 - i)) . ((1 + i))/((1 - i))`

` = (16 + 16i + 2i + 2i^2)/2`

`= (14 + 18i)/2 = 7 + 9i`

and radius,` r = OC = | z_0 - z_1 | = | 7 + 9i -10- 6i | = | -3 + 3i |`

`= sqrt(9 + 9) = 3 sqrt2`

Hence, required equation is

`| z - z_0 | = r`

`=> | z- 7- 9i | = 3sqrt2`
Correct Answer is `=>` (D) ` 3sqrt2`
Q 2036178072











Column IColumn II
(i) The polar form of `i + sqrt(3)` is (a) Perpendicular bisector of segment
joining `(-2, 0)` and `(2, 0)`.
(ii) The amplitude of `-1 + sqrt(-3)` is (b) On or outside the circle having
(iii) It `| z + 2 | = | z - 2 |` then locus of `z` is (c) `(2pi)/3`
(iv) It `| z + 2i | = | z - 2i |`, then locus of `z` is (d) Perpendicular bisectar of segment
joining `(0, - 2)` and `(0, 2)`
(v) Region represented by `| z + 4i | >= 3(e) `2( cos pi/6 + i sin pi/6)`
(vi) Region represented by `| z + 4| <=3` is (f) On or inside the circle having centre
`(- 4, 0)` and radius `3` units.
(vii) Conjugate of `(1 + 2i)/(1 - i)` lies in (g) First quadrant
(viii) Reciprocal of `1 - i` lies in (h) Third quadrant

NCERT Exemplar
Solution:

(i) Given, `z = i + sqrt(3) = r (cos theta + sin theta)`

` ∵ r cos theta = sqrt(3), rsin theta = 1`

` => r^2 =1 + 3 = 4 => r = 2 quad [∵ r > 0]`

` => tan alpha = |( rsin theta)/( r cos theta ) |= 1/sqrt(3)`

`=> tan alpha = 1/sqrt(3) => alpha = pi/6`

`∵ x > 0 , y > 0`

and ` arg (z) = theta = pi/6`

So the polar form of `z` is `2 (cos (pi/6) + i sin (pi/6))`.

(ii) Given that, `z = -1 + sqrt(-3) = - 1 + i sqrt(3)`

`:. tan alpha = |sqrt(3)/1 | = sqrt(3)`

` => tan alpha = tan (pi/3) => alpha = pi/3`

`∵ x < 0, y > 0`

`=> theta = pi - alpha = pi - pi/3 = (2pi)/3`

(iii) Given that, `| z+2 | = | z-2|`

` => | x + 2 + iy | = | x -2 + iy |`

` => (x + 2)^2 + y^2 = (x- 2)^2 + y^2`

` => x^2 + 4x + 4 = x^2 - 4x + 4 => 8x = 0`

` :. x = 0`

It is a straight line which is a perpendicular bisector of segment joining the points `(-2, 0)`
and `(2, 0)`.

(iv) Given that, `| z + 2i | = | z - 2i |`

` => | x + i (y + 2) | = | x + i(y-2)|`

` => x^2 + (y+ 2)^2 = x^2 + (y-2)^2`

`=> 4y = 0 => y = 0`

It is a straight line, which is a perpendicular bisector of segment joining `(0, -2)` and `(0, 2)`.

(v) Given that, `| z + 4i | >= 3 = | x + iy + 4i | >= 3`

`=> = | x + i (y + 4 ) | >= 3`

`=> sqrt(x^2 (y+ 4)^2) >= 3`

` => x^2 + (y + 4)^2 >= 9`

` = x^2 + y^2 + 8y + 16 >= 9`

` = x^2 + y^2 + 8y + 7 >= 0`

Which represent a circle. On or outside having centre `(0, - 4)` and radius `3`.

(vi) Given that, `| z + 4| <= 3`

`=> | x + iy + 4 | <= 3`

` => | x + 4 + iy | <= 3`

` => sqrt((x + 4)^2 + y^2 ) <= 3`

` => (x + 4)^2 + y^2 <= 9`

` => x^2 + 8x + 16 + y^2 <= 9`

`=> x^2 + 8x + y^2 + 7 <= 0`

It represent the region which is on or inside tile circle having the centre `(- 4, 0)` and radius `3`.

(vii)Given that, ` z = (1 + 2i)/(1-i) = ((1+ 2i) (1 + i))/((1-i)(1+i))`

` = (1+ 2i + i +2i^2)/(1 - i^2) = ( 1 - 2 + 3i)/(1+1) =( -1 + 3i)/2`

`:. z = (-1)/2 - (3i)/2`

Hence ` ((-1)/2 - (-3)/2)` lies in third quadrant.

(viii) Given that, ` z = 1 - i`

`:. 1/z = 1/(1-i) = (1 + i)/( (1 - i) (1 + i) ) = (1 + i) /(1-i^2) = 1/2 (1 + i)`

Hence,`( 1/2 , 1/2)` lies in first quadrant.
Correct Answer is `=>` ()
Q 2583078847

The point a' is the reflection of the point a in the line `z bar b + bar z b + c = 0`, if

(A)

`a' bar c + bar a b + c = 0`.

(B)

`a' bar b - bar a b + c = 0`.

(C)

`a' bar b + bar a b + c = 0`.

(D)

None of these

Solution:

Since, a' is the reflection of point a through the line.

So, the mid-point of `PQ`

i.e., `(a+a')/2 ` lies on `z bar b + bar z b + c = 0`

or ` barb ((a - a')/2) + b (( bar a + bar(a'))/2) + c= 0`

`=> bar b (a + a')+ b (bar a + bar (a') ) + 2c = 0` .......(i)

Since, `PQ bot AB`. Therefore,

Complex slope of `PQ +` Complex slope of `AB = 0`

`=> (a - a')/( bar a + bar(a')) + ( - b/bar b) = 0`

`=> bar b (a - a') - b (bar a - bar(a') )= 0` .....(ii)

On subtracting Eq. (ii) from Eq. (i), we get

`a' bar b + bar a b + c = 0`
Correct Answer is `=>` (C) `a' bar b + bar a b + c = 0`.
Q 2630667512



Assertion : If `z_1, z_2, z_3` are complex number representing the points `A, B, C` such that ` 2/z_1=1/z_2+1/z_3` Then circle through `A, B, C` passes through origin.

Reason : If `2z_2 = z_1+ z_3` then `z_1, z_2, z_3` are collinear.

(A) Both A and R individually true and R is the correct explanation of A
(B) Both A and R are individually true but R is not the correct explanation of A
(C) A is true but R is false
(D) A is false but R is true
Solution:

`2/z_1=1/z_2+ 1/z_3=> 1/z_1-1/z_2 =1/z_3 -1/z_1 => (z_2-z_1)/(z_1z_2)= (z_1-z_3)/(z_1z_3)`

`=> (z_2-z_1)/(z_3-z_1) =- z_2/z_3=> arg ((z_2-z_1)/(z_3-z_1))=arg (-z_2/z_3)`

`=> arg ((z_2-z_1)/(z_3-z_1))= pm pi+ arg (z_2/z_3) =pm pi + arg ((z_2-O)/(z_3-O))` (+ or - as applicable)

`=> ` Points `O, A, B, C` are concyclic.
Correct Answer is `=>` (B)
Q 2513878749

Inverse of a point a with respect to the cirde `| z- c | = R` (a and c are complex numbers, centre c and radius R ) is the point


(A)

` c `

(B)

` c + R^2/(bar a + bar c)`

(C)

` c + R^2/(bar a - bar c)`

(D)

None of these

Solution:

Let `a`' be the inverse point of a with respect to the circle

`| z- c | = R`, then by definition,

The points c, a, a' are collinear

We have, arg `(a'- c) = arg (a- c)`

`= - arg (bar a - bar c)`

`=> arg (a' - c) + arg (bar a - bar c) = 0`

`=> arg {(a'- c) (bar a - bar c)} =0`

`:. (a' - c) (bar a - bar c)` is purely real and positive.

By definition, `| a' - c | | a - c | = R^2`

`=> | a' - c | | bar a - bar c | = R^2`

`=> | (a'- c) (bar a- bar c) | = R_2`

`=> (a' - c) (bar a - bar c) = R_2` [ `∵ (a' -c) (bar a- bar c)` is purely real and positive]

` => a' - c = R^2/(bar a - bar c) => a' = c + R^2/(bar a - bar c)`
Correct Answer is `=>` (C) ` c + R^2/(bar a - bar c)`
Q 1406223178

Let `z_1 = 6 + i` and `z_2 = 4- 3i` . Let `z` be a complex number such that `arg ((z-z_1) /(z_2-z)) = pi/2` , then `z` sati.sfies

(A)

`|z-(5-i)|=5`

(B)

`|z-(5-i)|=sqrt5`

(C)

`|z-(5+i)|=5`

(D)

`|z-(5+i)|=sqrt 5`

Solution:

`arg ((z-z_1)/(z_2-z))=pi/2`

`:. z_1, z_2, z_3` lie on a circle.

`=> z_1` and `z_2` are the end points of diameter

`:.` centre `(z_0)=(z_1+z_2)/2`

`:. z_0=5-i`

and radius `=| z_1 - z_0 |`

`=|1 + 2i|`

`r=sqrt 5`

`:.` Equation circle is `| z - z_0 | = r`

or ` |z-(5-i)|=sqrt5`
Correct Answer is `=>` (B) `|z-(5-i)|=sqrt5`
Q 1476391276

If `z_1, z_2, z_3, z_4` are the four complex numbers represented
by the vertices of a quadrilateral taken in order such that
`z_1 - z_4 = z_2 - z_3` and amp `((z_4 - z_1)/(z_2-z_1)) = pi/2` , then the
quadrilateral is a

(This question may have multiple correct answers)

(A) rhombus
(B) square
(C) rectangle
(D) cyclic quadrilateral
Solution:

`amp ((z_4- z_1)/(z_2-z_1)) = pi/2`

but `z_1 - z_4 = z_2 - z_3`

and `z_3-z_4=z_2-z_1`

`amp(-(z_2-z_3)/(z_3-z_4))=pi/2`

`=> amp ((z_2-z_3)/(z_4-z_3))=pi/2`

`:. ABCD` is rectangle and cyclic quardilateral
Correct Answer is `=>` (C)
Q 1416880770

The distances of the roots of the equation
`| sin theta_1 | z^3 +| sin theta_2 | z^2 +| sintheta_3 | z +| sin theta_4 | = 3`, from
`z = 0`, are

(A)

greater than `2//3`

(B)

less than `2//3`

(C)

greater than `| sin theta_1| +| sin theta_2 | +| sin theta_3 | +| sin theta_4 |`

(D)

less than `|sin theta_1| + | sintheta_2|+| sin theta_3| +| sin theta_4 |`

Solution:

`·: | sin theta_1 | z^3 + | sin theta_2| z^2 + | sin theta_3 |z +| sin theta_4 | = 3`

`:. |3| =|| sin theta_1| z^3 +| sin theta_2| z^2 +| sin theta_3 | z+| sintheta_4 ||`

`:. sin theta_1|| z|^3 +| sin theta_2|| z |^2 +| sin theta_3 ||z|+ | sin theta_4 |`

`=> |z |^3 + | z |^2 + | z | + 1`

`le 1 +| z |+ | z |^2 + ... =`

`< 1+|z|+|z|^2+....oo`

`=1/(1-|z|)`

`=>1/3 > 1-|z|`

`=>|z| >2/3`

`:. |z-0| > 2/3`
Correct Answer is `=>` (A) greater than `2//3`
Q 1137812782

If `| z - 1 | + | z + 3 | ≤ 8`, then the range of values of `| z - 4 |` is

(A)

`[1,9]`

(B)

`(0,8)`

(C)

`[2,4]`

(D)

`(1,8)`

Solution:

∴ If `| z - 1 | + | z + 3 | ≤ 8`

`∴z` lies inside or on the ellipse whose foci an `(1,0)` and `( - 3,0)` and vertices are `( - 5,0)` and `(3,0).`

Clearly the minimum and maximum values of `|z−4| ` are `1` and `9` respectively, representing the distance PA and PA' . Thus , `1 ≤ |z−4| ≤ 9.`
Correct Answer is `=>` (A) `[1,9]`
Q 1476680576

Perimeter of the locus represented by `arg ( (z + i)/(z-i) ) = pi/4`,
(where `i = sqrt(-1)`) is equal to

(A)

`(3 pi)/2`

(B)

`(3 pi)/sqrt2`

(C)

`pi/sqrt 2`

(D)

None of these

Solution:

`·: angle QPR = pi // 4`

`:. angle QCR = pi// 2`, where `C` is centre of circle.

Now in `Delta QCR`,

`r^2 + r^2 = (QR)^2 =|2i |^2 = 4`

`r=sqrt 2`

`:.` Required parimeter `= 2pi r- 1/4 (2pi r)`

`3/2 pi r =3/2 pi (sqrt 2)=(3 pi)/(sqrt 2)`
Correct Answer is `=>` (B) `(3 pi)/sqrt2`
Q 1486367277

If `| z -1| +| z +3| le 8`, then the range of values of `| z- 4|,`
(where `i = R` ) is

(A)

`(0,7)`

(B)

`(1,8)`

(C)

`[1,9]`

(D)

`[2,5]`

Solution:

`|z-1|+|z+3| le 8`

`:.` `z` lies inside or on the ellipse whose foci are `(1, 0)` and `(- 3, 0)` and vertices are `(- 5, 0)` and `(3, 0)`

Now minimum and maximum value of `| z- 4|` are `1` and `9` respectively

`| z - 4| in [1, 9]`
Correct Answer is `=>` (C) `[1,9]`
Q 1187323287

P is a set consisting of those points which lie on the portion of a curve given by `arg((3z−6−3i)/(2z−8−6i))=π/4`, Q is a set consisting of those points which lie on the curve given by ` | z - 3 + i | = 3`, then

(This question may have multiple correct answers)

(A) `4+4/sqrt5+i(1−2/sqrt5)` is the complex number associated to both the sets
(B) Complex number z in the set Q for which `| | z - ( 2 + i ) | - | z - ( 4 + 3i ) | |` takes maximum value is `– i`
(C) None of these
(D) Complex number z in the set Q or which `| | z - ( 2 + i ) | - | z - ( 4 + 3i ) | |` takes minimum values are `(2+5/2i)` and `(3+5/2i)`
Solution:

Equation of `C_2`

`( x - 3 )^2 + ( y + 1)^2 = 9`

`x^2 + y^2 - 6x + 2y + 1 = 0` ..........(i)

For `C_1 , sin 45^0=sqrt(((3−2)^2+(2−1)^2)/r)`

`r=sqrt2sqrt2=2`

Centre (4,1)

Equation of curve `C_1 ( x - 4 )^2 + ( y - 1 )^2 = 4`

`⇒ x^2 + y^2 - 8x - 2y + 13 = 0`

Solving `C_1` and `C_2`

`2x + 4y - 12 = 0`

`x = 6 - 2y.`

Put value of x in (i) and after solving

`y=1−2/sqrt5x=4+4/sqrt5 `

Now, `| | z - ( 2 + i ) | - | z - ( 4 + 3i ) | |` will take maximum value

if `z, 2 + i ,4 + 3i ` are collinear.

Equation of line joining `( 2 + i )` and `( 4 + 3i )` is `y - 1 = 1 ( x - 2 )`

`⇒ x - y - 1 = 0`

Intersection of `x - y - 1 = 0` with `C_2 ( x - 3 )^2 + ( x - 1 + 1 )^2 = 9`

`⇒ x = 3, 0`

`x = 0 ⇒ y = - 1`

Also, the point will lie on `C_2` and on the line which is perpendicular bisector of line joining `(2,1)` and `(4,3)` then the value will be zero.

One of the possible value is `x < 3, y = 2`
Correct Answer is `=>` (A)
Q 1167123085

one vertex of the triangle of maximum area that can be inscribed in the curve `|z−(1+i)|=2sqrt2` is `−2+2i` then the remaining vertices are

(A)

`((5+sqrt3)/2)+i((1+3sqrt3)/2)`

(B)

`((5−sqrt3)/2)+i((1+3sqrt3)/2)`

(C)

`((5−sqrt3)/2)+i(((1−3sqrt3)/2)`

(D)

`((5+sqrt3)/2)+i((1−3sqrt3)/2)`

Solution:

`arg((z_2−z_0)/(z_1−z_0))=(2π)/3⇒arg((z_2−(1+i))/(−3+i))=(2π)/3 `

`⇒z_2−(1+i)=e^(i2π//3)(−3+i)`

`⇒z_2=((−1=isqrt3)/2)(−3=i)+1+i `

`=((−1+isqrt3)(−3+i)+2+2i)/2 `

`⇒z_2=((5−sqrt3)+i(1−3sqrt3))/2`

Also `arg((z_3−z_0)/(z_1−z_0))=−(2π)/3`

`z_3=e^(−2π//3)(−3+i)+(1+i) `

`z_3=−((1+isqrt3)/2)(−3+i)+(1+i) `

`=−(((−3−sqrt3)-i(1−3sqrt3))+2(1+0))/2 `

`z_3=((5+sqrt3)+i(1+3sqrt3))/2`
Correct Answer is `=>` (A)
Q 1157112984

If points A and B are represented by the non - zero complex numbers `z_1` and `z_2` on the Argand plane such that `| z_1 + z_2 | = | z_1 - z_2 | ` and O is the origin, then

(This question may have multiple correct answers)

(A) ∆OAB is isosceles
(B) `arg(z_1/z_2)=±π/2`
(C) Circumcentre of ∆OAB is `(z_1−z_2)/2`
(D) Orthocentre of ∆OAB lies at O
Solution:

`| z_1 + z_2 | = | z_1 - z_2 |`

`⇒(z_1+z_2)(barz_1+barz_2=(z_1−z_2)(barz_1−barz_2)`

`⇒ z_1 z_2 +z_2barz_1=0`

`⇒z_1/z_2=−((barz_1)/z_2)⇒z_1/z_2` is purely imaginary

Also from (i) `| z_1 - z_2 |^2 = | z_1 |^2 + | z_2 |^2`

⇒ ∆OAB is a right angled triangle ,right angled at O. So circumcentre `=(z_1+z_2)/2`.

Orthocentre of ∆OAB lies at O, Circumcentre of ∆OAB is `(z_1−z_2)/2
, arg(z_1/z_2)=±π/2`
Correct Answer is `=>` (B)
Q 2610691519








Column IColumn II
(A) Locus of the point `z` satisfying the equation `Re(z^2) =Re (z+ bar z)` (1) A Parabola
(B) Locus of the point `z` satisfying the equation `|z-z_1| +|z-z_2| = lambda, lambda in R^(+)` and `lambda ≮ |z_1-z_2|` (2) A straight line
(C) Locus of the point z satisfying the equation `|(2 z-i)/(z+1)|=m` where `i= sqrt(-1)` and `m in R^+` (3) An ellipse
(D) If `| bar z|=25` then the points representing the complex number `-1 + 75 bar z` will be a (4) A rectangular hyperbola
(5) A circle


(A)

`A-> 4, quad B-> (2,3), quad C->(2,5), quad D->5`

(B)

`A-> 5, quad B-> (2,3), quad C->(2,5), quad D->4`

(C)

`A-> 4, quad B-> 5, quad C->2, quad D->3`

(D)

`A-> (2,3), quad B-> 4, quad C->(2,5), quad D->5`

Solution:

(1) Put `z = x + iy`

`:. Re(x + iy)^2 = Re(x + iy + x - iy)`

`x^2- y^2 = 2x`

or `x^2 - y^2 - 2x = 0`

Rectangular hyperbola, eccentricity `= sqrt 2`

(2) For ellipse `lambda > |z_1 -z_2| ` and for straight line

`lambda=|z_1-z_2|`

(3) `|(2z-i)/(z+i)|=m`

`=> |(z-i/2)/(z+1)| =m/2`

for `m=2 , |(z-i/2)/(z+1)| =1`

`=> |z-i/2| =|z+1|`

ie, a straight line and for `m ne 2`, locus is circle

(4) Let `z=iy`

`=> x^2 +y^2=25^2`

`-1 + 75 bar z =75 -1 + i 75 y =h+ik`

`=> ((h+1)/75)^2 +(k/75)^2=25^2`

`=>` Locus of `(h, k)` is a circle
Correct Answer is `=>` (A) `A-> 4, quad B-> (2,3), quad C->(2,5), quad D->5`
Q 2680756617

If ` ( z - (1 + i))/(z + (1 - i))` is pure imaginary, then z lies on

(A)

a straight line

(B)

a cricle

(C)

a line segment

(D)

None of these

Solution:

If ` ( z - (1 + i))/(z + (1 - i))` is pure imaginary` => ( z - (1 + i))/(z + (1 - i)) + (bar z - (1 - i))/(bar z + (1 - i)) = 0`

`=> z bar z + z(1- i) - bar z(1 + i)- 2 + z bar z (1 - i) bar z + (1 + i) bar z- 2 = 0`

`=> z bar z = 2`

`:. z` lies on a circle
Correct Answer is `=>` (B) a cricle
Q 2543180043

Let `z_1 = 10 + 6i, z_2 = 4 + 6i`, where `i = sqrt(-1)`. If `z` is
a complex number, such that the argument of `(z - z_1)// (z - z_2 )` is
`pi//4`, then prove that `| z - 7 - 9i | = 3 sqrt2`.

(A)

`sqrt2`

(B)

`7`

(C)

`9sqrt2`

(D)

` 3sqrt2`

Solution:

`∵ arg ( (z - z_1)/ (z - z_2 )) = pi/4`

It is clear that `z , z_1 , z_2` are non-collinear points.

Always a circle passes through `z, z_1` and `z_2`.

Let `z_0` be the centre of the circle.

On applying rotation theorem in `Delta BOC`,

`(z_1 - z_0)/(z_2 - z_0) = (OC)/(OB) e^(i pi//2) = i`

`=> (z_1 - z_0 ) = i (z_2 - z_0 )`

`=> 10 + 6i- z_0 = i (4 + 6i- z_0 )`

` => 16 + 2i = (1 - i) z_0`

or ` z_0 = ((16 + 2i))/((1 - i)) . ((1 + i))/((1 - i))`

` = (16 + 16i + 2i + 2i^2)/2`

`= (14 + 18i)/2 = 7 + 9i`

and radius,` r = OC = | z_0 - z_1 | = | 7 + 9i -10- 6i | = | -3 + 3i |`

`= sqrt(9 + 9) = 3 sqrt2`

Hence, required equation is

`| z - z_0 | = r`

`=> | z- 7- 9i | = 3sqrt2`
Correct Answer is `=>` (D) ` 3sqrt2`
Q 2600656518

Let S denote the set of all complex numbers z satisfying the inequality ` | z - 5i | <= 3`. The complex numbers `z` in S having least positive argument is :

(A)

` ( 12 - 16 i)/5`

(B)

` ( 12 + 16 i)/5`

(C)

` ( 16 - 12 i)/5`

(D)

` ( 12 + 16 i)/5`

Solution:

See the figure

`| z - 5 | <= 3`

the point is `(4 cos theta, 4 sin theta)`

` ( 4 . 3/4 , 4 . 4/5) => ( ( 12 + 16 i)/5)`
Correct Answer is `=>` (D) ` ( 12 + 16 i)/5`
Q 2610691519








Column IColumn II
(A) Locus of the point `z` satisfying the equation `Re(z^2) =Re (z+ bar z)` (1) A Parabola
(B) Locus of the point `z` satisfying the equation `|z-z_1| +|z-z_2| = lambda, lambda in R^(+)` and `lambda ≮ |z_1-z_2|` (2) A straight line
(C) Locus of the point z satisfying the equation `|(2 z-i)/(z+1)|=m` where `i= sqrt(-1)` and `m in R^+` (3) An ellipse
(D) If `| bar z|=25` then the points representing the complex number `-1 + 75 bar z` will be a (4) A rectangular hyperbola
(5) A circle


(A)

`A-> 4, quad B-> (2,3), quad C->(2,5), quad D->5`

(B)

`A-> 5, quad B-> (2,3), quad C->(2,5), quad D->4`

(C)

`A-> 4, quad B-> 5, quad C->2, quad D->3`

(D)

`A-> (2,3), quad B-> 4, quad C->(2,5), quad D->5`

Solution:

(1) Put `z = x + iy`

`:. Re(x + iy)^2 = Re(x + iy + x - iy)`

`x^2- y^2 = 2x`

or `x^2 - y^2 - 2x = 0`

Rectangular hyperbola, eccentricity `= sqrt 2`

(2) For ellipse `lambda > |z_1 -z_2| ` and for straight line

`lambda=|z_1-z_2|`

(3) `|(2z-i)/(z+i)|=m`

`=> |(z-i/2)/(z+1)| =m/2`

for `m=2 , |(z-i/2)/(z+1)| =1`

`=> |z-i/2| =|z+1|`

ie, a straight line and for `m ne 2`, locus is circle

(4) Let `z=iy`

`=> x^2 +y^2=25^2`

`-1 + 75 bar z =75 -1 + i 75 y =h+ik`

`=> ((h+1)/75)^2 +(k/75)^2=25^2`

`=>` Locus of `(h, k)` is a circle
Correct Answer is `=>` (A) `A-> 4, quad B-> (2,3), quad C->(2,5), quad D->5`
Q 2670091816

Match the column if `|(z_1z-z_2)/(z_1z+z_2)|=k, (z,z_2 ne 0)` then locus of `z` is






Column IColumn II
(A) `k = 1` (P) line segment
(B) `k = 0` (Q) Parabola
(C) `k notin (0,1)` (R) point
(D) `k=2` (S) straight line
(T) circle


(A)

`A-> q, quad B-> r, quad C->s, quad D->t`

(B)

`A-> t, quad B-> r, quad C->t, quad D->s`

(C)

`A-> s, quad B-> r, quad C->t, quad D->t`

(D)

`A-> t, quad B-> r, quad C->s, quad D->t`

Solution:

`|(z_1z-z_2)/(z_1z+z_2) |=k => | (z-z_2/z_1)/(z+z_2/z_1) |=k`

Clearly if `k ne 0, 1`, then `z` would lie on a circle

If `k = 1, z` would lie on a perpendicular bisector of the line segment joining `z_2/z_1` and `(-z_2)/z_1`

If `k = 0, z` represents a point.
Correct Answer is `=>` (C) `A-> s, quad B-> r, quad C->t, quad D->t`
Q 2610467310

If perimeter of the locus represented by arg ` ((z+ i)/(z-i)) = pi/4` (where ` i = sqrt(-1) ` ) is ` k` then find the value of ` (2k^2)/pi^2`

(A)

3

(B)

9

(C)

27

(D)

-9

Solution:

`r^2 + r^2 = 4 => r = sqrt2`

read perimeter `= 3/2 pi r = (3pi)/sqrt2 = k`

`=> (2k^2)/pi^2 = 9` Ans.
Correct Answer is `=>` (B) 9
Q 1466323275

The locus of `z` which satisfies the inequality `log_(0.3) | z- 1| > log_(0.3) | z- i |` is given by

(A)

`x+y <0`

(B)

`x+y >0`

(C)

`x-y >0`

(D)

`x-y <0`

Solution:

`log_(0.3) | z -1| > log_(0.3) | z - i |`

`=> |z-1| < |z-i|`

`=> | z -1|^2 <| z- i |^2`

`=> (z -1)(bar z -1) < (z -i)(bar z + i)`

`=> z bar z - z -bar z + 1 < z bar z + iz - i bar z + 1`

`=> (1+i)z+(1-i) bar z > 0`

`=> (z +bar z) + i (z -bar z) > 0`

`=> ((z+ bar z)/2)-((z- bar z)/(2i)) > 0` (If `z=x+iy`)

`=> x-y >0`
Correct Answer is `=>` (C) `x-y >0`
Q 1659534414

lf `z` is any complex number satisfying `|z-3-2i|\leq 2`, then the minimum value of `|2z -6+5i|` is :
JEE ADVANCED 2011
Solution:

Given,`| z-3-2i | \le 2`

`| z-(3+2i) | \le 2`

This is a circle with centre (3,2) and radius 2.This represents the points inside and on the circle. The circle touches the X-axis

Now, `| 2z-6+5i | =2| z-3+\frac { 5i }{ 2 } \|`

=`2| z-(3-\frac { 5i }{ 2 } ) |`

So, for minimum value, this vertical distance should be ` \frac{5}{2}`

So, minimum value of `| 2z-6+5i | = 2\times \frac { 5 }{ 2 } =5`
Correct Answer is `=>` 5
 
SiteLock