(1) `tan^(-1) x +tan^(-1) y`
`= { tt (( tan^-1 ((x+y)/(1-xy)) , if xy < 1 ) , (pi+tan^(-1) ((x+y)/(1-xy)) , if x > 0 text(,) y > 0 text(,) xy > 1 ) , (-pi + tan^(-1) ((x+y)/(1-xy)) , if x < 0 text(,) y < 0 text(,) xy > 1))`
(2) `tan^(-1)x -tan^(-1)y = tan^(-1) ((x-y)/(1+xy))` If ` xy > -1 ` (with no other restriction)
(3) `tan^(-1) x+tan^(-1)y+tan^(-1)z`
` = tan^(-1) [ (x+y+z-xyz)/(1-(xy+yz+zx))]`
( where `x > 0 , y > 0 , z > 0` and `xy+yz+zx < 1` and `xy < 1 , yz < 1 , zx < 1`)
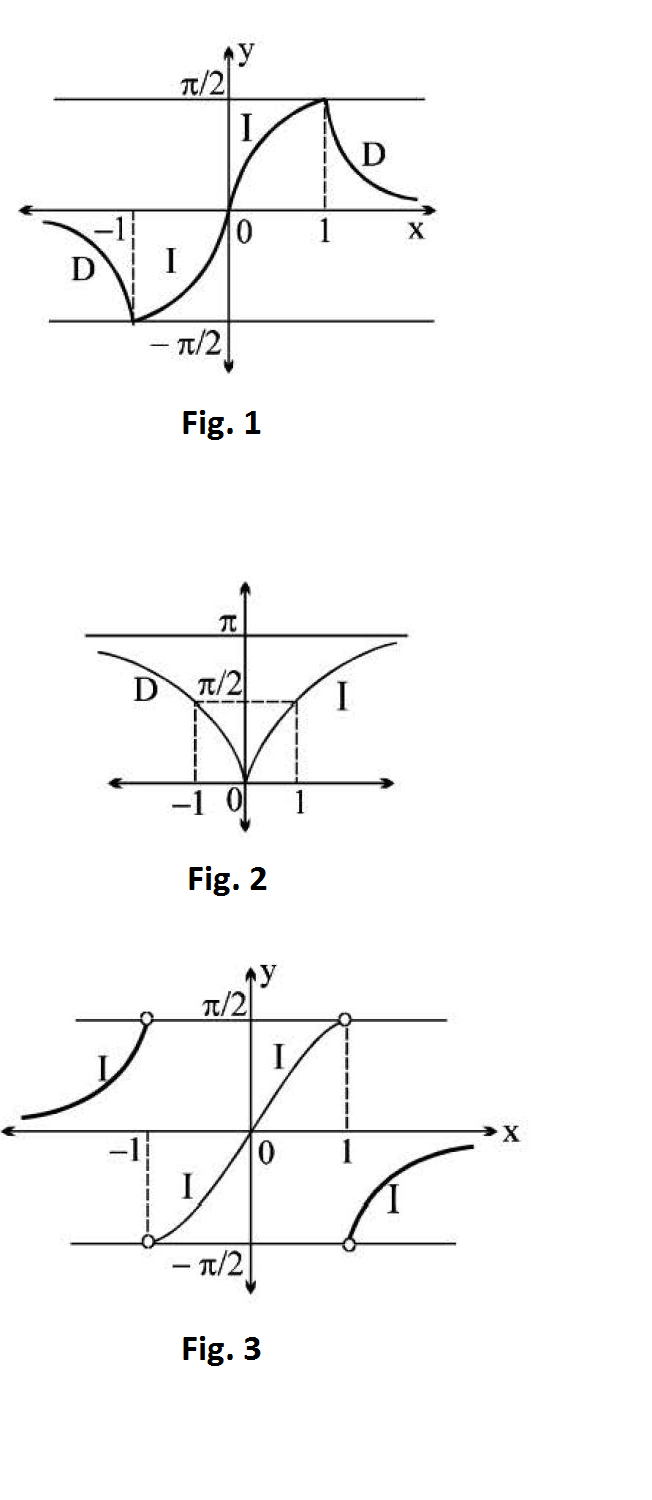
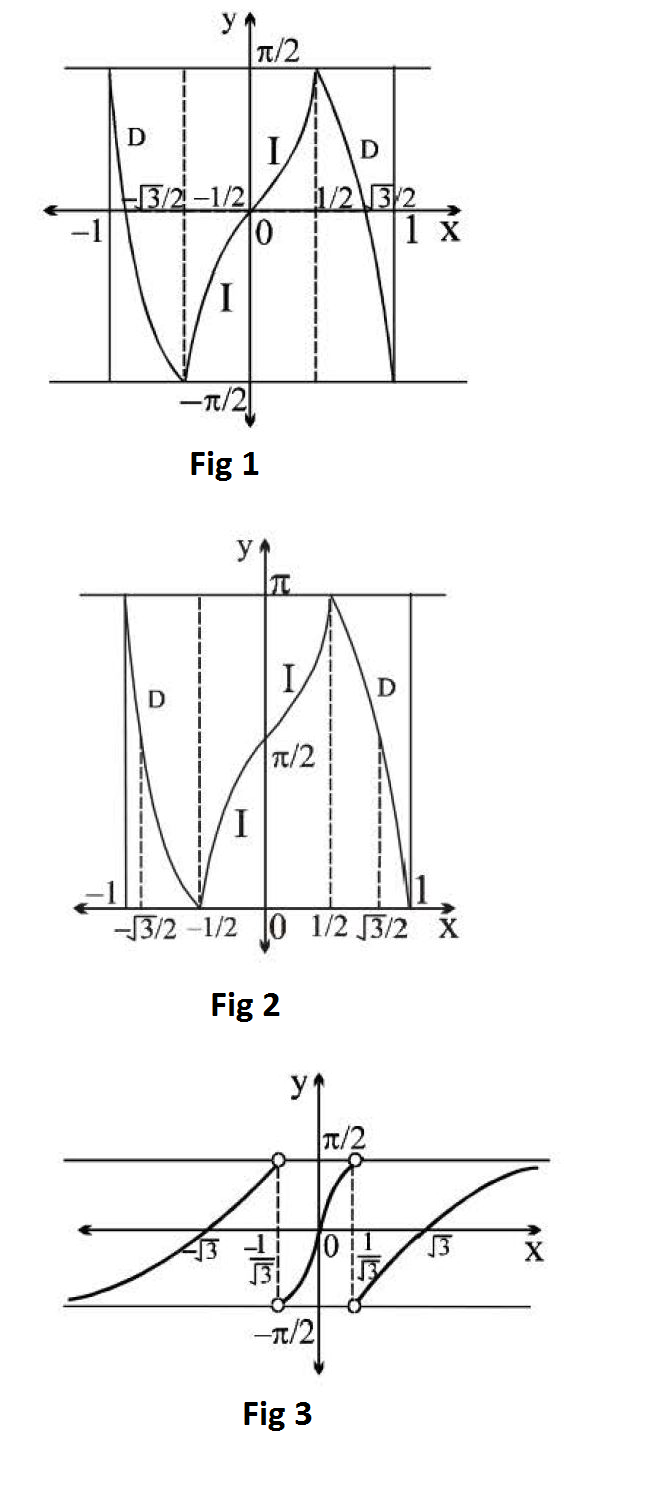
Proof of (`I`): Let `tan^(-1) x = A` and `tan^(-1)y = B` where `A , B ∈ ( -pi/2 , pi/2)`
Now `tan(A+B) = (tanA+tanB)/(1-tanAtanB) = (x+y)/(1-xy)`
`=> tan^(-1)((x+y)/(1-xy)) = tan^(-1) tan(A+B)`
` = tan^(-1) tanalpha` where `alpha ∈ (-pi , pi)`
`tan^(-1) (( x+y)/(1-xy)) = tan^(-1) (tanalpha)`
` = { tt (( alpha+pi , -pi < alpha < -pi/2) , (alpha , -pi/2 le alpha le pi/2) , (alpha-pi , pi/2 < alpha < pi )) = { tt ((tan^(-1) x+tan^(-1)y+pi , -pi < tan^(-1) x+tan^(-1)y < -pi/2) , (tan^(-1)x+tan^(-1)y , -pi/2 le tan^(-1) x+tan^(-1)y le pi/2) , (tan^(-1) x+tan^(-1)y - pi , pi/2 < tan^(-1)x+tan^(-1)y < pi))`
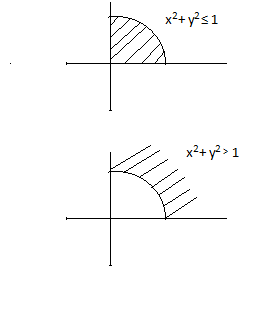
Case -I : `-pi < tan^(-1) x +tan^(-1)y < -pi/2 => x < 0 , y < 0`
Also `tan^(-1) x < -pi/2 - tan^(-1)y`
`=> tan^(-1)x < - (pi/2 - tan^(-1) (-y) ) => x < - (-1/y) => x < 1/y => xy > 1`
Case - II : `pi/2 < tan^(-1)x +tan^(-1) y < pi => x , y > 0`
Also `tan^(-1) x > pi/2 - tan^(-1) y => tan^(-1) x > tan^(-1) \ \ 1/y => x > 1/y => xy > 1`
Case- III : `-pi/2 le tan^(-1)x +tan^(-1)y le pi/2 => xy < 1`
(1) `tan^(-1) x +tan^(-1) y`
`= { tt (( tan^-1 ((x+y)/(1-xy)) , if xy < 1 ) , (pi+tan^(-1) ((x+y)/(1-xy)) , if x > 0 text(,) y > 0 text(,) xy > 1 ) , (-pi + tan^(-1) ((x+y)/(1-xy)) , if x < 0 text(,) y < 0 text(,) xy > 1))`
(2) `tan^(-1)x -tan^(-1)y = tan^(-1) ((x-y)/(1+xy))` If ` xy > -1 ` (with no other restriction)
(3) `tan^(-1) x+tan^(-1)y+tan^(-1)z`
` = tan^(-1) [ (x+y+z-xyz)/(1-(xy+yz+zx))]`
( where `x > 0 , y > 0 , z > 0` and `xy+yz+zx < 1` and `xy < 1 , yz < 1 , zx < 1`)
Proof of (`I`): Let `tan^(-1) x = A` and `tan^(-1)y = B` where `A , B ∈ ( -pi/2 , pi/2)`
Now `tan(A+B) = (tanA+tanB)/(1-tanAtanB) = (x+y)/(1-xy)`
`=> tan^(-1)((x+y)/(1-xy)) = tan^(-1) tan(A+B)`
` = tan^(-1) tanalpha` where `alpha ∈ (-pi , pi)`
`tan^(-1) (( x+y)/(1-xy)) = tan^(-1) (tanalpha)`
` = { tt (( alpha+pi , -pi < alpha < -pi/2) , (alpha , -pi/2 le alpha le pi/2) , (alpha-pi , pi/2 < alpha < pi )) = { tt ((tan^(-1) x+tan^(-1)y+pi , -pi < tan^(-1) x+tan^(-1)y < -pi/2) , (tan^(-1)x+tan^(-1)y , -pi/2 le tan^(-1) x+tan^(-1)y le pi/2) , (tan^(-1) x+tan^(-1)y - pi , pi/2 < tan^(-1)x+tan^(-1)y < pi))`
Case -I : `-pi < tan^(-1) x +tan^(-1)y < -pi/2 => x < 0 , y < 0`
Also `tan^(-1) x < -pi/2 - tan^(-1)y`
`=> tan^(-1)x < - (pi/2 - tan^(-1) (-y) ) => x < - (-1/y) => x < 1/y => xy > 1`
Case - II : `pi/2 < tan^(-1)x +tan^(-1) y < pi => x , y > 0`
Also `tan^(-1) x > pi/2 - tan^(-1) y => tan^(-1) x > tan^(-1) \ \ 1/y => x > 1/y => xy > 1`
Case- III : `-pi/2 le tan^(-1)x +tan^(-1)y le pi/2 => xy < 1`
 The value of `tan^(-1) sqrt((a(a+b+c))/(bc))+ tan^(-1) sqrt((b(a+b+c))/(ca))+ tan^(-1) sqrt((c(a+b+c))/(ab))` is equal to
The value of `tan^(-1) sqrt((a(a+b+c))/(bc))+ tan^(-1) sqrt((b(a+b+c))/(ca))+ tan^(-1) sqrt((c(a+b+c))/(ab))` is equal to