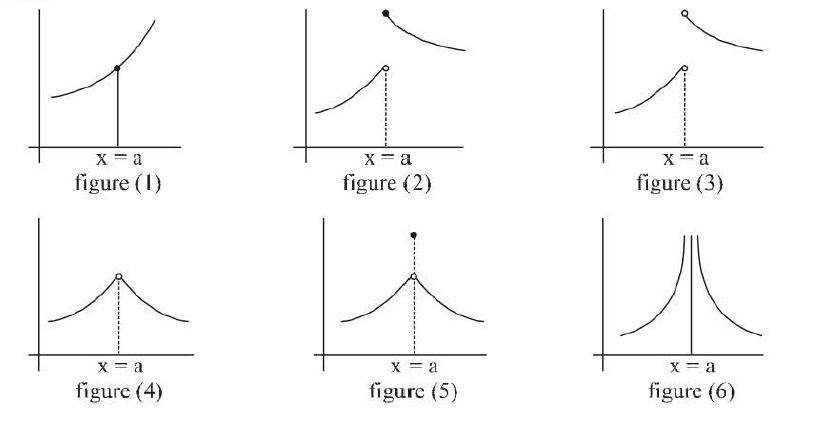
`"1. Removable Discontinuity :"`
Here `lim_(x->a) f(x)` necessarily exists, but is either not equal to `f(a)` or `f(a)` is not defined. In this case, therefore it is possible to redefine the function in such a manner that `Lim_(x-.a) f(x) =f(a)` and thus making the function continuous. These discontinuities can be further classified as :
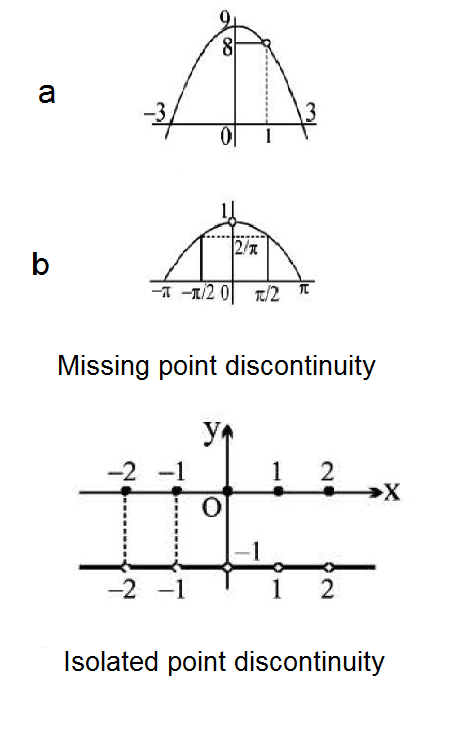
(A) Missing point discontinuity :
Here `Lim_(x->a) f(x)` exists. But `f(a)` is not defined.
(a) `f(x) =( ((x-1) (9-x^2) )/(x-1) ) x ne 1`
at `x = 1, f(1)` is not defined. Hence `f(x)` has missing point of discontinuity at `x = 1`.
(b) `f(x) =(sin x)/x , x ne 0`
`f(0)` is not defined. `f(x)` has missing point of discontinuity at `x = 0`.
(B) Isolated point discontinuity :
Here `Lim_(x->a) f(x) ` exists, also `f(a)` is defined but `Lim_(x->a) f(x) ne f(a)`
(a) `f(x) = [x] + [-x] = [ tt ( (0, text(if) x in I) , (-1 , text(if) x notin I) )`
has isolated point of discontinuity at all integeral points.
`"2 . Non -Removable Discontinuity :"`
- Here `Lim_(x->a) f(x)` does not exists and therefore it is not possible to redefine the function in any manner to
make it continuous. Such discontinuities can be further classified into 3 fold.
(a) Finite type (both limits finite and unequal) :
(i) `Lim_(x->0) tan^(-1) (1/x)= [tt( (f(0^+) =pi/2) , ( f(0^-) = - pi/2) )` ; jump `= pi`
(ii) `Lim_(x->0) (|sin x |/x)= [tt( (f(0^+) =1) , ( f(0^-) = - 1) )` ; jump `= 2`
(b) Infinite type (at least one of the two limit are infinity) : (i) `f(x) = (x/(1-x))` at `x=1 ,[tt( (f(1^+) =-oo) , ( f(1^-) = + oo) )`
(i) `f(x) = 2^(tanx)` at `x=pi/2 ,[tt( (f((pi/2)^+) =0) , ( f((pi/2)^-) = oo) )`
(c) Oscillatory (limits oscillate between two finite quantities) : (i) ` tt ( (f(x) =sin( 1/x) ) ,( text (or)) ,( f(x) =cos (1/x)) ) ]` at `x=0` oscillates between `- 1` & `1`
`"1. Removable Discontinuity :"`
Here `lim_(x->a) f(x)` necessarily exists, but is either not equal to `f(a)` or `f(a)` is not defined. In this case, therefore it is possible to redefine the function in such a manner that `Lim_(x-.a) f(x) =f(a)` and thus making the function continuous. These discontinuities can be further classified as :
(A) Missing point discontinuity :
Here `Lim_(x->a) f(x)` exists. But `f(a)` is not defined.
(a) `f(x) =( ((x-1) (9-x^2) )/(x-1) ) x ne 1`
at `x = 1, f(1)` is not defined. Hence `f(x)` has missing point of discontinuity at `x = 1`.
(b) `f(x) =(sin x)/x , x ne 0`
`f(0)` is not defined. `f(x)` has missing point of discontinuity at `x = 0`.
(B) Isolated point discontinuity :
Here `Lim_(x->a) f(x) ` exists, also `f(a)` is defined but `Lim_(x->a) f(x) ne f(a)`
(a) `f(x) = [x] + [-x] = [ tt ( (0, text(if) x in I) , (-1 , text(if) x notin I) )`
has isolated point of discontinuity at all integeral points.
`"2 . Non -Removable Discontinuity :"`
- Here `Lim_(x->a) f(x)` does not exists and therefore it is not possible to redefine the function in any manner to
make it continuous. Such discontinuities can be further classified into 3 fold.
(a) Finite type (both limits finite and unequal) :
(i) `Lim_(x->0) tan^(-1) (1/x)= [tt( (f(0^+) =pi/2) , ( f(0^-) = - pi/2) )` ; jump `= pi`
(ii) `Lim_(x->0) (|sin x |/x)= [tt( (f(0^+) =1) , ( f(0^-) = - 1) )` ; jump `= 2`
(b) Infinite type (at least one of the two limit are infinity) : (i) `f(x) = (x/(1-x))` at `x=1 ,[tt( (f(1^+) =-oo) , ( f(1^-) = + oo) )`
(i) `f(x) = 2^(tanx)` at `x=pi/2 ,[tt( (f((pi/2)^+) =0) , ( f((pi/2)^-) = oo) )`
(c) Oscillatory (limits oscillate between two finite quantities) : (i) ` tt ( (f(x) =sin( 1/x) ) ,( text (or)) ,( f(x) =cos (1/x)) ) ]` at `x=0` oscillates between `- 1` & `1`