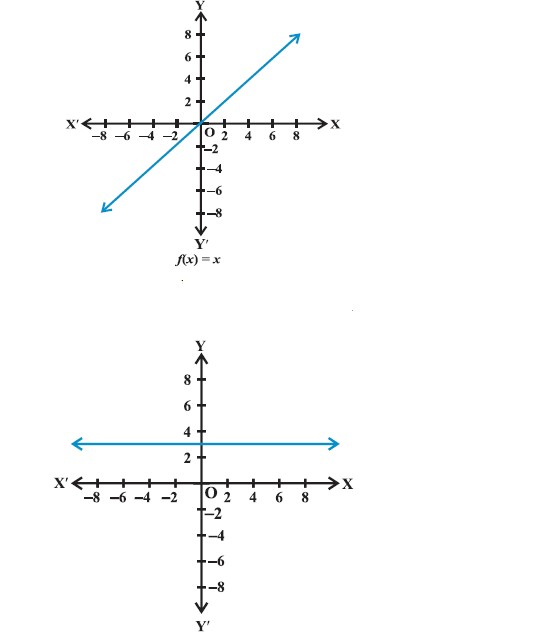
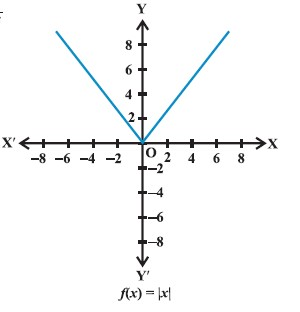
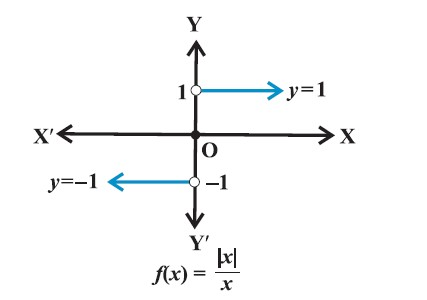
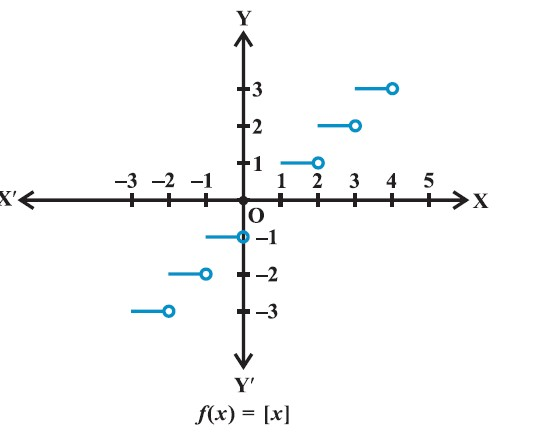
Function :

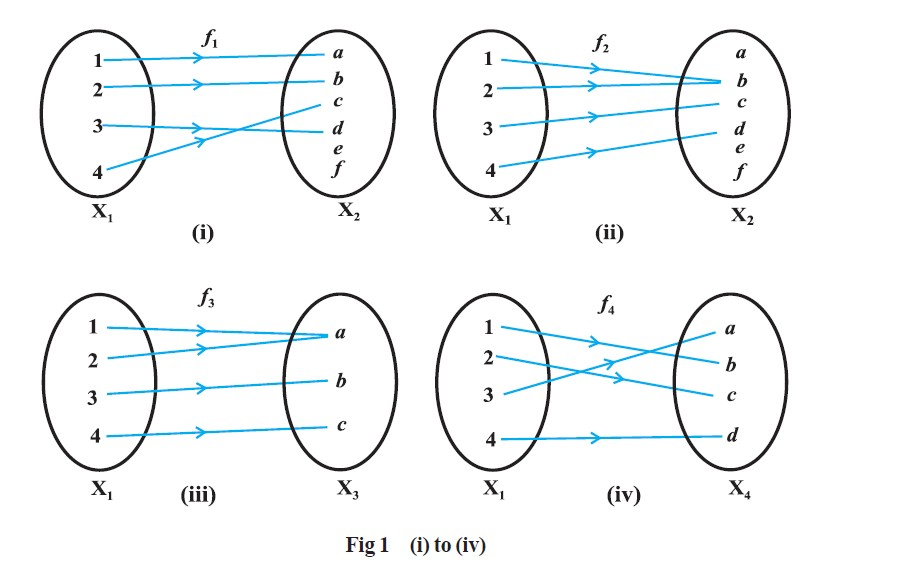
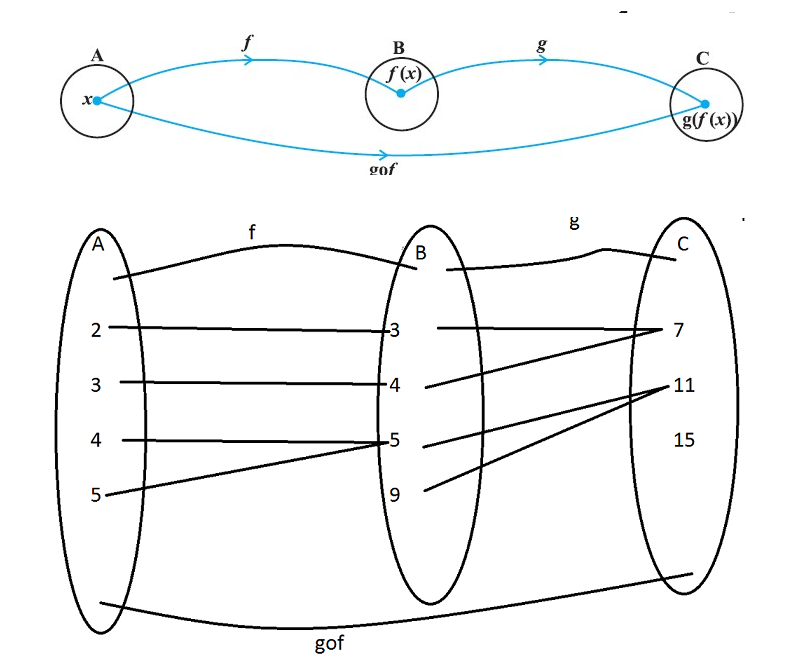
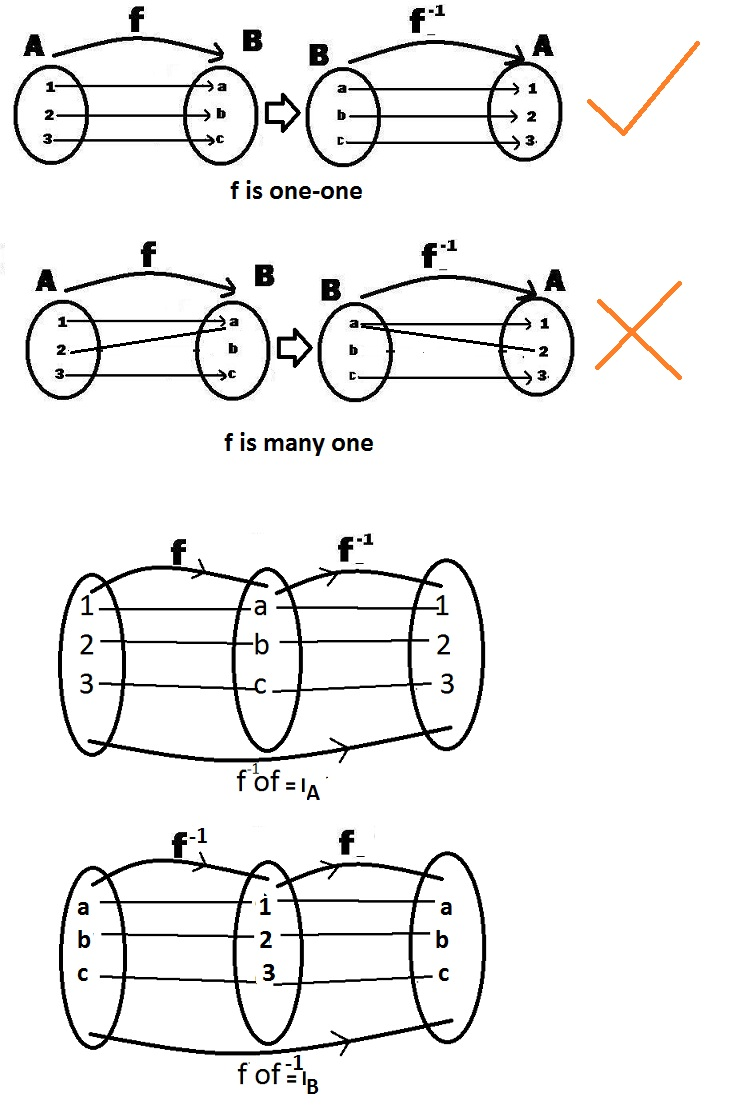
Definition : A relation f from a set A to a set B is said to be a function if every element of set A has one and only one image in set B.
- In other words, a function f is a relation from a non-empty set A to a non-empty set B such that the domain of f is A and no two distinct ordered pairs in f have the same first element.
- A function is a special relationship where each input has a single output.
- It is often written as `"f(x)"` where x is the input value.
Example: `f(x) = x/2` (`"f` of `x` is `x` divided by `2"`) is a function, because each input `"x"` has a single output `"x/2"`:
• `f(2) = 1`
• `f(−10) = −5`
- In other words, a function f is a relation from a non-empty set A to a non-empty set B such that the domain of f is A and no two distinct ordered pairs in f have the same first element.
- A function is a special relationship where each input has a single output.
- It is often written as `"f(x)"` where x is the input value.
Example: `f(x) = x/2` (`"f` of `x` is `x` divided by `2"`) is a function, because each input `"x"` has a single output `"x/2"`:
• `f(2) = 1`
• `f(−10) = −5`