Slope of a Line
Inclination of a Line `(theta) :`
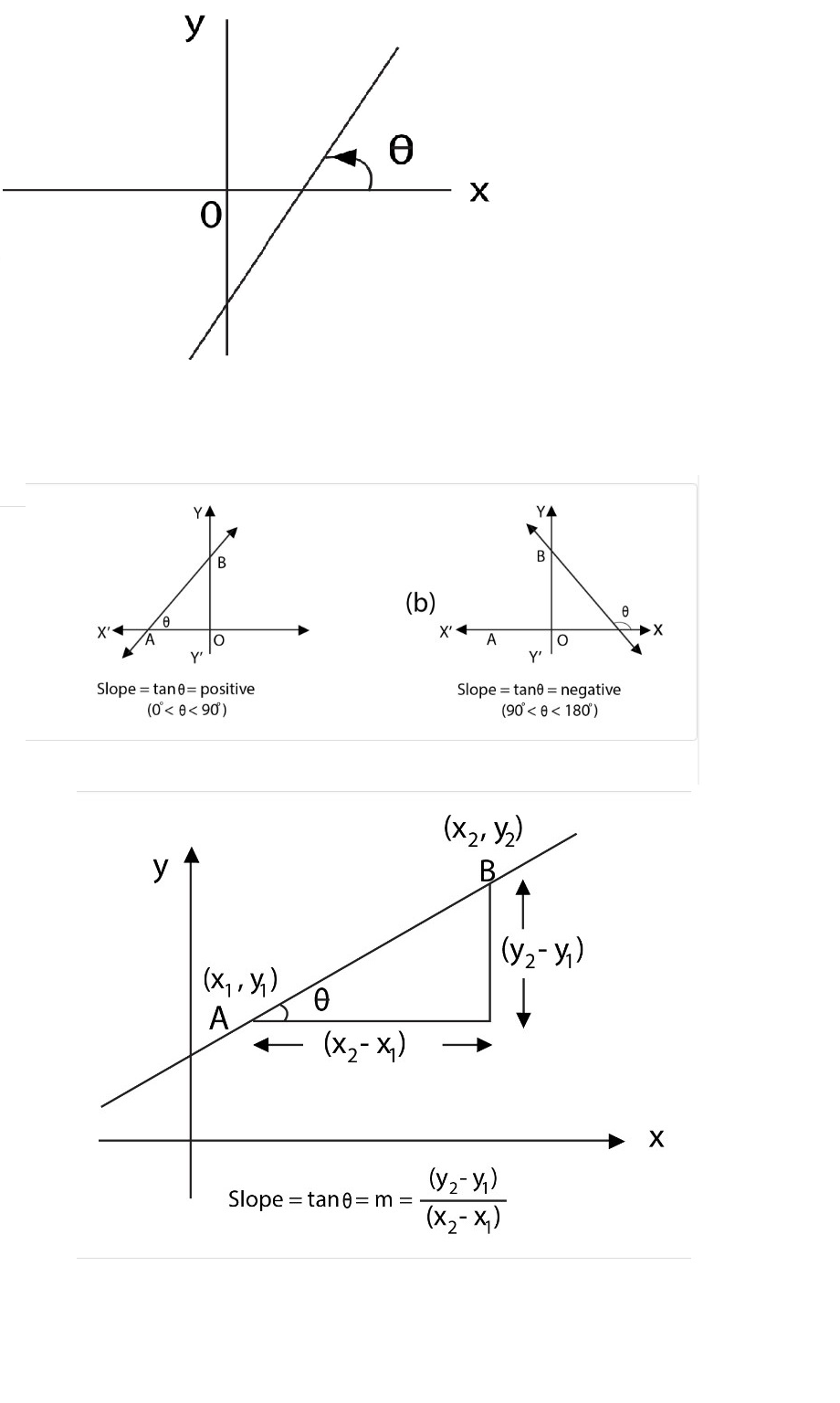
lf a straight line intersects the `x`-axis, the inclination of the line is defined as the measure of the smallest non-negative angle which the line makes with the positive direction of the `x`-axis.
`text(Slope and Gradient of a line :)`
lf the inclination of a line (i.e. non vertical line) is `theta` and `theta ne pi/2` , then the slope of a line is defined to be `tan theta` and is denoted by `m`.
`theta` is positive or negative according as it `theta` is measured in anticlockwise or clockwise
direction.
`Fundas :`
i) When two lines are parallel, they have the same inclination.
ii) `0 le theta < 180^(circ)` `(theta ne 90^(circ))`
iii) If `theta=0` then line is parallel to `x`-axis
lf `theta = 90^(circ)` then line is perpendicular to `x`-axis or parallel to `y`-axis.
iv) lf `A(x_1,y_1)` & `B (x_2, y_2), x_1 ne x_2` are points on a straight line then the slope `m` of the line is given by
`tantheta = m=((y_2-y_1))/((x_2-x_1))` (From fig.)
v) If the intercepts made by the line are of opposite sign then slope is positive.
vi) If the intercepts made by the line are of same sign then slope is negative.
lf a straight line intersects the `x`-axis, the inclination of the line is defined as the measure of the smallest non-negative angle which the line makes with the positive direction of the `x`-axis.
`text(Slope and Gradient of a line :)`
lf the inclination of a line (i.e. non vertical line) is `theta` and `theta ne pi/2` , then the slope of a line is defined to be `tan theta` and is denoted by `m`.
`theta` is positive or negative according as it `theta` is measured in anticlockwise or clockwise
direction.
`Fundas :`
i) When two lines are parallel, they have the same inclination.
ii) `0 le theta < 180^(circ)` `(theta ne 90^(circ))`
iii) If `theta=0` then line is parallel to `x`-axis
lf `theta = 90^(circ)` then line is perpendicular to `x`-axis or parallel to `y`-axis.
iv) lf `A(x_1,y_1)` & `B (x_2, y_2), x_1 ne x_2` are points on a straight line then the slope `m` of the line is given by
`tantheta = m=((y_2-y_1))/((x_2-x_1))` (From fig.)
v) If the intercepts made by the line are of opposite sign then slope is positive.
vi) If the intercepts made by the line are of same sign then slope is negative.