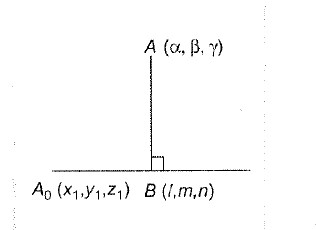
(i) If `a` vector `vecr = a hat i + b hat j + c hat k` having direction cosines `l, m` and `n`,then
`l= a/(|r|) , m=b/(|r|)` and `n= c/(|r|)`
where, `a, b` and `c` are direction ratios of `r`.
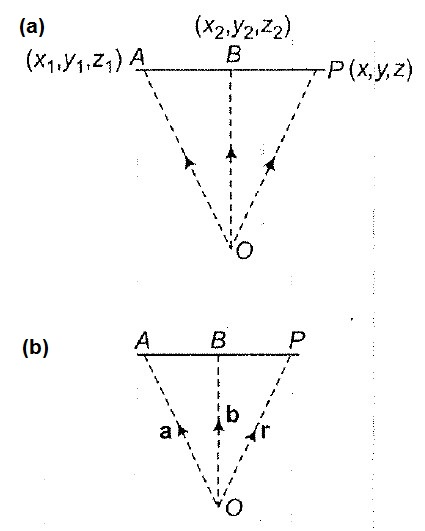
(ii) Direction ratios of the line joining two points `P(x_1,y_1,z_1) ` and `Q(x_2 ,y_2 ,z_2 )` are `x_2 -x_1,y_2 -y_1,
z_2 - z_1` and its direction cosines are
`(x_2-x_1)/(|PQ|) , (y_2-y_1)/(|PQ|) , (z_2-z_1)/(|PQ|)`
(iii) lf `P (x, y,z)` is a point in space, then
(a) `x = l| r |, y = m | r|, z = n | r|`
(b) `l| r |, m | r |` and `n | r |` are projections of `r` on
`OX, OY` and `OZ`, respectively.
(c) `vec r = | r | (l hat i + m hat j + n hat k)`
(iv) The projection of the line segment joining points `P(x_1 , y_1, z_1)` and `Q(x_2 , y_2 , z_2)` to the line having
direction cosines `l,m, n,` is
`|(x_2 - x_1 )l + (y_2 - y_1 )m + (z_2 - z_1 )n|`.
(v) The sum of squares of direction cosines is always unity i.e. `l^2 + m^2 + n^2=1`
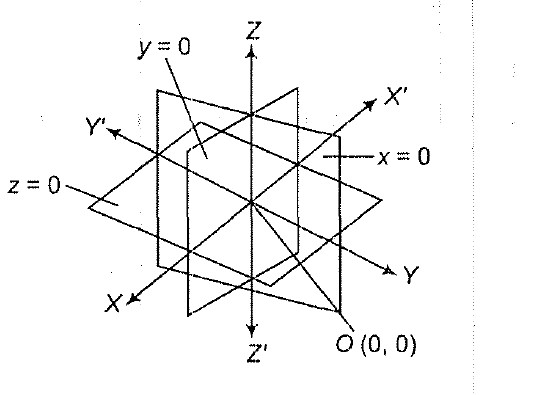
(vi) DC's of `X, Y` and `Z`-axes are `(1, 0, 0), (0, 1, 0)` and `(0, 0, 1)`.
(vii) Direction cosines of a line are unique but direction ratio of a line are not unique and can be infinite.
(viii) DC's of a line which is equally inclined to the coordinate axes, are `(pm 1/(sqrt 3) , pm 1/(sqrt 3) , pm 1/(sqrt 3))`
(i) If `a` vector `vecr = a hat i + b hat j + c hat k` having direction cosines `l, m` and `n`,then
`l= a/(|r|) , m=b/(|r|)` and `n= c/(|r|)`
where, `a, b` and `c` are direction ratios of `r`.
(ii) Direction ratios of the line joining two points `P(x_1,y_1,z_1) ` and `Q(x_2 ,y_2 ,z_2 )` are `x_2 -x_1,y_2 -y_1,
z_2 - z_1` and its direction cosines are
`(x_2-x_1)/(|PQ|) , (y_2-y_1)/(|PQ|) , (z_2-z_1)/(|PQ|)`
(iii) lf `P (x, y,z)` is a point in space, then
(a) `x = l| r |, y = m | r|, z = n | r|`
(b) `l| r |, m | r |` and `n | r |` are projections of `r` on
`OX, OY` and `OZ`, respectively.
(c) `vec r = | r | (l hat i + m hat j + n hat k)`
(iv) The projection of the line segment joining points `P(x_1 , y_1, z_1)` and `Q(x_2 , y_2 , z_2)` to the line having
direction cosines `l,m, n,` is
`|(x_2 - x_1 )l + (y_2 - y_1 )m + (z_2 - z_1 )n|`.
(v) The sum of squares of direction cosines is always unity i.e. `l^2 + m^2 + n^2=1`
(vi) DC's of `X, Y` and `Z`-axes are `(1, 0, 0), (0, 1, 0)` and `(0, 0, 1)`.
(vii) Direction cosines of a line are unique but direction ratio of a line are not unique and can be infinite.
(viii) DC's of a line which is equally inclined to the coordinate axes, are `(pm 1/(sqrt 3) , pm 1/(sqrt 3) , pm 1/(sqrt 3))`