(1)
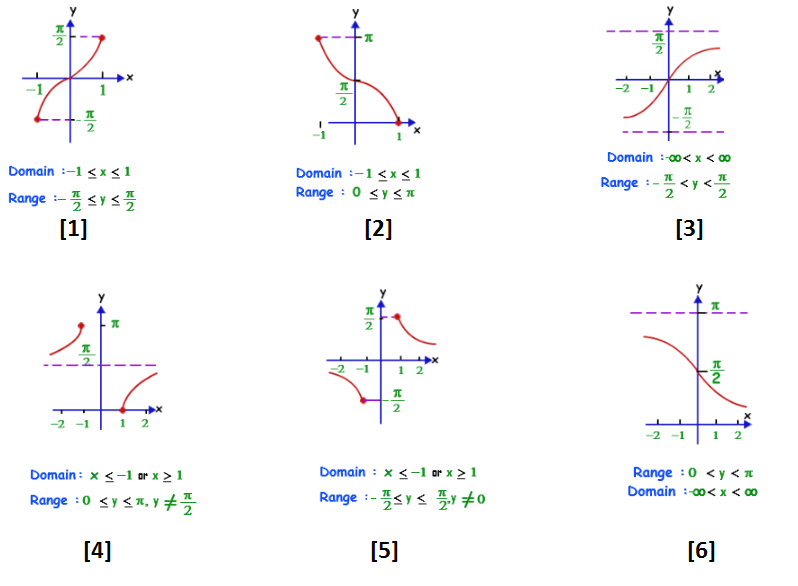
`sin (sin^-1 x) = x, x ∈ [– 1, 1]` and `sin^-1 (sin x) = x, x ∈ [ - pi/2, pi/2]`
`cos (cos^-1 x) = x, x ∈ [– 1, 1]` and `cos ^-1 (cos x) = x, x ∈ [ 0,pi]`
`tan (tan^-1 x) = x, x ∈ R` and `tan^-1 (tan x) = x, x ∈ ( - pi/2, pi/2)`
`cosec (cosec^-1 x) = x, |x| ge 1` and `cosec^-1 (cosec x) = x, x ∈ [ - pi/2, pi/2] , xne0`
`sec (sec^-1 x) = x, |x| ge 1` and `sec^-1 (sec x) = x, x ∈ [ 0, pi], x ne pi/2`
`cot (cot^-1 x) = x, x ∈ R` and `cot^-1 (cot x) = x, x ∈ ( 0,pi)`
(2)
• `sin ^-1 \ \1/x = cosec^-1 x , x >= 1 ` or ` x <= -1`
• `cos^-1 \ \ 1/x = sec^-1 x, x ≥ 1` or `x ≤ – 1`
• `tan ^-1 \ \ 1/x = cot^-1 x , x > 0`
To prove the first result, we put `cosec^-1 x = y`, i.e., x = cosec y
Therefore `1/x = sin y`
Hence `sin^-1 \ \1/x = y`
or ` sin ^-1 \ \1/x = cosec^-1 x`
Similarly, we can prove the other parts.
(3)
(i) `sin^-1 (–x) = – sin^-1 x, x ∈ [– 1, 1]`
(ii) `tan^-1 (–x) = – tan^-1 x, x ∈ R`
(iii) `cosec^-1 (–x) = – cosec^-1 x, | x | ≥ 1`
Let `sin^-1 (–x) = y`, i.e., `–x = sin y` so that `x = – sin y`, i.e., `x = sin (–y)`.
Hence `sin^-1 x = – y = – sin^-1 (–x)`
Therefore `sin^-1 (–x) = – sin^-1 x`
Similarly, we can prove the other parts.
(i) `cos^-1 (–x) = π – cos^-1 x, x ∈ [– 1, 1]`
(ii) `sec^-1 (–x) = π – sec^-1 x, | x | ≥ 1`
(iii) `cot^-1 (–x) = π – cot^-1 x, x ∈ R`
Let `cos^-1 (–x) = y` i.e., `– x = cos y` so that `x = – cos y = cos (π – y)`
Therefore `cos^-1 x = π – y = π – cos^-1 (–x)`
Hence `cos^-1 (–x) = π – cos^-1 x`
Similarly, we can prove the other parts.
4)
(i) `sin^-1 x + cos^-1 x = pi/2, x ∈ [– 1, 1]`
(ii) `tan^-1 x + cot^-1 x = π/2, x ∈ R`
(iii) `cosec^-1 x + sec^-1 x = pi/2 , | x| >= 1`
Let `sin^-1 x = y`. Then `x = sin y = cos ( pi/2 - y)`
Therefore `cos^-1 x = pi/2 - y = pi/2 - sin ^-1 x`
Hence `sin^-1 x + cos^-1 x = pi/2`
Similarly, we can prove the other parts.
5)
(i) `tan^-1x + tan^-1 y = tan^-1 \ \( x +y)/( 1 - xy) , xy < 1`
(ii) `tan^-1x – tan^-1 y = tan^-1 \ \( x - y)/( 1 + xy), xy > -1`
(iii) `2tan^-1x = tan^-1\ \ (2x ) /( 1- x^2) , | x | < 1`
Let `tan^-1 x = θ` and `tan^-1 y = phi`. Then `x = tan θ, y = tan phi`
Now `tan ( theta + pi) = ( tan theta + tan phi )/( 1- tan theta tan phi ) = ( x + y) /( 1- xy)`
This gives ` theta + phi = tan ^-1 \ \ ( x+y) /(1 -xy)`
Hence ` tan ^-1 a + tan ^-1 y = tan^-1 \ \ ( x +y) /(1 -xy)`
In the above result, if we replace y by – y, we get the second result and by replacing y by x, we get the third result.
6)
(i) `2tan^-1 x = sin^-1 \ \( 2x) /( 1 + x^2) , | x| <=1`
(ii) `2tan^-1 x = cos^-1 \ \( 1- x^2 ) /( 1 +x^2 ) , x >= 0`
(iii) `2 tan^-1 x = tan^-1 \ \ (2 x) /(1 -x^2 ) . -1 < x < 1`
Let `tan^-1 x = y`, then `x = tan y`. Now
`sin^-1 \ \ ( 2 x) /( 1 + x^2) = sin^-1 \ \ ( 2 tan y) /( 1 + tan^2 y)`
`= sin^-1 (sin 2y) = 2y = 2tan^-1 x`
Also `cos^-1 \ \ ( 1 - x^2 ) /( 1 +x^2) = cos^-1 \ \ ( 1 - tan^2y)/( 1 + tan^2y) = cos ^-1 \ \ ( cos 2y ) = 2y = 2 tan ^-1 x`
7)
`sin^(-1)x + sin^(-1)y = sin^(-1)(xsqrt(1-y^2) + y sqrt(1-x^2))`
`sin^(-1)x - sin^(-1)y = sin^(-1)(xsqrt(1-y^2) - y sqrt(1-x^2))`
`cos^(-1)x + cos^(-1)y = cos^(-1)(xy - sqrt(1-x^2) .sqrt(1-x^2))`
`cos^(-1)x + cos^(-1)y = cos^(-1)(xy + sqrt(1-x^2) .sqrt(1-x^2))`
(1)
`sin (sin^-1 x) = x, x ∈ [– 1, 1]` and `sin^-1 (sin x) = x, x ∈ [ - pi/2, pi/2]`
`cos (cos^-1 x) = x, x ∈ [– 1, 1]` and `cos ^-1 (cos x) = x, x ∈ [ 0,pi]`
`tan (tan^-1 x) = x, x ∈ R` and `tan^-1 (tan x) = x, x ∈ ( - pi/2, pi/2)`
`cosec (cosec^-1 x) = x, |x| ge 1` and `cosec^-1 (cosec x) = x, x ∈ [ - pi/2, pi/2] , xne0`
`sec (sec^-1 x) = x, |x| ge 1` and `sec^-1 (sec x) = x, x ∈ [ 0, pi], x ne pi/2`
`cot (cot^-1 x) = x, x ∈ R` and `cot^-1 (cot x) = x, x ∈ ( 0,pi)`
(2)
• `sin ^-1 \ \1/x = cosec^-1 x , x >= 1 ` or ` x <= -1`
• `cos^-1 \ \ 1/x = sec^-1 x, x ≥ 1` or `x ≤ – 1`
• `tan ^-1 \ \ 1/x = cot^-1 x , x > 0`
To prove the first result, we put `cosec^-1 x = y`, i.e., x = cosec y
Therefore `1/x = sin y`
Hence `sin^-1 \ \1/x = y`
or ` sin ^-1 \ \1/x = cosec^-1 x`
Similarly, we can prove the other parts.
(3)
(i) `sin^-1 (–x) = – sin^-1 x, x ∈ [– 1, 1]`
(ii) `tan^-1 (–x) = – tan^-1 x, x ∈ R`
(iii) `cosec^-1 (–x) = – cosec^-1 x, | x | ≥ 1`
Let `sin^-1 (–x) = y`, i.e., `–x = sin y` so that `x = – sin y`, i.e., `x = sin (–y)`.
Hence `sin^-1 x = – y = – sin^-1 (–x)`
Therefore `sin^-1 (–x) = – sin^-1 x`
Similarly, we can prove the other parts.
(i) `cos^-1 (–x) = π – cos^-1 x, x ∈ [– 1, 1]`
(ii) `sec^-1 (–x) = π – sec^-1 x, | x | ≥ 1`
(iii) `cot^-1 (–x) = π – cot^-1 x, x ∈ R`
Let `cos^-1 (–x) = y` i.e., `– x = cos y` so that `x = – cos y = cos (π – y)`
Therefore `cos^-1 x = π – y = π – cos^-1 (–x)`
Hence `cos^-1 (–x) = π – cos^-1 x`
Similarly, we can prove the other parts.
4)
(i) `sin^-1 x + cos^-1 x = pi/2, x ∈ [– 1, 1]`
(ii) `tan^-1 x + cot^-1 x = π/2, x ∈ R`
(iii) `cosec^-1 x + sec^-1 x = pi/2 , | x| >= 1`
Let `sin^-1 x = y`. Then `x = sin y = cos ( pi/2 - y)`
Therefore `cos^-1 x = pi/2 - y = pi/2 - sin ^-1 x`
Hence `sin^-1 x + cos^-1 x = pi/2`
Similarly, we can prove the other parts.
5)
(i) `tan^-1x + tan^-1 y = tan^-1 \ \( x +y)/( 1 - xy) , xy < 1`
(ii) `tan^-1x – tan^-1 y = tan^-1 \ \( x - y)/( 1 + xy), xy > -1`
(iii) `2tan^-1x = tan^-1\ \ (2x ) /( 1- x^2) , | x | < 1`
Let `tan^-1 x = θ` and `tan^-1 y = phi`. Then `x = tan θ, y = tan phi`
Now `tan ( theta + pi) = ( tan theta + tan phi )/( 1- tan theta tan phi ) = ( x + y) /( 1- xy)`
This gives ` theta + phi = tan ^-1 \ \ ( x+y) /(1 -xy)`
Hence ` tan ^-1 a + tan ^-1 y = tan^-1 \ \ ( x +y) /(1 -xy)`
In the above result, if we replace y by – y, we get the second result and by replacing y by x, we get the third result.
6)
(i) `2tan^-1 x = sin^-1 \ \( 2x) /( 1 + x^2) , | x| <=1`
(ii) `2tan^-1 x = cos^-1 \ \( 1- x^2 ) /( 1 +x^2 ) , x >= 0`
(iii) `2 tan^-1 x = tan^-1 \ \ (2 x) /(1 -x^2 ) . -1 < x < 1`
Let `tan^-1 x = y`, then `x = tan y`. Now
`sin^-1 \ \ ( 2 x) /( 1 + x^2) = sin^-1 \ \ ( 2 tan y) /( 1 + tan^2 y)`
`= sin^-1 (sin 2y) = 2y = 2tan^-1 x`
Also `cos^-1 \ \ ( 1 - x^2 ) /( 1 +x^2) = cos^-1 \ \ ( 1 - tan^2y)/( 1 + tan^2y) = cos ^-1 \ \ ( cos 2y ) = 2y = 2 tan ^-1 x`
7)
`sin^(-1)x + sin^(-1)y = sin^(-1)(xsqrt(1-y^2) + y sqrt(1-x^2))`
`sin^(-1)x - sin^(-1)y = sin^(-1)(xsqrt(1-y^2) - y sqrt(1-x^2))`
`cos^(-1)x + cos^(-1)y = cos^(-1)(xy - sqrt(1-x^2) .sqrt(1-x^2))`
`cos^(-1)x + cos^(-1)y = cos^(-1)(xy + sqrt(1-x^2) .sqrt(1-x^2))`