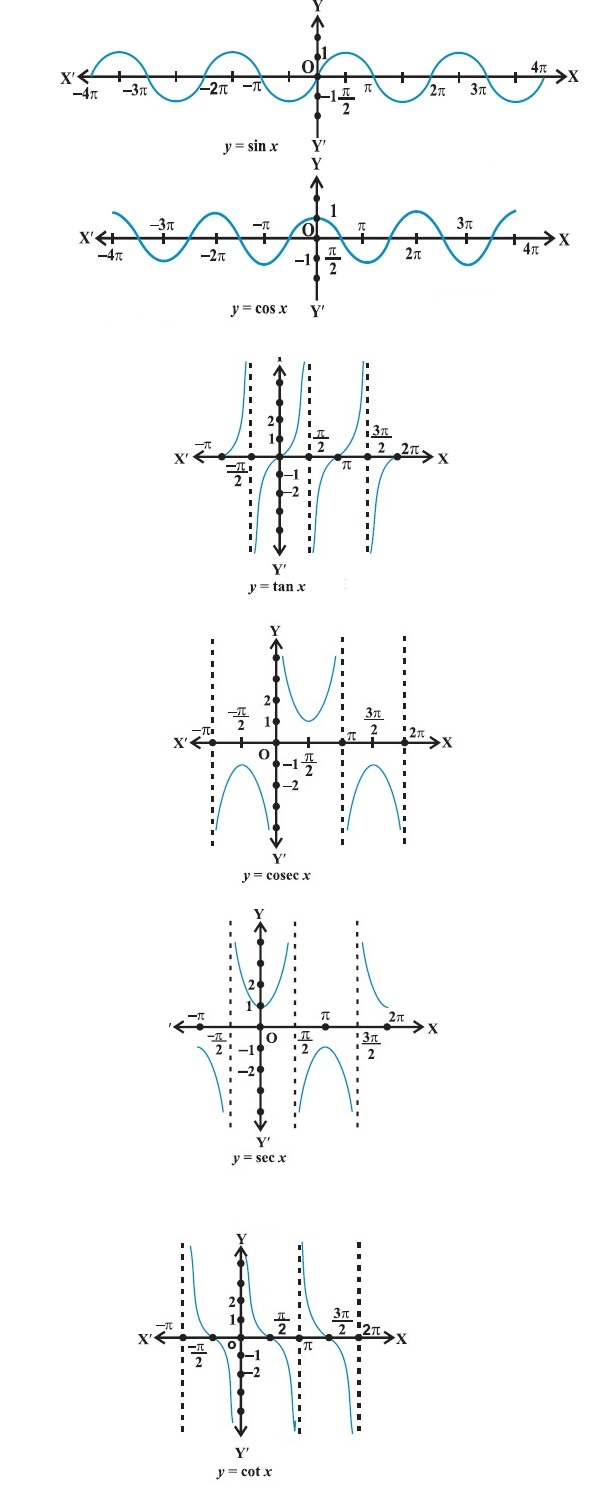
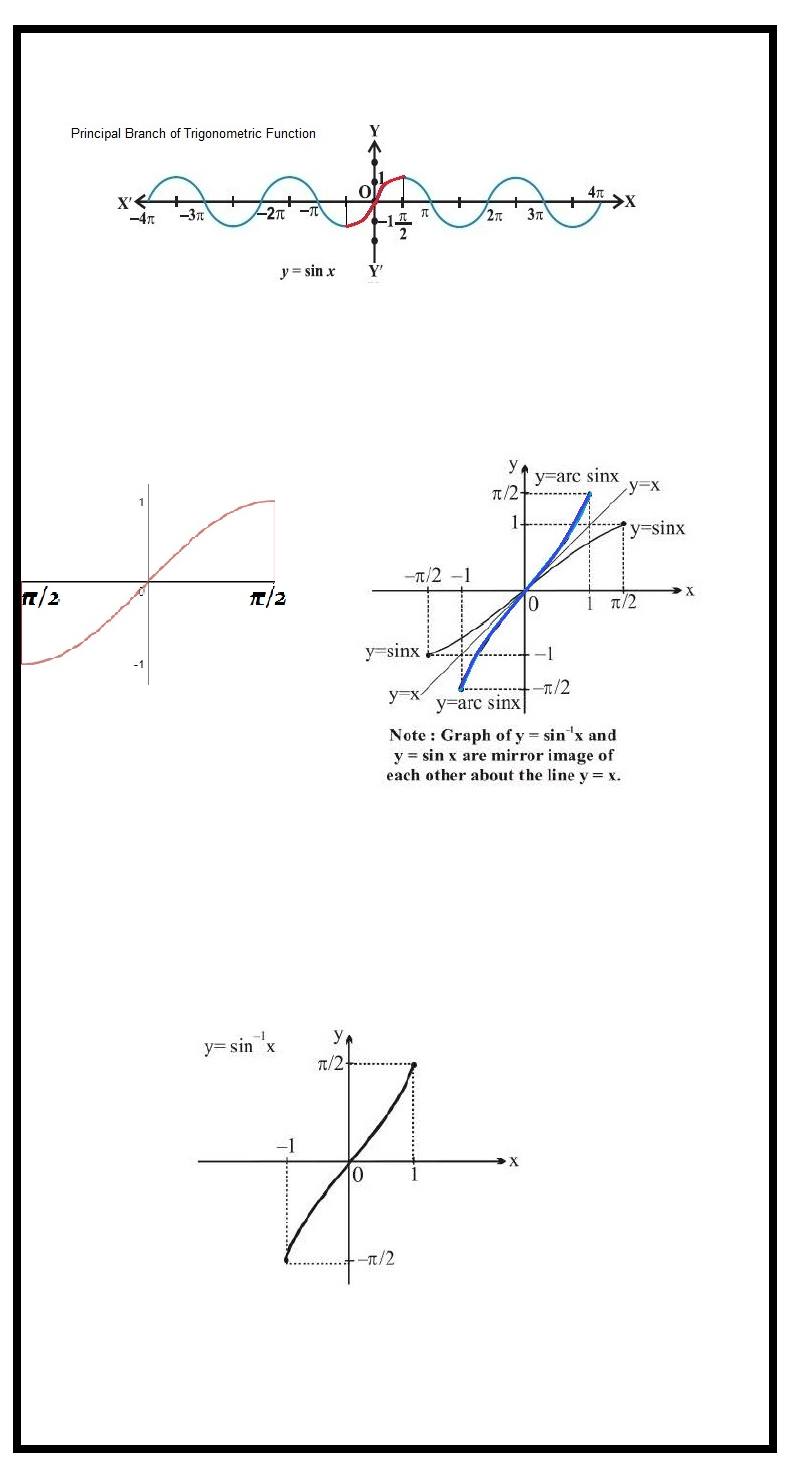
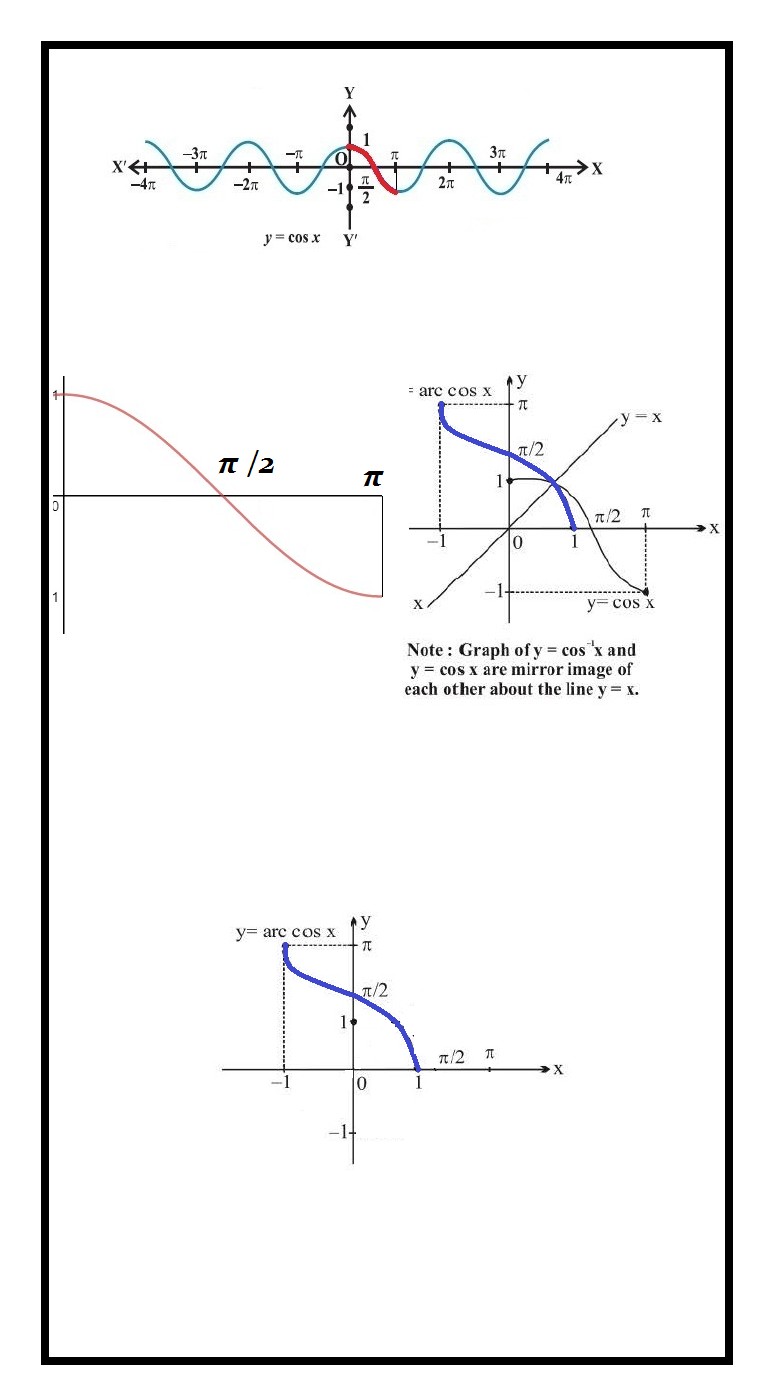
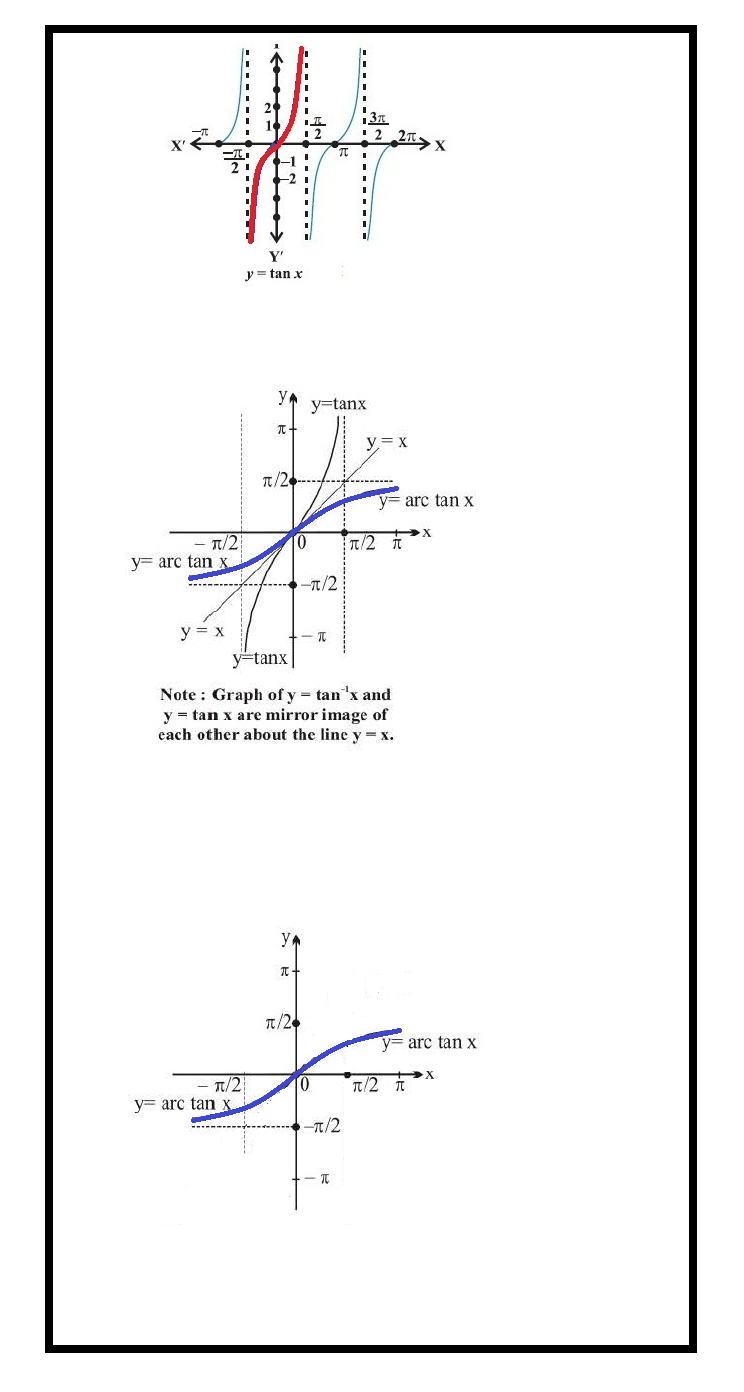
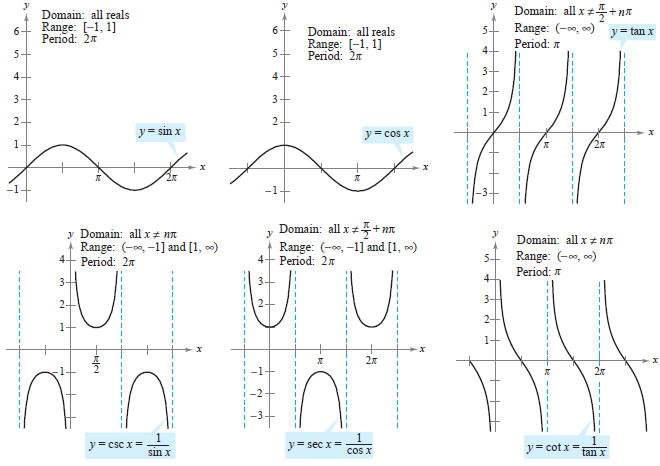
we have studied trigonometric functions, which are defined as follows:
1. sine function, i.e.,
`sin : R → [– 1, 1]`
2. cosine function, i.e.,
` cos : R → [– 1, 1]`
3. tangent function, i.e., `tan : R – { x : x = (2n + 1) π/2 , n ∈ Z} → R`
4. cotangent function, i.e.,
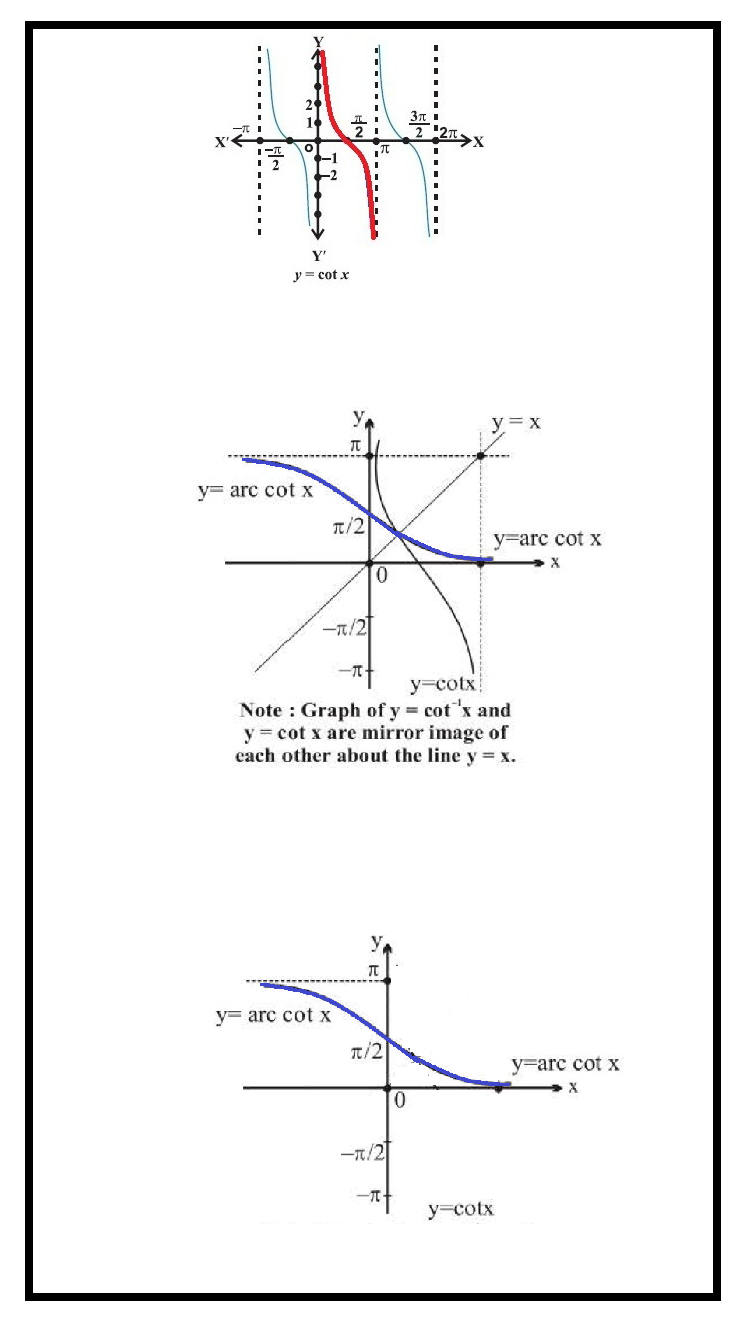
`cot : R – { x : x = nπ, n ∈ Z} → R`
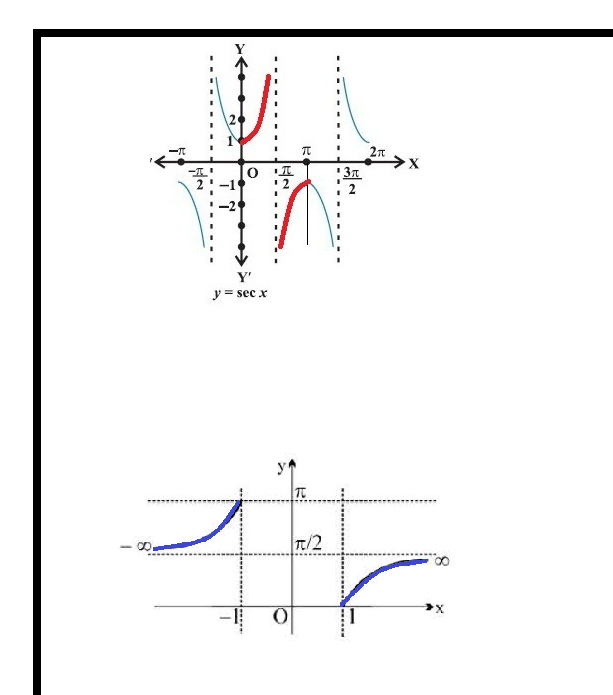
5.secant function, i.e., `sec : R – { x : x = (2n + 1)π/2 , n ∈ Z} → R – (– 1, 1)`
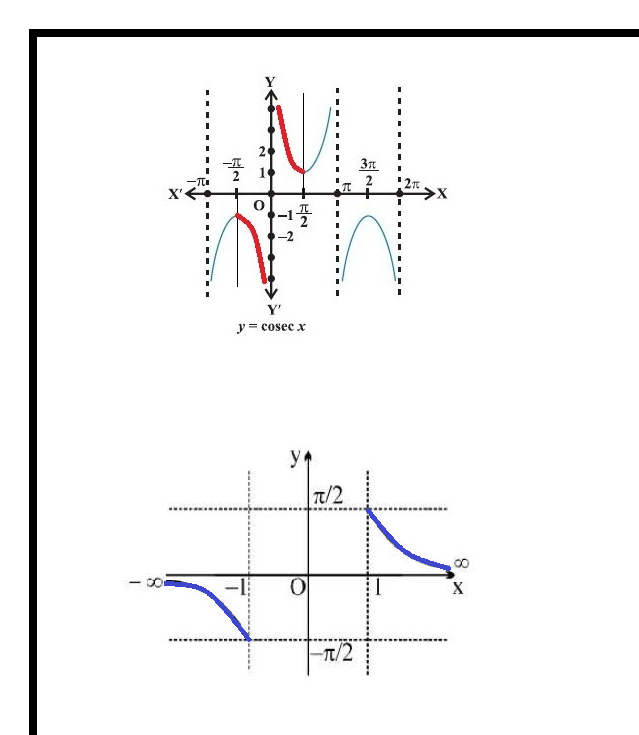
6. cosecant function, i.e., `cosec : R – { x : x = nπ, n ∈ Z} → R – (– 1, 1)`
.jpg)
we have studied trigonometric functions, which are defined as follows:
1. sine function, i.e.,
`sin : R → [– 1, 1]`
2. cosine function, i.e.,
` cos : R → [– 1, 1]`
3. tangent function, i.e., `tan : R – { x : x = (2n + 1) π/2 , n ∈ Z} → R`
4. cotangent function, i.e.,
`cot : R – { x : x = nπ, n ∈ Z} → R`
5.secant function, i.e., `sec : R – { x : x = (2n + 1)π/2 , n ∈ Z} → R – (– 1, 1)`
6. cosecant function, i.e., `cosec : R – { x : x = nπ, n ∈ Z} → R – (– 1, 1)`

.jpg)


.jpg)