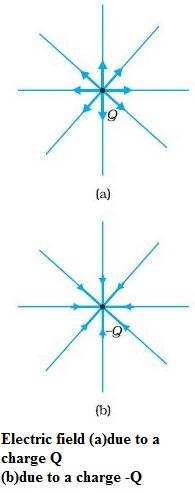
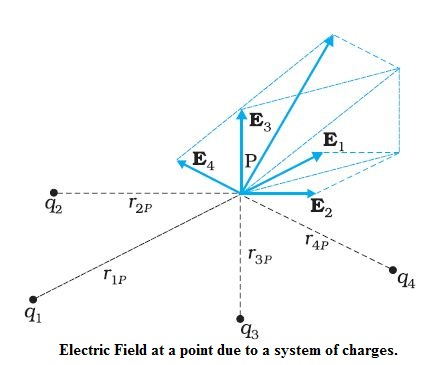
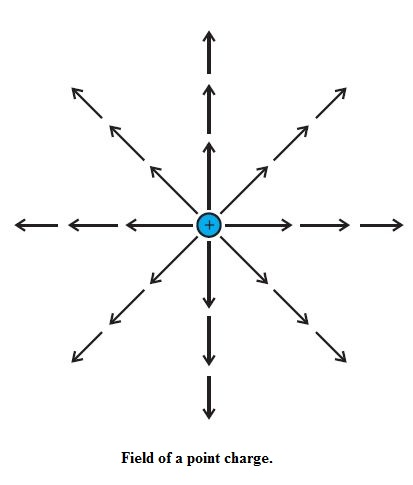
FORCES BETWEEN MULTIPLE CHARGES

`color {blue}✍️ ` Consider a system of three charges ` q_1`, `q_2` and `q_3`.
The force on charge` q_1`, due to two other charges `q_2`, `q_3` can be obtained by performing a vector addition of the forces due to each one of these charges. Thus, if the force on `q_1` due to `q_2` is denoted by `vec F_(12)`,
`vec F_(12)=1/(4πε_0)((q_1q_2)/r_(12)^2)hat r_(12)`
The force on `q_1` due to `q_3`, denoted by `vec F_13`, is given by
`vec F_(13)=1/(4πε_0)((q_1q_3)/r_(13)^2)hat r_(13)`
which is the Coulomb force on `q_1` due to `q_3`
Thus the total force`vec F_1` on `q_1` due to the two charges `q_2` and `q_3` is given as :
`vec F_1 = vec F_(12) +vec F_(13) =1/(4πε_0)((q_1q_2)/r_(12)^2)hat r_(12)+1/(4πε_0)((q_1q_3)/r_(13)^2)hat r_(13)`
The principle of superposition says that in a system of charges `q_1, q_2, ..., q_n`, the force on `q_1` due to `q_2` is the same as given by Coulomb’s law, i.e., it is unaffected by the presence of the other charges `q_3, q_4, ..., q_n`.
The total force `vec F_1` on the charge `q_1`, due to all other charges, is then given by the vector sum of the forces `vec F_(12), vec F_(13), ...,vec F_(1n)`:
`\color{red}ul(★ \color{red} " FORMULA ALERT")`
`vec F_1 = vec F_(12) +vec F_(13) + ...... +vec F_(1n)`
` =1/(4πε_0)[(q_1q_2)/r_(12)^2hat r_(12)+(q_1q_3)/r_(13)^2hat r_(13) +............ +(q_1q_n)/r_(1n)^2hat r_(1n)]`
`=q_1/(4πε_0)sum_(i=2)^(n)q_i/r_(1i)^2hat r_(1i)`
The vector sum is obtained by the parallelogram law of addition of vectors.
The force on charge` q_1`, due to two other charges `q_2`, `q_3` can be obtained by performing a vector addition of the forces due to each one of these charges. Thus, if the force on `q_1` due to `q_2` is denoted by `vec F_(12)`,
`vec F_(12)=1/(4πε_0)((q_1q_2)/r_(12)^2)hat r_(12)`
The force on `q_1` due to `q_3`, denoted by `vec F_13`, is given by
`vec F_(13)=1/(4πε_0)((q_1q_3)/r_(13)^2)hat r_(13)`
which is the Coulomb force on `q_1` due to `q_3`
Thus the total force`vec F_1` on `q_1` due to the two charges `q_2` and `q_3` is given as :
`vec F_1 = vec F_(12) +vec F_(13) =1/(4πε_0)((q_1q_2)/r_(12)^2)hat r_(12)+1/(4πε_0)((q_1q_3)/r_(13)^2)hat r_(13)`
The principle of superposition says that in a system of charges `q_1, q_2, ..., q_n`, the force on `q_1` due to `q_2` is the same as given by Coulomb’s law, i.e., it is unaffected by the presence of the other charges `q_3, q_4, ..., q_n`.
The total force `vec F_1` on the charge `q_1`, due to all other charges, is then given by the vector sum of the forces `vec F_(12), vec F_(13), ...,vec F_(1n)`:
`\color{red}ul(★ \color{red} " FORMULA ALERT")`
`vec F_1 = vec F_(12) +vec F_(13) + ...... +vec F_(1n)`
` =1/(4πε_0)[(q_1q_2)/r_(12)^2hat r_(12)+(q_1q_3)/r_(13)^2hat r_(13) +............ +(q_1q_n)/r_(1n)^2hat r_(1n)]`
`=q_1/(4πε_0)sum_(i=2)^(n)q_i/r_(1i)^2hat r_(1i)`
The vector sum is obtained by the parallelogram law of addition of vectors.