`=>` The vector product of two nonzero vectors `vec a` and `vec b` , is denoted by `vec a xx vec b`
and defined as
`color{green}{vec a xx vec b = | vec a | | vec b | sin theta hat n ,}`
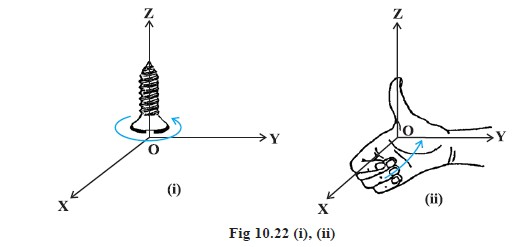
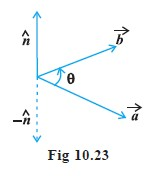
`=>`where, `θ` is the angle between `vec a` and `vec b` , ` 0 ≤ θ ≤ π ` and `hat n` is a unit vector perpendicular to both `vec a ` and `vec b` , such that `vec a , vec b` and `hat n` form a right handed system (Fig).
i.e., the right handed system rotated from `vec a` to ` vec b` moves in the direction of `hat n` .
● If either `vec a = vec 0` or `vec b = vec 0` , then θ is not defined and in this case, we define `vec a xx vec b = vec 0`
`"Point to consider :"`
1. `vec a xx vec b` is a vector.
2. Let `vec a` and `vec b` be two nonzero vectors. Then `vec a xx vec b = vec 0` if and only if `vec a` and `vec b`
are parallel (or collinear) to each other, i.e., `color{red}{vec a xx vec b = vec 0 ⇔ vec a ∥ vec b}`
`=>` In particular, `vec a xx vec a = vec 0` and `vec a xx ( - vec a ) = vec 0` , since in the first situation, θ = 0
and in the second one, θ = π, making the value of sin θ to be 0.
3 . If ` θ = π/2` then `vec a xx vec b= | vec a | | vec b |` .
4. In view of the Observations 2 and 3, for mutually perpendicular
unit vectors `hat i , hat j` and `hat k` (Fig 10.24), we have
`hat i xx hat i = hat j xx hat j = hat k xx hat k = vec 0`
`hat i xx hat j = hat k , hat j xx hat k = hat i , hat k xx hat i = hat j`

5. In terms of vector product, the angle between two vectors `vec a` and `vec b` may be
given as
`color{red}{sin θ = ( | vec a xx vec b | )/( | vec a | | vec b | )}`
6. It is always true that the vector product is not commutative, as `vec a xx vec b = - vec b xx vec a` Indeed, `vec a xx vec b = | vec a | | vec b| sin θ hat n` , where `vec a , vec b` and `hat n` form a right handed system,
i.e., ` θ ` is traversed from `vec a` to `vec b` Fig 10.25 (i). While `vec b xx vec a = | vec a | | vec b| sin θ hat (n_1) ` , where
`vec b , vec a` and `hat (n_1) ` form a right handed system i.e. θ is traversed from `vec b` to `vec a ` ,
Fig(ii).

`=>` Thus, if we assume `vec a ` and `vec b` to lie in the plane of the paper, then `hat n` and `hat (n_1)` both will be perpendicular to the plane of the paper. But, `hat n` being directed above the
paper while `hat ( n_1) ` directed below the paper. i.e. `hat (n_1) = - hat n` .
Hence `vec a xx vec b = | vec a | | vec b | sin θ hat n`
`= - | vec a | | vec b| sin θ hat (n_1) = - vec b xx vec a`
7. In view of the Observations 4 and 6, we have
`hat j xx hat i = - hat k , hat k xx hat j = - hat i` and `hat i xx hat k = - hat j` .
8. If `vec a` and `vec b` represent the adjacent sides of a triangle then its area is given as
`= 1/2 | vec a xx vec b|` .
By definition of the area of a triangle, we have from Fig,

`=>` Area of triangle` ABC =1/2 AB * CD`
`=>` But `AB = | vec b | ` (as given), and `CD = | vec a | sin θ`.
`=>` Thus, Area of triangle` ABC =1/2 | vec b | | vec a | sin θ = 1/2 | vec a xx vec b |` .
9. If `vec a` and `vec b` represent the adjacent sides of a parallelogram, then its area is
given by ` | vec a xx vec b | ` .
From Fig, we have
Area of parallelogram `ABCD = AB * DE.`

But `AB = | vec b |` and `DE = | vec a | sin θ` .
Area of parallelogram `color{orange}{ABCD = | vec b | | vec a | sin θ = | vec a xx vec b |}` .
`=>` The vector product of two nonzero vectors `vec a` and `vec b` , is denoted by `vec a xx vec b`
and defined as
`color{green}{vec a xx vec b = | vec a | | vec b | sin theta hat n ,}`
`=>`where, `θ` is the angle between `vec a` and `vec b` , ` 0 ≤ θ ≤ π ` and `hat n` is a unit vector perpendicular to both `vec a ` and `vec b` , such that `vec a , vec b` and `hat n` form a right handed system (Fig).
i.e., the right handed system rotated from `vec a` to ` vec b` moves in the direction of `hat n` .
● If either `vec a = vec 0` or `vec b = vec 0` , then θ is not defined and in this case, we define `vec a xx vec b = vec 0`
`"Point to consider :"`
1. `vec a xx vec b` is a vector.
2. Let `vec a` and `vec b` be two nonzero vectors. Then `vec a xx vec b = vec 0` if and only if `vec a` and `vec b`
are parallel (or collinear) to each other, i.e., `color{red}{vec a xx vec b = vec 0 ⇔ vec a ∥ vec b}`
`=>` In particular, `vec a xx vec a = vec 0` and `vec a xx ( - vec a ) = vec 0` , since in the first situation, θ = 0
and in the second one, θ = π, making the value of sin θ to be 0.
3 . If ` θ = π/2` then `vec a xx vec b= | vec a | | vec b |` .
4. In view of the Observations 2 and 3, for mutually perpendicular
unit vectors `hat i , hat j` and `hat k` (Fig 10.24), we have
`hat i xx hat i = hat j xx hat j = hat k xx hat k = vec 0`
`hat i xx hat j = hat k , hat j xx hat k = hat i , hat k xx hat i = hat j`

5. In terms of vector product, the angle between two vectors `vec a` and `vec b` may be
given as
`color{red}{sin θ = ( | vec a xx vec b | )/( | vec a | | vec b | )}`
6. It is always true that the vector product is not commutative, as `vec a xx vec b = - vec b xx vec a` Indeed, `vec a xx vec b = | vec a | | vec b| sin θ hat n` , where `vec a , vec b` and `hat n` form a right handed system,
i.e., ` θ ` is traversed from `vec a` to `vec b` Fig 10.25 (i). While `vec b xx vec a = | vec a | | vec b| sin θ hat (n_1) ` , where
`vec b , vec a` and `hat (n_1) ` form a right handed system i.e. θ is traversed from `vec b` to `vec a ` ,
Fig(ii).

`=>` Thus, if we assume `vec a ` and `vec b` to lie in the plane of the paper, then `hat n` and `hat (n_1)` both will be perpendicular to the plane of the paper. But, `hat n` being directed above the
paper while `hat ( n_1) ` directed below the paper. i.e. `hat (n_1) = - hat n` .
Hence `vec a xx vec b = | vec a | | vec b | sin θ hat n`
`= - | vec a | | vec b| sin θ hat (n_1) = - vec b xx vec a`
7. In view of the Observations 4 and 6, we have
`hat j xx hat i = - hat k , hat k xx hat j = - hat i` and `hat i xx hat k = - hat j` .
8. If `vec a` and `vec b` represent the adjacent sides of a triangle then its area is given as
`= 1/2 | vec a xx vec b|` .
By definition of the area of a triangle, we have from Fig,

`=>` Area of triangle` ABC =1/2 AB * CD`
`=>` But `AB = | vec b | ` (as given), and `CD = | vec a | sin θ`.
`=>` Thus, Area of triangle` ABC =1/2 | vec b | | vec a | sin θ = 1/2 | vec a xx vec b |` .
9. If `vec a` and `vec b` represent the adjacent sides of a parallelogram, then its area is
given by ` | vec a xx vec b | ` .
From Fig, we have
Area of parallelogram `ABCD = AB * DE.`

But `AB = | vec b |` and `DE = | vec a | sin θ` .
Area of parallelogram `color{orange}{ABCD = | vec b | | vec a | sin θ = | vec a xx vec b |}` .