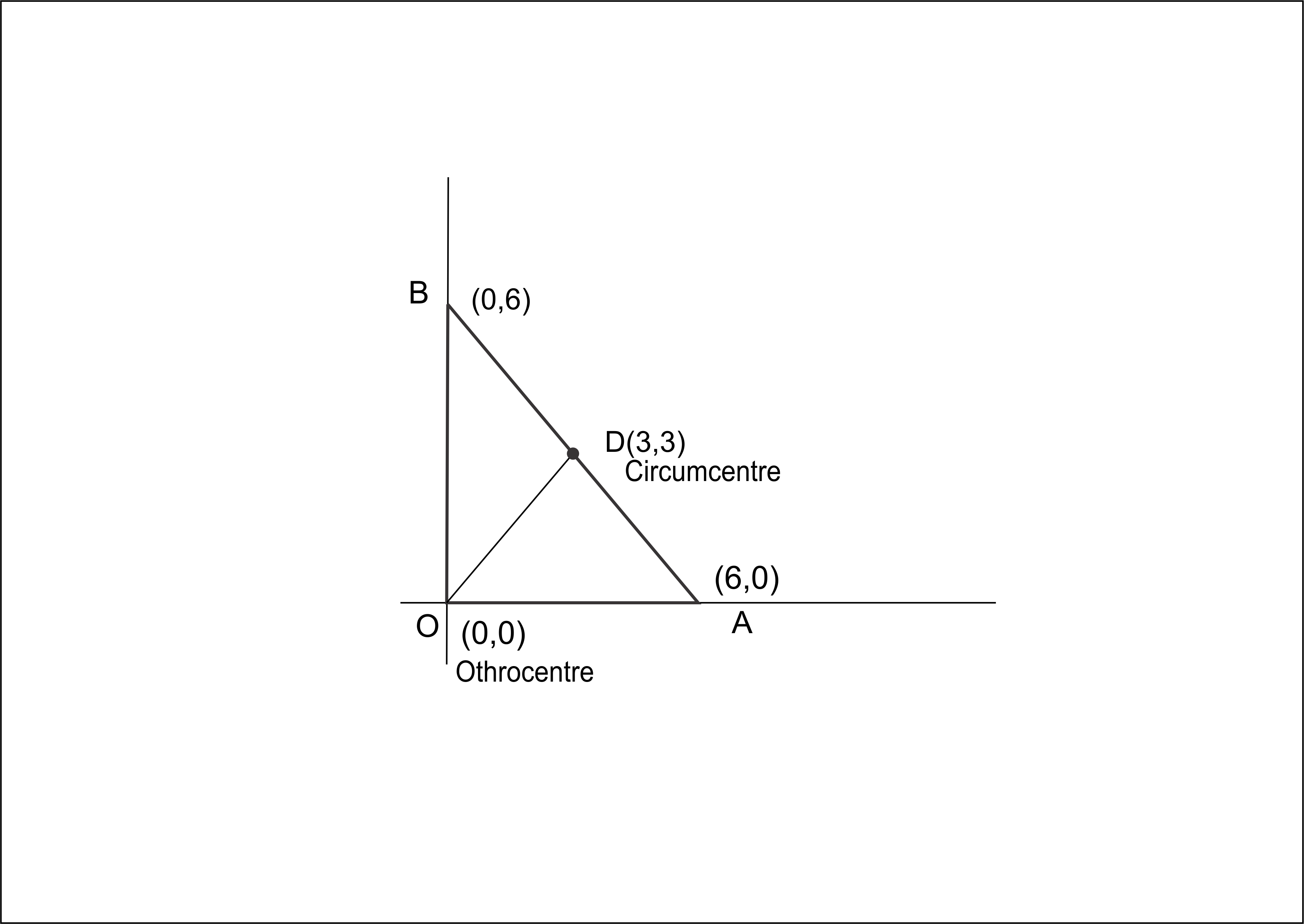Centroid (`G`) of Triangle

`Concept :`
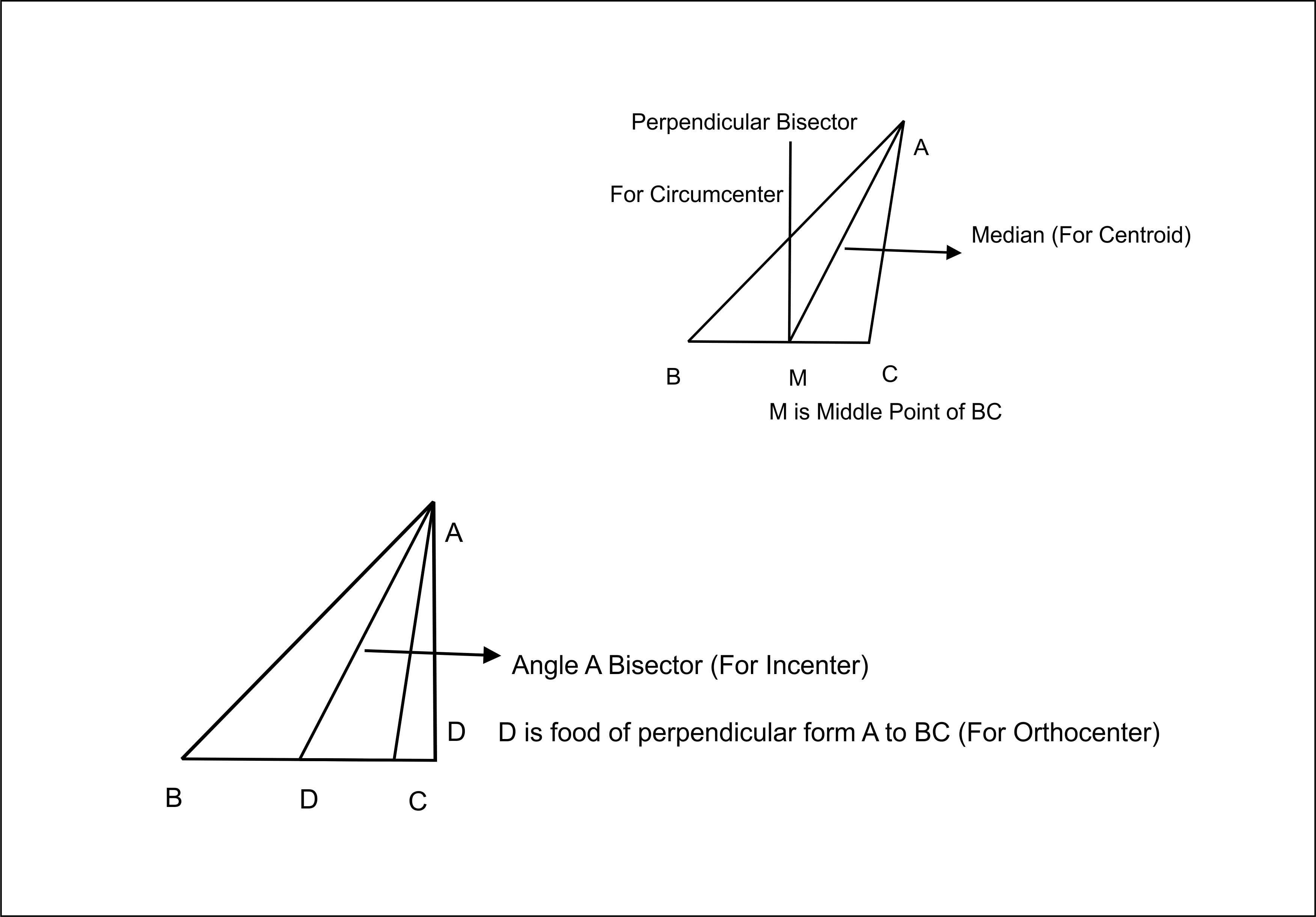
The point of intersection of the medians of a triangle is called the Centroid of the triangle.
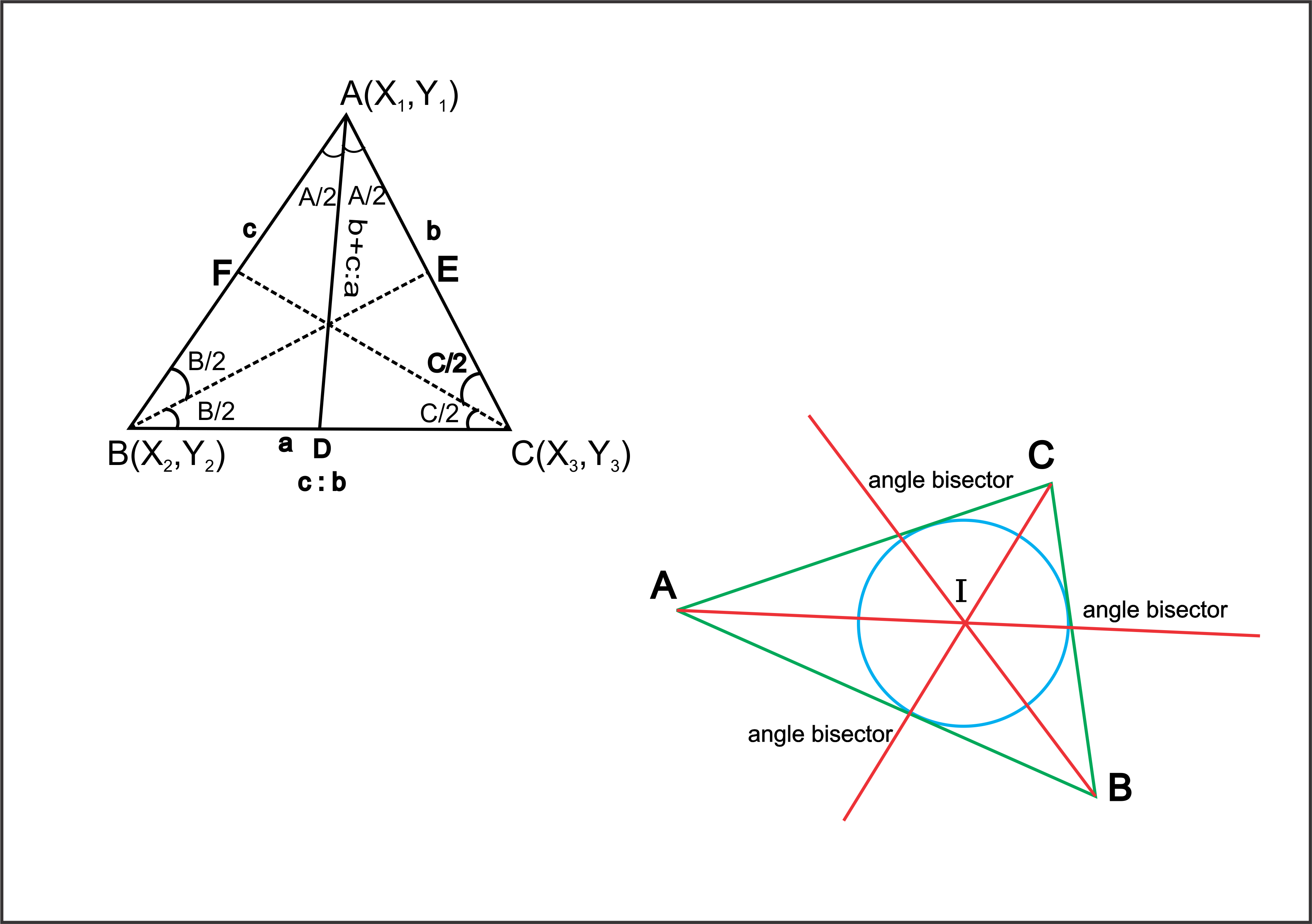
Median is the line joining `A` with middle point of `BC (D).` `( AD` , `BE` and `CF` are Medians in the image )
Medians are concurrent and point of intersection of Medians divides median in ratio of `2 : 1`
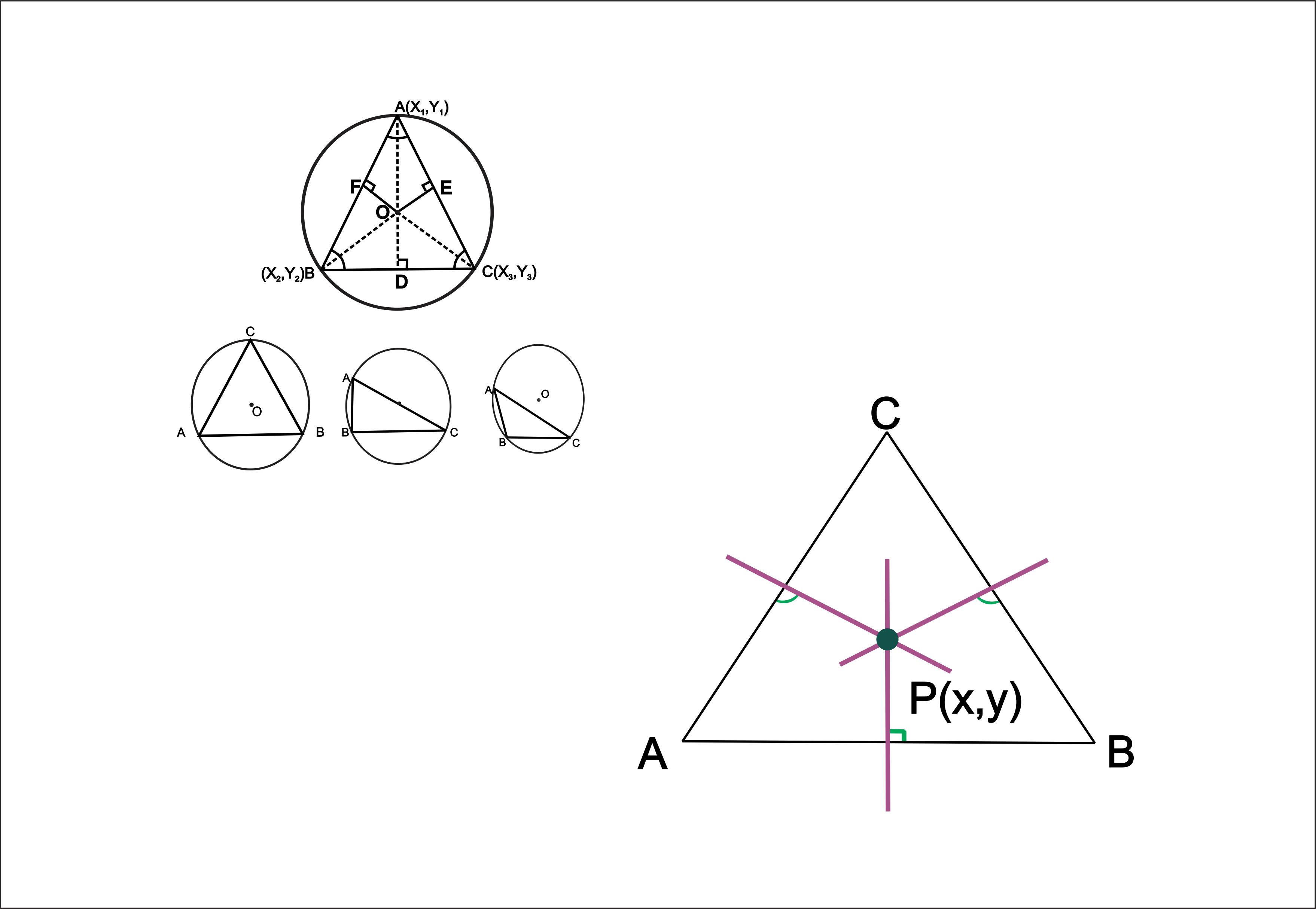
The co-ordinates of the centroid of the triangle whose vertices are `(x_1, y_1 ), (x_2, y_2)` and `(x_3, y_3)` is
`((x_1 +x_2 +x_3)/3, (y_1 +y_2 +y_3)/3)`
Please see the image,
Let `A= (x_1, y_1), B = (x_2, y_2 )` and `C = (x_3, y_3) .`
Then the co-ordinates of `D` will be `D = ((x_2 +x_3)/2, (y_2 +y_3)/2)`
The co-ordinate of a point dividing `AD` in the ratio `2 : 1` are
`((2((x_2+x_3)/2)+1.x_1)/(2+1), (2((y_2+y_3)/2)+1.y_1)/(2+1))
= ((x_1+x_2+x_3)/3, (y_1+y_2+y_3)/3)`
Similarly the co-ordinate of a point dividing `BE, CF` in the ratio `2 : 1` will also be same due to symmetry.
Hence medians of a triangle are concurrent and the co-ordinates of the centroid are
`((x_1+x_2+x_3)/3, (y_1+y_2+y_3)/3)`
Fundas :
`=>` The centroid is always located inside the triangle.
`=>` The centroid divides each median in a ratio of `2 : 1.`
`=>` Each median divides a triangle into the two triangles of equal areas.
`=>` Centroid of a triangle joining the middle points of a triangle is same as that of original triangle.
`=>` The area of `DeltaGBC, DeltaGCA, DeltaGAB` are equal.
`=>` Centroid is also centre of gravity of triangle
`=>` To find the centroid of any other shape, find the centre of gravity of that image,
e.g centroid of a circle and rectangle are centre and point of intersection of diagonals respectively.
The point of intersection of the medians of a triangle is called the Centroid of the triangle.
Median is the line joining `A` with middle point of `BC (D).` `( AD` , `BE` and `CF` are Medians in the image )
Medians are concurrent and point of intersection of Medians divides median in ratio of `2 : 1`
The co-ordinates of the centroid of the triangle whose vertices are `(x_1, y_1 ), (x_2, y_2)` and `(x_3, y_3)` is
`((x_1 +x_2 +x_3)/3, (y_1 +y_2 +y_3)/3)`
Please see the image,
Let `A= (x_1, y_1), B = (x_2, y_2 )` and `C = (x_3, y_3) .`
Then the co-ordinates of `D` will be `D = ((x_2 +x_3)/2, (y_2 +y_3)/2)`
The co-ordinate of a point dividing `AD` in the ratio `2 : 1` are
`((2((x_2+x_3)/2)+1.x_1)/(2+1), (2((y_2+y_3)/2)+1.y_1)/(2+1))
= ((x_1+x_2+x_3)/3, (y_1+y_2+y_3)/3)`
Similarly the co-ordinate of a point dividing `BE, CF` in the ratio `2 : 1` will also be same due to symmetry.
Hence medians of a triangle are concurrent and the co-ordinates of the centroid are
`((x_1+x_2+x_3)/3, (y_1+y_2+y_3)/3)`
Fundas :
`=>` The centroid is always located inside the triangle.
`=>` The centroid divides each median in a ratio of `2 : 1.`
`=>` Each median divides a triangle into the two triangles of equal areas.
`=>` Centroid of a triangle joining the middle points of a triangle is same as that of original triangle.
`=>` The area of `DeltaGBC, DeltaGCA, DeltaGAB` are equal.
`=>` Centroid is also centre of gravity of triangle
`=>` To find the centroid of any other shape, find the centre of gravity of that image,
e.g centroid of a circle and rectangle are centre and point of intersection of diagonals respectively.