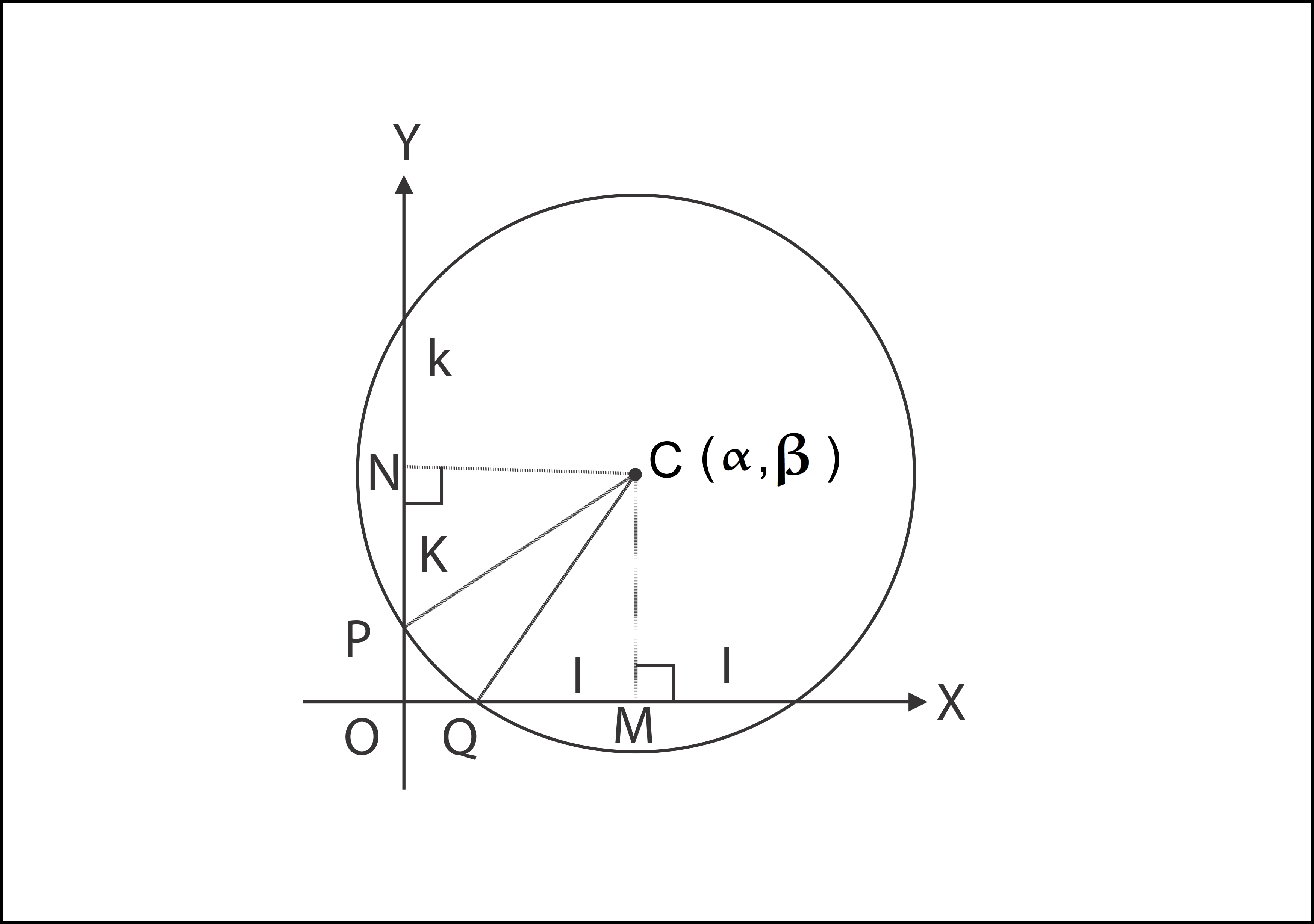Mathematics VARIOUS FORMS OF EQUATIONS OF A CIRCLE
Please Wait... While Loading Full Video

VARIOUS FORMS OF EQUATIONS OF A CIRCLE

BASIC OF CIRCLE - Geometry ( Xth Class)

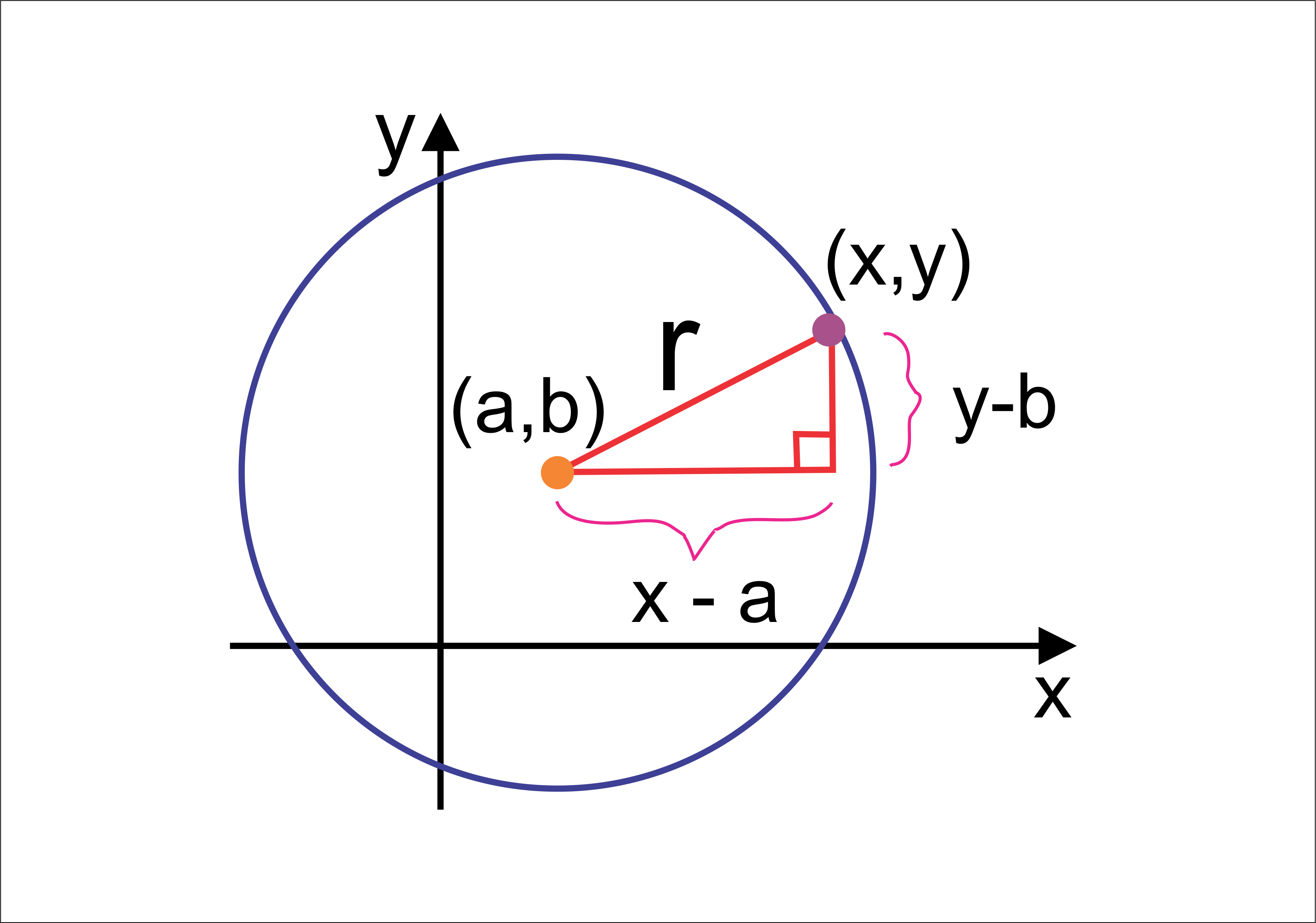
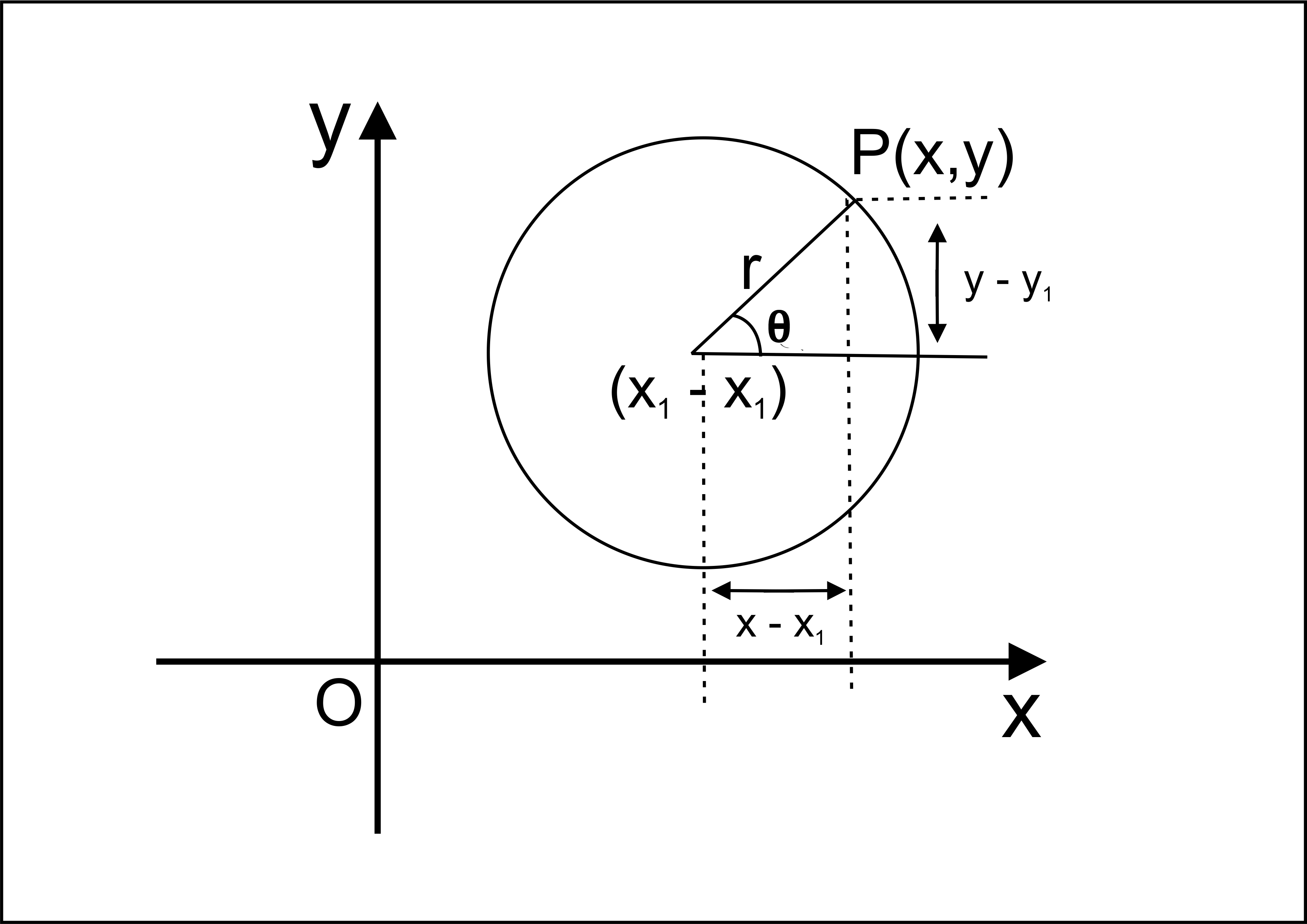
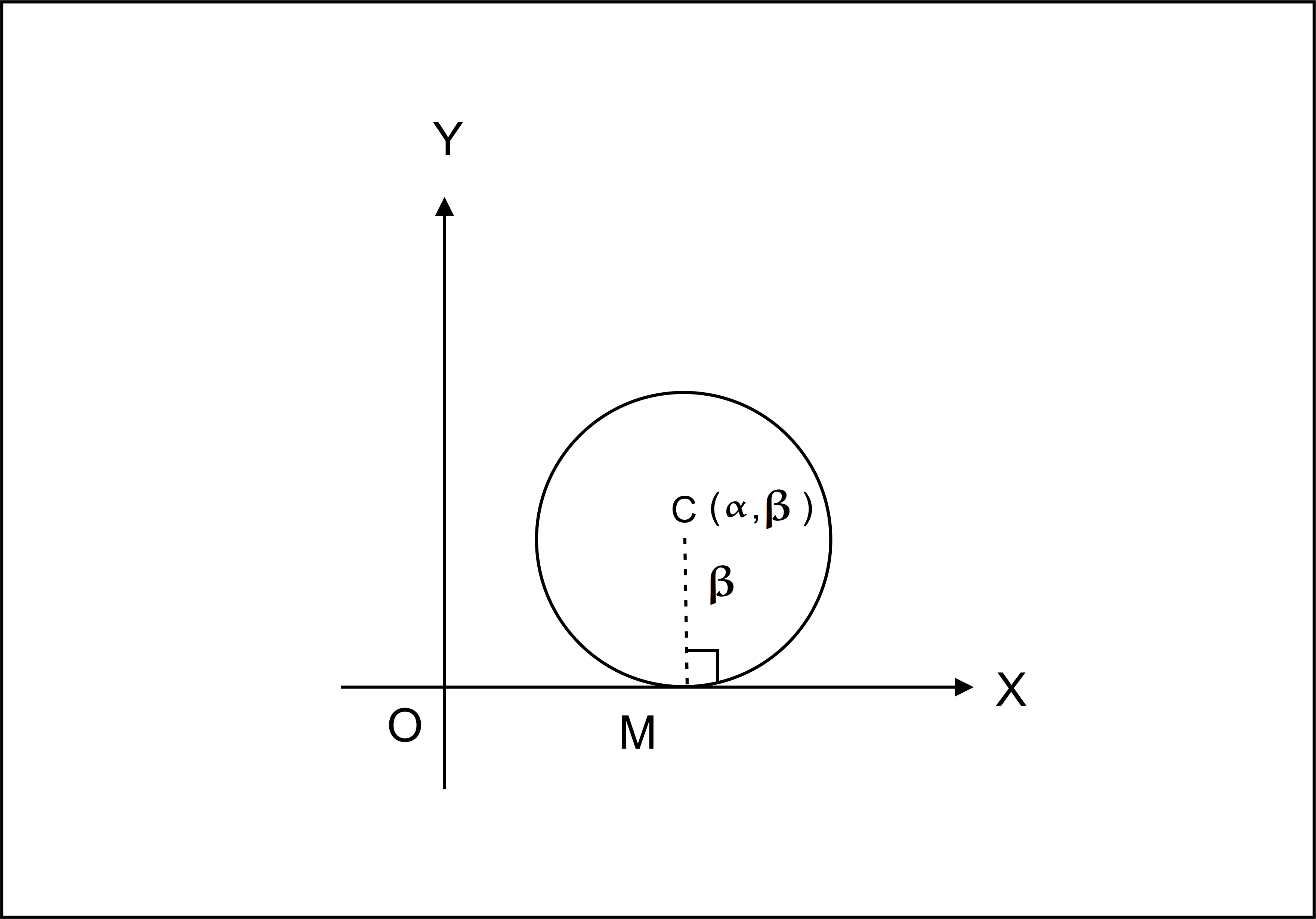
`text(DEFINITION :)` A circle is the locus of a point which moves in a plane, so that its distance from a fixed point in the plane is always constant.

The fixed point is called the centre of the circle and the constant distance is called its radius.

`text(CP =constant distance = Radius)`

`text(Chord and Diameter :)` The line joining any two points on the circumference is called a chord. If any chord passing through its centre is called its diameter.

`AB =`Chord, `PQ =` Diameter

where `C` is centre of the circle.


`1.` Equal chords subtends equal angles at the centre and vice-versa.


`2.` Equal chords of a circle are equidistant from the centre and vice-versa.


`3.` Angle subtended by an arc at the centre is double the angle subtended at any point on the remaining part of the circle.

`4.` Angles in the same segment of a circle are equal.

`5.`The sum of the opposite angles of a cyclic quadrilateral

is `180^0` and vice-versa.

`6.` lf a line touches a circle and from the point of contact a chord is

drawn, the angles which this chord makes with the given line

are equal respectively to the angles formed in the corresponding alternate segments.

`7.` If two chords of a circle intersect either inside or outside the

circle, the rectangle contained by the parts one chord is equal in

area to the rectangle contained by the parts of the other.

`AP xx PB = CP xx PD`

`8.` The greater of the two chords in a circle is nearer to

the centre than lesser.

`9.` A chord drawn across the circular region divides it into parts

each of which is called a segment of the circle.

`10.` The tangents at the extremities of a chord of a circle are equal.


CENTRE RADIUS FORM

Let r be the radius and `C (a,b)` be the centre of any circle.

If `P (x, y)` be any point on the circumference.

Equation of a circle is essentially the equation of circumference of circle.

Then `CP =a`

`(CP)^2 = a^2`

`(x-a)^2 + (y -b)^2 =r^2`

This is Centre Radius form of equation

`text(Note:)` that this is not the standard equation of equation of circle

If centre is origin then equation `x^2 + y^2 = r^2` is called STANDARD equation of circle.

`x^2 + y^2 + 2gx + 2fy + c = 0 ` is GENRAL equation of circle.

GENERAL EQUATION OF A CIRCLE

General equation of the circle is taken as

`x^2 + y^2 + 2gx + 2fy + c = 0.`

This can be written as `(x + g)^2 + (y + f)^2 = (sqrt( g^2 + f^2 - c ))^2`

hence, Centre `= ( - g, - f)` i.e. `( -` coeffictent of `x/2, -` coeffictent of `y/2 )`

Radius `= sqrt( g^2 + f^2 - c )`

For above two Equations to be correct ensure that

the coefficients of `x^2` and `y^2` equal to `1` and right hand side equal to zero.

Funda 1 :

Necessary and sufficient condition for general equation of degree `2` i.e.

`ax^2 + 2hxy + by^2 + 2gx + 2fy + c = 0` to represent a circle is

(a) coefficient of `x^2` + coefficient of `y^2` (not necessarily unity) and

(b) coefficient of `xy=0`



Funda 2 :

The general equation of circle `x^2 + y^2 + 2gx + 2fy + c = 0` contains `3` independent arbitrary constants

`g, f` and `c`

To find the equation of a circle we need one of the following:

1) A unique circle passes through `3` non-collinear points hence co-ordiantes of `3` points on a circle or

2) `3` tangents to a circle or

3) Equation of `2` tangents to a circle and a point on the circle

etc..


Funda 3 :

Nature of circle:

`x^2 + y^2 + 2gx + 2y + c - 0`

where radius `= sqrt(g^2 + f^2 - c)`

Now the following cases are possible :

(i) If `g^2 + f^2- c > 0`,

then the radius of circle will be real. Hence in this case real circle is possible.

(ii) If `g^2 + f^2- c = 0`,

then the radius of circle will be real. Hence in this case,

circle is called a point circle.

(iiii) If `g^2 + f^2- c < 0`,

then the radius of circle will be imaginary number. Hence

in this case, circle is called a virtual circle or imaginary circle.

DIAMETER FORM OF A CIRCLE

The equation of the circle drawn on the straight line joining two given points

`(x_1, y_1)` and `(x_2, y_2)` as diameter is

`(x - x_1)(x -x_2) + (y - y_1)(y - y_2) = 0`

Let `A` and `B` be the extremities of the diameter `AB` having coordinates

`(x_1, y_1)` and `(x_1, y_2)` respectively. Let `P (x, y)` be any point on the circle.

Join `P, A` and `P, B`. Then

`m_1` = Slope of the line `AP = (y - y_1)/(x- x_1)`

`m_2` = slope of the line `BP = (y - y_2)/(x - x_2)`

Now, since the angle subtended at the point `P`

in the semicircle `APB` is a right angle

`:. m_1m_2 = -1 => (y - y_1)/(x - x_1) xx (y - y_2)/(x - x_2) = -1`

`=> (y - y_1)(y - y_2) = -x(x-x_1)( x- x_2)`

`=> (x - x_1) (x - x_2) + (y - y_1) (y - y_2) =0`

This is the required equation of the circle having `(x_1, y_1)` and `(x_2, y_2)` as

the coordinates of the end points of a diameter

PARAMETRIC EQUATION OF A CIRCLE

Let the equation of circle is

`(x - x_1)^2 + (y - y_1)^2 = r^2`, where centre is `(x_1, y_1)` & radius is `'r'` then , by diagram

If the radius of a circle whose centre is at C (0, 0) makes an angle `theta` with the
positive direction of x-axis, then `theta` is called the parameter.

`x- x_1 = r cos theta` and `y - y_1 = r sin theta`

or `x = x_1 + r cos theta ` and `y = y_1 + r sin theta`

` :. tt ((x = x_1 + r cos theta),(y= y_1 + r sin theta))` `rightarrow` Parametric equation of circle where `theta in[0 , 2pi)` is any parameter

Funda 1:

The parametric co-ordinates of any point on the circle
`(x - h)^2 + (y - k)^2 = a^2`
`P(x, y)` are given by` (h + a cos θ, k + a sin θ) theta in[0 , 2pi)`
and parametric equations of the circle

INTERCEPTS MADE ON AXES BY A CIRCLE

Solving the circle `x^2 + y^2 +2gx + 2fy + c = 0` with `y = 0` we get,

`x^2 + 2gx + c = 0` If discriminant `4(g^2 - c)` is positive, i.e., if

`g^2 > c`, the circle will meet the x-axis at two distinct points, say

`(x_1 , 0)` and `(x_2 , 0)` where `x_1 + x_2 = -2g` and `x_1x_2 = c`

The intercept made on x-axis by the circle

`=>|x_1 - x_2| = sqrt((x_1 + x_2)^2 - 4 x_1 x_2)`

Length of `x` intercept `= 2sqrt(g^2 - c)`

In the similar manner if `f^2 > c`,

Length of `y` intercept `= 2sqrt (f^2- c)`

Funda :

`(i) g^2-c >0 =>` circle cuts the x-axis at two distinct points.

`(ii) g^2 = c =>` circle touches the x-axis.

`(iii) g^2 < c =>` circle lies completely above or below the x-axis i.e. it does not intersect x-axis.

`(iv) f^2 -c >0 =>` circle cuts the y-axis at two distinct points.

`(v) f^2 = c =>` circle touches the y-axis.

`(vi) f^2 < c =>` circle lies completely on the right side or the left side of they-axis i.e. it does not intersect y-axis.


EQUATION OF CONCENTRIC CIRCLES

Two circles having the same centre `C` say `(h, k)` but different

radius `r_1`. and `r_2` respectively are called concentric circles. Thus the circles

`(x- h)^2 + (y - k)^2 = r_1^2` and `(x- h)^2 + (y - k)^2 = r_2^2` are concentric circles.

`text(NOTE :)` Therefore the equations of concentric circles differ only in constant terms.

THE CIRCLE PASSES THROUGH THE ORIGIN `(0,0)` AND HAS INTERCEPTS `2` AND `2beta` ON THE `x` -axis and `y`-axis RESPECTIVELY

Here, `OA = 2alpha, OB = 2beta`

then `OM = alpha` and `ON = beta`

Centre of the circle is `C(alpha, beta)` and radius

`OC = sqrt((alpha^2 + beta)^2)`

the equation of circle is

`(x- alpha)^2 +(y -beta)^2 = alpha^2 +beta^2`

or `x^2 +y^2 -2 alpha x - 2 beta y=0`

Note : If a circle is passing through origin, then constant term is absent i.e,

`x^2 + y^2 + 2gx + 2fy = 0 `

WHEN THE CIRCLE TOUCHES `x` -AXIS

Let `(alpha, beta)` be the centre of the circle, then radius `=|beta|`

`:.` equation of circle is `(x- alpha)^2 + (y - beta)^2 = beta^2`

`=> x^2 +y^2 -2alpha x - 2 beta y + alpha^2 =0`

Note : If the circle `x^2 +y^2 +2gx +2fy + c =0` touches the `x`- axis, then

`|-f| = sqrt(g^2 +f^2 -c)` or ` c =g^2`

WHEN THE CIRCLE TOUCHES `y`- AXIS

Let `(alpha, beta)` be the centre of the circle, then radius `= |alpha|`

`:.` equation of circle is `(x- alpha)^2 + (y - beta)^2 = alpha^2`

`=> x^2 +y^2 -2alpha x - 2 beta y + beta^2 =0`

Note : If the circle `x^2 +y^2 +2gx +2fy + c =0` touches the `y`- axis, then

`|-g| =sqrt(g^2 +f^2-c)`

or `c =f^2`

WHEN THE CIRCLE TOUCHES BOTH AXES

Here, `|OM| = | ON|`

Since length of tangents are equal from any point on circle.

`:.` Let centre is `(alpha, alpha)`

also radius `= alpha`

Equation of circle is `(x - alpha) ^2 + (y - alpha)^ 2 = alpha^ 2`

`=> x^ 2 + y ^2 - 2alpha x - 2alpha y + alpha^ 2 = 0 `

Note :-

1. If the circle `x^2 + y^2 + 2gx + 2fy + c = 0` touches both the axes, then

`|-g| = | -f| = sqrt(g^2 +f^2 -c)`

`:. c = g^2 = f^2`

`:. g =f = pm sqrt c`

`:.` Equation of circle is

`x^2 + y^2 pm 2sqrtc x pm 2 sqrtc y +c =0`

`=> (x pm sqrtc)^2 + ( y pm sqrt c )^2 =c^2`

2. If `alpha > 0` then centres for `I, II, III` and `IV` quadrants are `(alpha, alpha),(- alpha, alpha,),(- alpha,- alpha)` and `(alpha,- alpha)` respectively.

Then equation of circles in these quadrants are

`(x -alpha)^2 +(y -alpha)^2 = alpha^2, (x +alpha)^2 + (y - alpha)^2 = alpha^2`,

`(x +alpha)^2 +(y-alpha)^2 = alpha^2` and `(x -alpha)^2 + (y +alpha)^2 = alpha^2`, respectively.

WHEN THE CIRCLE TOUCHES `x`- AXIS AND CUT OFF INTERCEPTS ON `y`- AXIS OF LENGHT `2l`

Let centre be `(alpha, beta)`

`:.` radius `=beta`

`CQ = CN = beta`

In `triangle CMQ, beta = alpha +l^2, alpha = sqrt((beta^2 -l^2))` for `I` quadrant

`:.` Equation of circle is

`[x - sqrt((beta^2 -l^2))]^2 + (y - beta)^2 = beta^2`

Note : Length of intercepts on `y`-axis of the circle `x ^2 + y^ 2 + 2gx + 2fy + c = 0` is

`2l = 2sqrt((f^2 -c^2 ))`

i.e, and also circle touches `x`- axis

then `l^2 =f^2 -c`

`:. l^2 = f^2 - g^2 l^2 = (-f)^2 - (-g)^2`

`:.` locus of centre is `y^2 -x^2 =l^2` (rectangular hyperbola)

WHEN THE CIRCLE TOUCHES `y`- AXIS AND CUT OFF INTERCEPT ON `x` - AXIS OF LENGTH `2k`

Let centre be `(alpha, beta)`

`:.` radius `= alpha`

`CN = CQ = alpha`

`CN = CQ = alpha`

in `triangle CMQ`, `alpha^2 = beta^2 +k^2`

`beta = sqrt((alpha- k^2))` for `I` quadrant

`:.` Equation of circle is

`(x- alpha)^2 + (y - sqrt(alpha^2 -k^2))^2 = alpha^2`

Note : Length of intercept on `x`- axis of the circle `x^2 +y^2 +2gx + 2 fy + c =0` is

`2k = 2 sqrt((g^2 -c))`

i.e, `k^2 = g^2 -c`

and also circle touches `y`- axis

then `c=f^2`

` :. k^2 =g^2 -f^2 = (-g)^2 - (-f)^2`

`:.` locus of centre is `x^2 -y^2 =k^2` rectangular hyperbola

WHEN THE CIRCLE CUT OFF INTERCEPT ON `x`-AXIS AND `y`-AXIS OF LENGTH `2l` AND `2k` AND NOT PASSING THROUGH ORIGIN

Let centre be `(alpha, beta)`

`:.` radius `= CP + CQ = lamda` say

`(CP)^2 = (CQ)^2 =lamda^2`

`alpha^2+k^2 = beta^2 +l^2 =lamda^2`

`:. alpha = sqrt(lamda^2-k^2)` [for `I` quadrant]

and `beta = sqrt(lamda^2-l^2)`

`:.` Equation of circle is `(x - sqrt(lamda^2 -k^2))^2 + (y-sqrt(lamda^2 -l^2))^2 =lamda^2`

WHEN THE CIRCLE PASSES THROUGH THE ORIGIN AND CENTRE LIES ON `x` - AXIS

Let centre of circle be `C(a,0)`

`:.` radius `= a`

`:.` Equation of circle is

`(x-a)^2 +(y -0)^2 = a^2`

or `x^2 +y^2 -2ax =0`

WHEN THE CIRCLE PASSES THROUGH ORIGIN AND CENTRE LIES ON `y` - AXIS

Let centre of CIrcle be `C(0,a)`

`:.` radius `= a`

`:.` Equation of circle is

`(x -0)^2 +(y-a)^2 =a^2`

or `x^2 +y^2 -2ay =0`
 
SiteLock