Tangent to a Circle - Definition
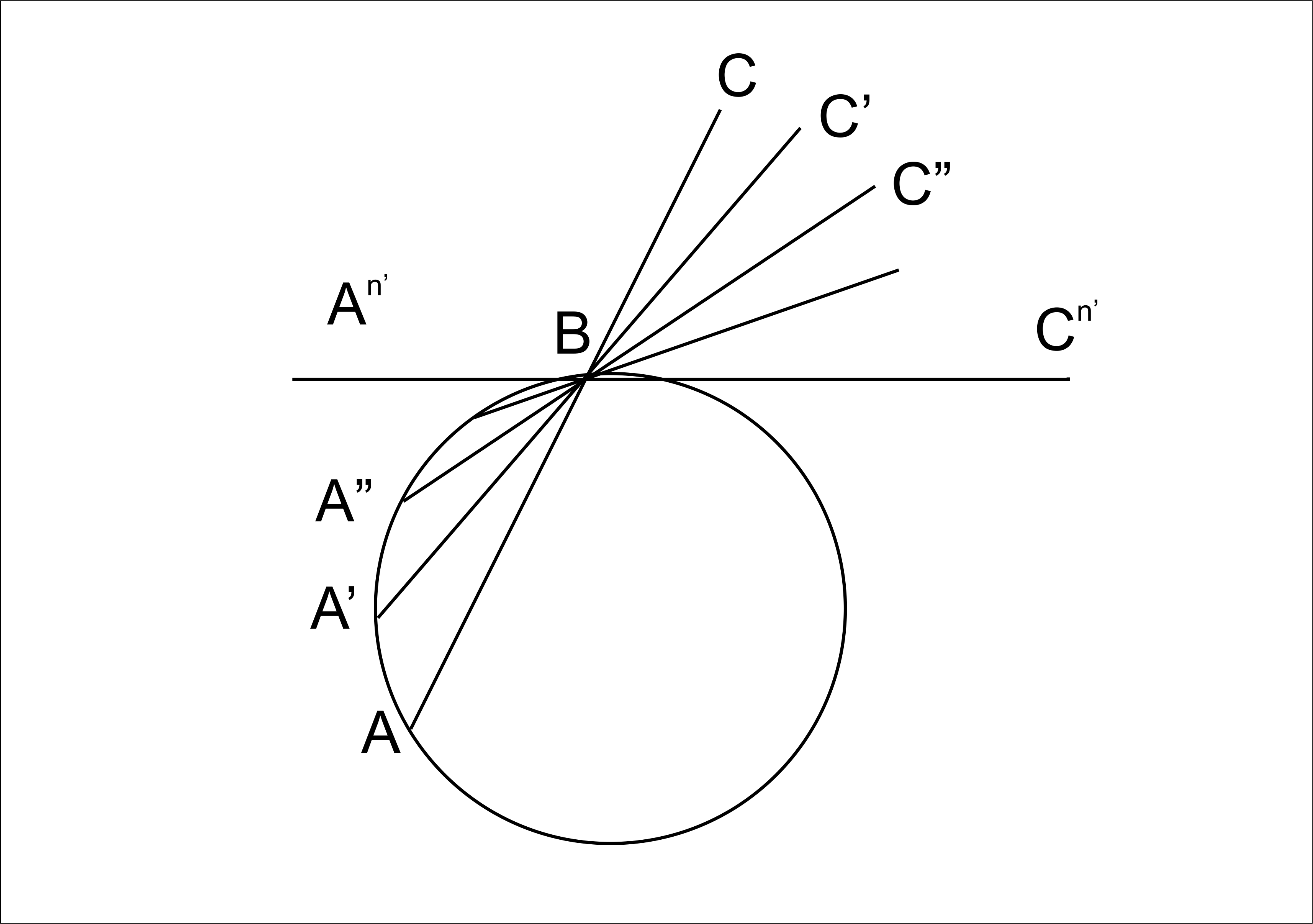
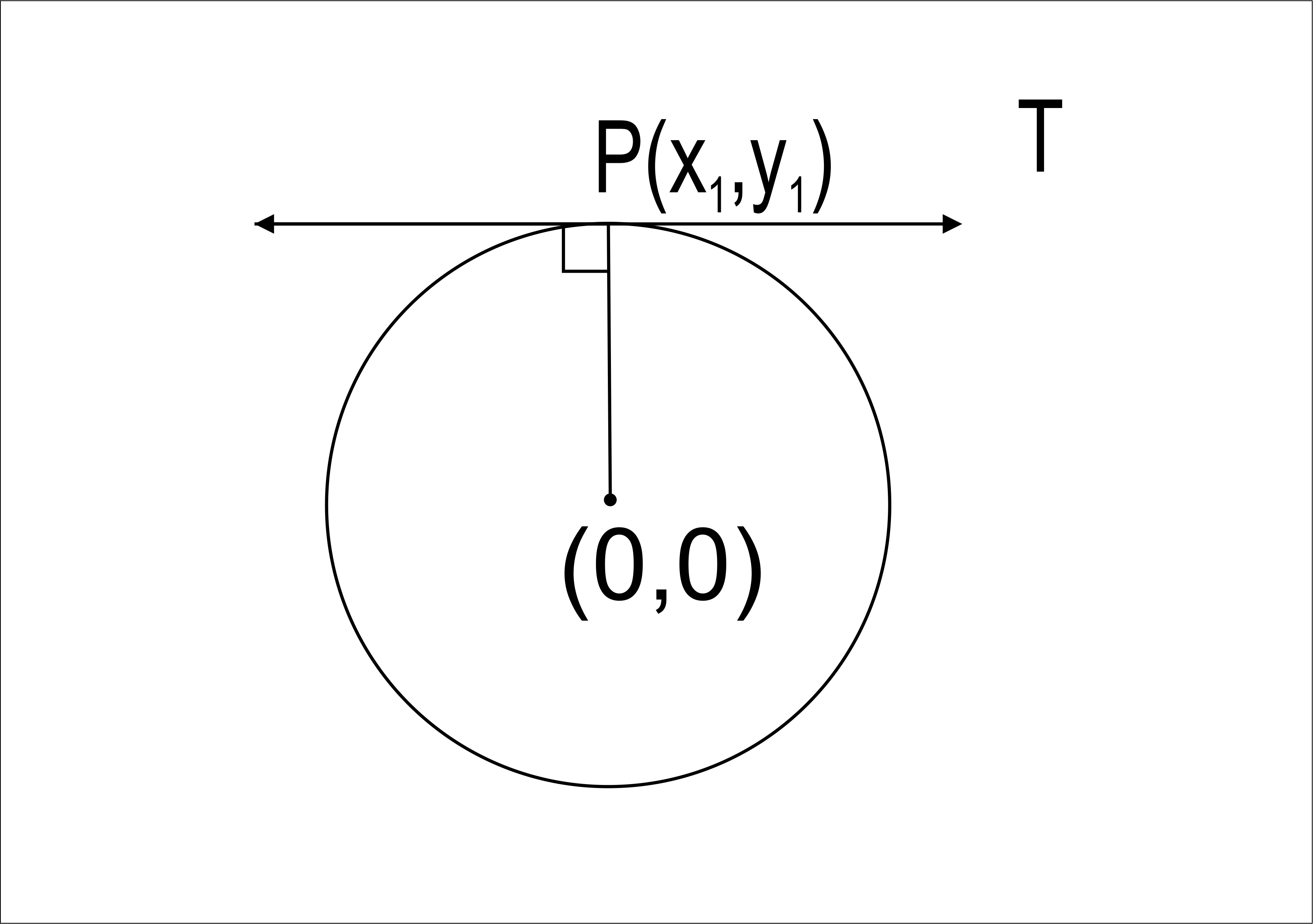
Let `A` and `B` be two points on the curve. Now point `A` is moving closer to point `B` along with the curve.
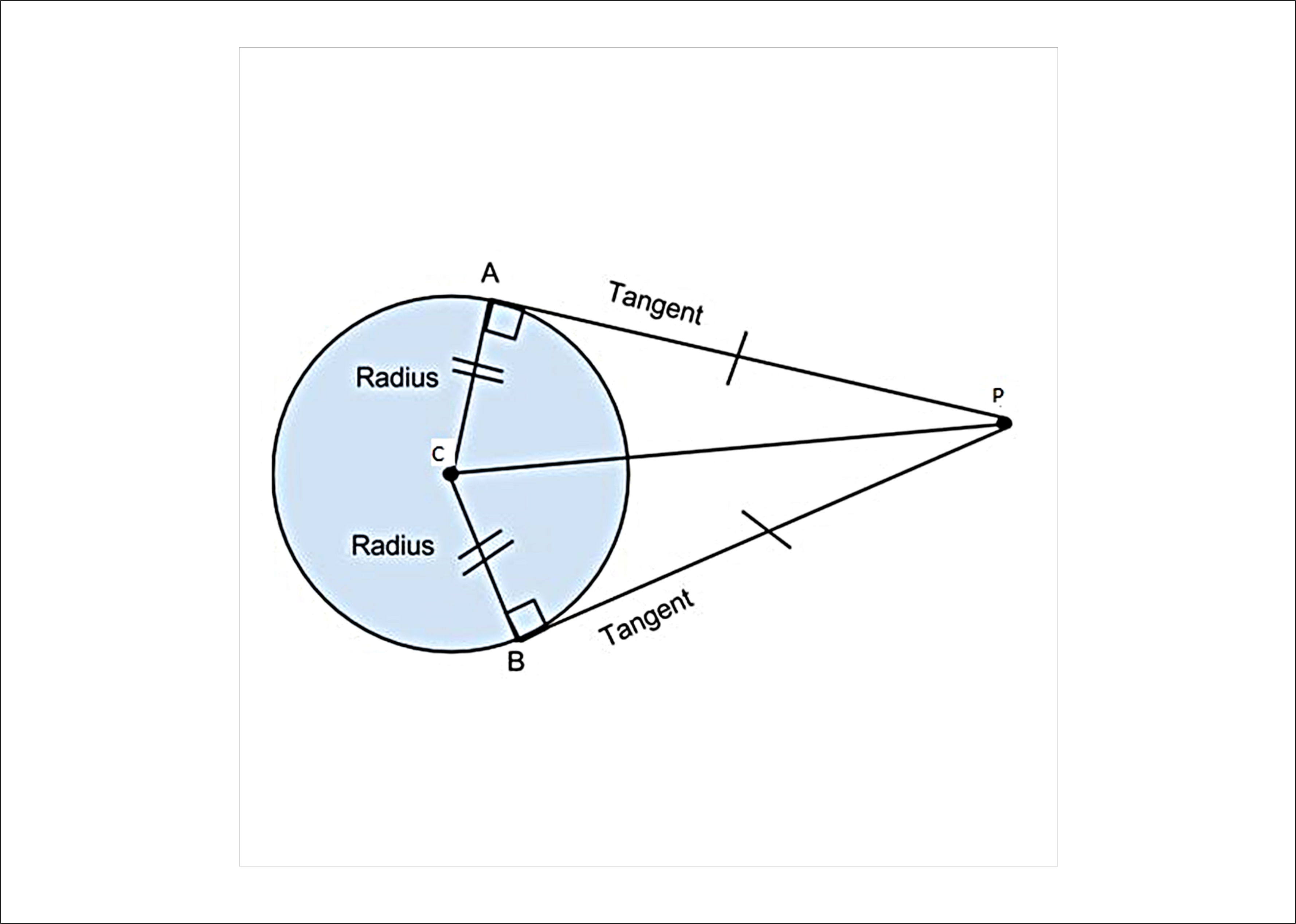
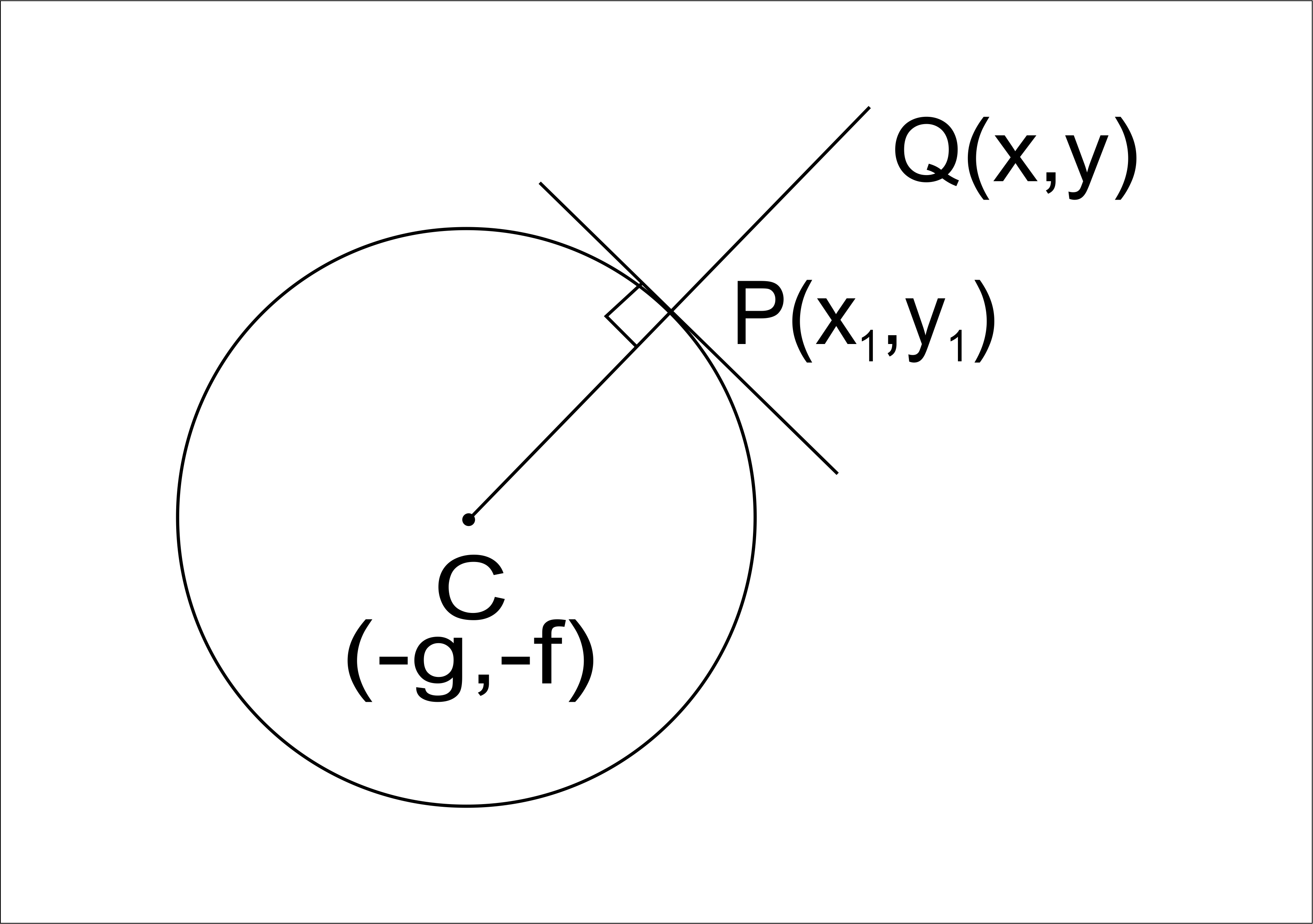
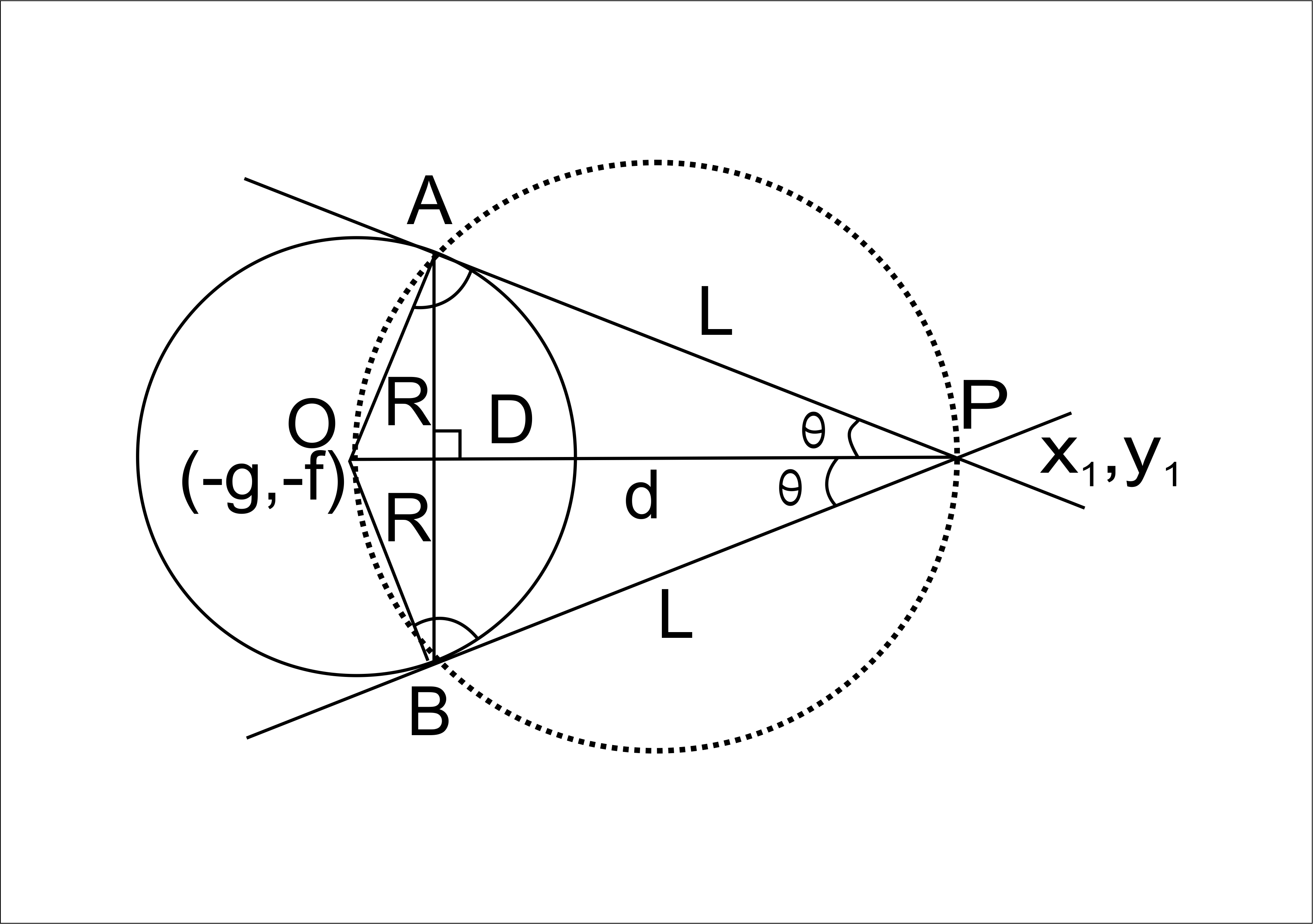
`AC` chord is changing the position accordingly soon as point `A rightarrow B`, chord `AC` (which is now `A^( n')c^(n')`) will become tangent to curve at point `B`.
This tangent is the limiting case of secant, point `B` is called point of contact of tangent
`AC` chord is changing the position accordingly soon as point `A rightarrow B`, chord `AC` (which is now `A^( n')c^(n')`) will become tangent to curve at point `B`.
This tangent is the limiting case of secant, point `B` is called point of contact of tangent