Mathematics CHORD, COMMON CHORD

Equation of Chord of Chord of contact

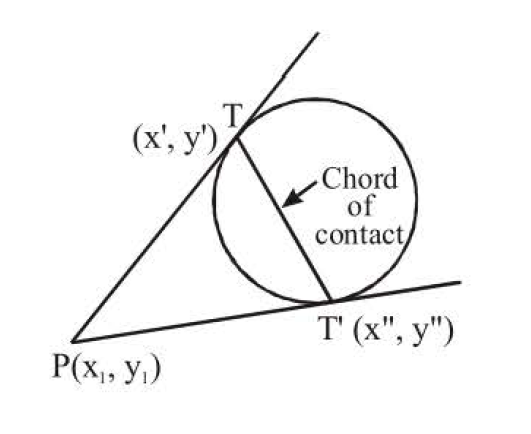
From any external point, two tangents can be drawn to a given circle. The chord joining the points of
contact of the two tangents is called the chord of contact of tangents.

The equation of the chord of contact of tangents drawn from a point `(x_1, y_1)` to the circle `x^2 + y^2 = a^2` is

`I x x' + yy' = a^2 ` or ` T = 0 `

Proof: Let `T(x', y')` and `T'(x" , y")` be the points of contact of tangents drawn from `P (x_1, y_1)` to `x^2 + y^2 = a^2`

Then equations of tangents `PT` and `PT'` are `x x' + yy' = a^2` and `x''+ y'' = a^2` respectively.

Since both tangents pass through `P (x_1, y_1)` then

`x_1 x' + y_1 y'= a^2`

and `x_1 x'' + y_1 y''= a^2`

Point `T (x', y')` and `T' (x", y")` lie on

`x x _1 + yy _1 = a^2`

:. Equation of chord of contact `T T'` is

`x x_1 + y y_1 = a^2`

Equation of Chord Bisected at a given Point

The equation of the chord of the circle `x^2 + y^2 = a^2` bisected at the point (`x_1,y_1`) is given by

`x x_1+yy_1-a^2 = x_1^2+y_1^2 - a^2` or `T = S`

Proof : Let any chord `AB` of the circle `x^2 + y^2 = a^2` be bisected at `D (x_1, y_1).`

If centre of circle is represented by `C`

then slope of `DC = (0-y_1)/(0-x_1) = y_1/x_1` ,

Slope of the chord `AB` is `- x_1/y_1`

then equation of `AB` is `y-y_1 = - x_1/y_1 (x-x_1)`

or `yy_1-y_1^2 = -x x_1 + x_1^2`

or `x x_1+yy_1+x_1^2 + y_1^2`

or `x x_1 +yy_1-a^2 = x_1^2 + y_1^2-a^2`

`T=S_1`

Equation of Chord in Parametric form

Consider the circle `x^2 + y^2 = a^2` with its centre at the origin `0` and of radius `'a'`, then the equation of chord
joining the two points whose parametric angle are `alpha` and `beta`

`(y-asinalpha)/(a(sinalpha - sinbeta)) = (x-acosalpha)/( a(cosalpha-cosbeta))` or

`x(sinalpha-sinbeta)-y(cosalpha-cosbeta)= a[sinalpha cosbeta- cosalpha sinbeta] = a sin (alpha+beta)`

or `2x sin((alpha - beta)/2) cos((alpha+beta)/2)+2ysin((alpha - beta)/2)sin((alpha + beta)/2)`

`= 2asin((alpha - beta)/2) cos((alpha - beta)/2)`

or ` xcos((alpha - beta)/2)+ysin((alpha + beta)/2) = a cos((alpha - beta)/2)`

COMMON CHORD OF TWO CIRCLES :

The chord joining the points of intersection of two given circles is called their common chord.

The equation of common chord of two circles

`S= x^2 + y^2 + 2g_1x +2f_1y+c_1 = 0`

`S'= x^2 + y^2 + 2g_2x +2f_2y+c_2 = 0`

`2 (g_1 - g_2)x + 2 (f_1 - f_2) y + c_1 - c_2 = 0`

or `S -S'=0`

`text(Proof :)`

`S = 0 ` and `S'= 0` be two intersecting circles

then `S -S'=0`

or `2 (g_1 - g_2)x + 2 (f_1 - f_2) y + c_1 - c_2 = 0` is a first degree equation in `x` and `y.`

So, it represent a straight line. Also, this equation satisfied by

the intersecting points of two given circles `S =0` and `S' = 0.`

Hence `S -S'=0` represents the common chord of circles `S =0` and `S' = 0.`

`text(Length of common chord :)`

We have `PQ = 2 PM` ` (-: M text(is mid point of) PQ)`

` quadquadquadquadquadquad=2sqrt({C_1P}^2-{C_1M}^2)`

Where `C_1P =` radius of the circle `S =0`

and `C_1M =` length of perpendicular from `C_1` on common chord `PQ.`

`text( Fundas :)`

`(i)` The common chord `PQ` of two cirlces becomes of the maximum length when it is a diameter of the smaller one between them.

`(ii)` Circle drawn on the common chord as a diameter then centre of the circle passing through `P` and `Q` lie on the common chord of two circles i.e. `S -S'=0`

`(iii)` If the length of common chord is zero, then the two circles touch each other and the common chord becomes the common tangent to the two circles at the common of contact.