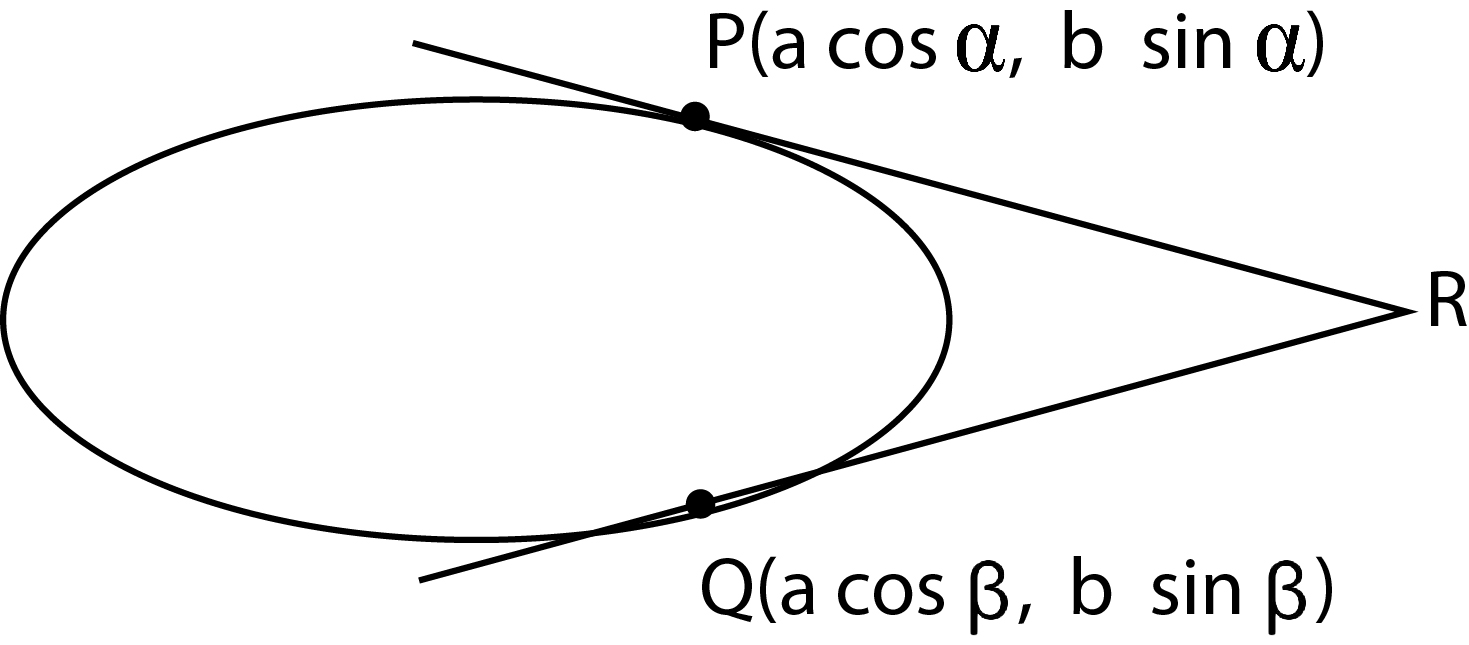
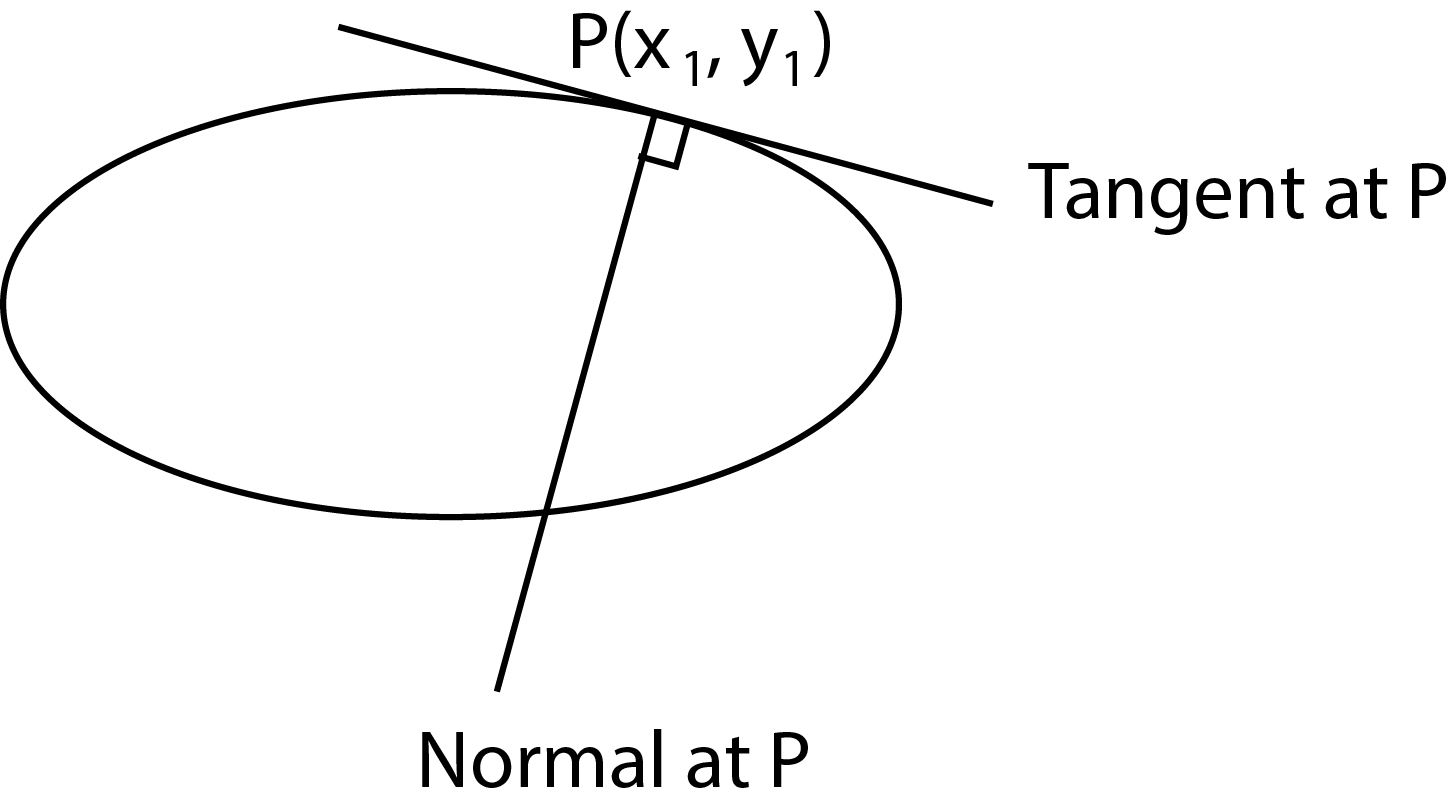
Tangents- Point Form :
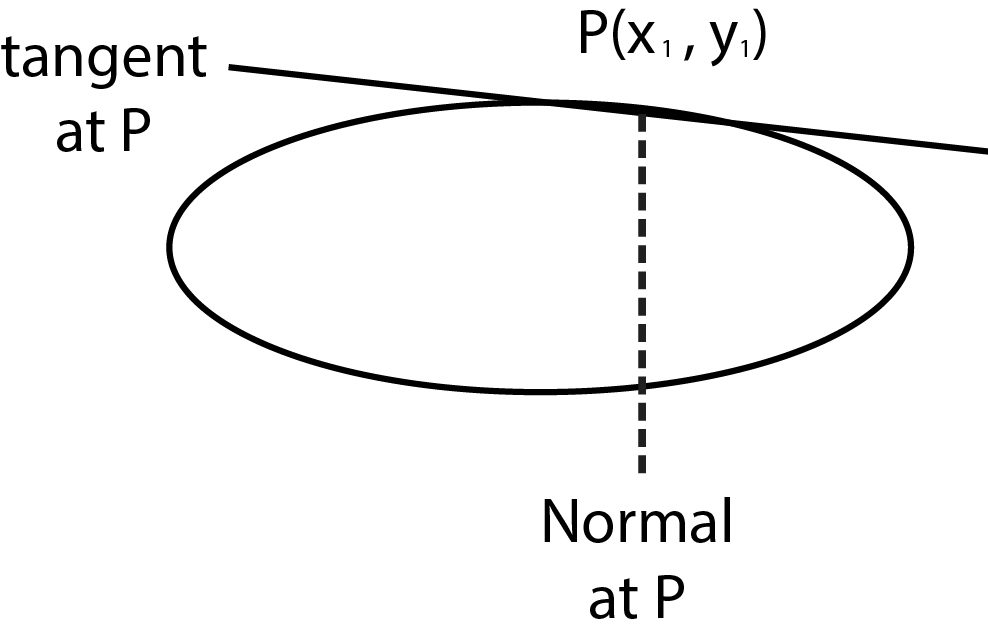
`(x x_1)/a^2+(y y_1)/b^2=1` is tangent to the ellipse at `(x_1 ,y_1)`.
Since point `(x_1 y_1)` lie on the curve therefore we can use standard substitution to obtain the equation of tangent.
Since point `(x_1 y_1)` lie on the curve therefore we can use standard substitution to obtain the equation of tangent.