Mathematics DIFFERENT FORMS OF EQUATION OF HYPERBOLA
Please Wait... While Loading Full Video

DIFFERENT FORMS OF EQUATION OF HYPERBOLA

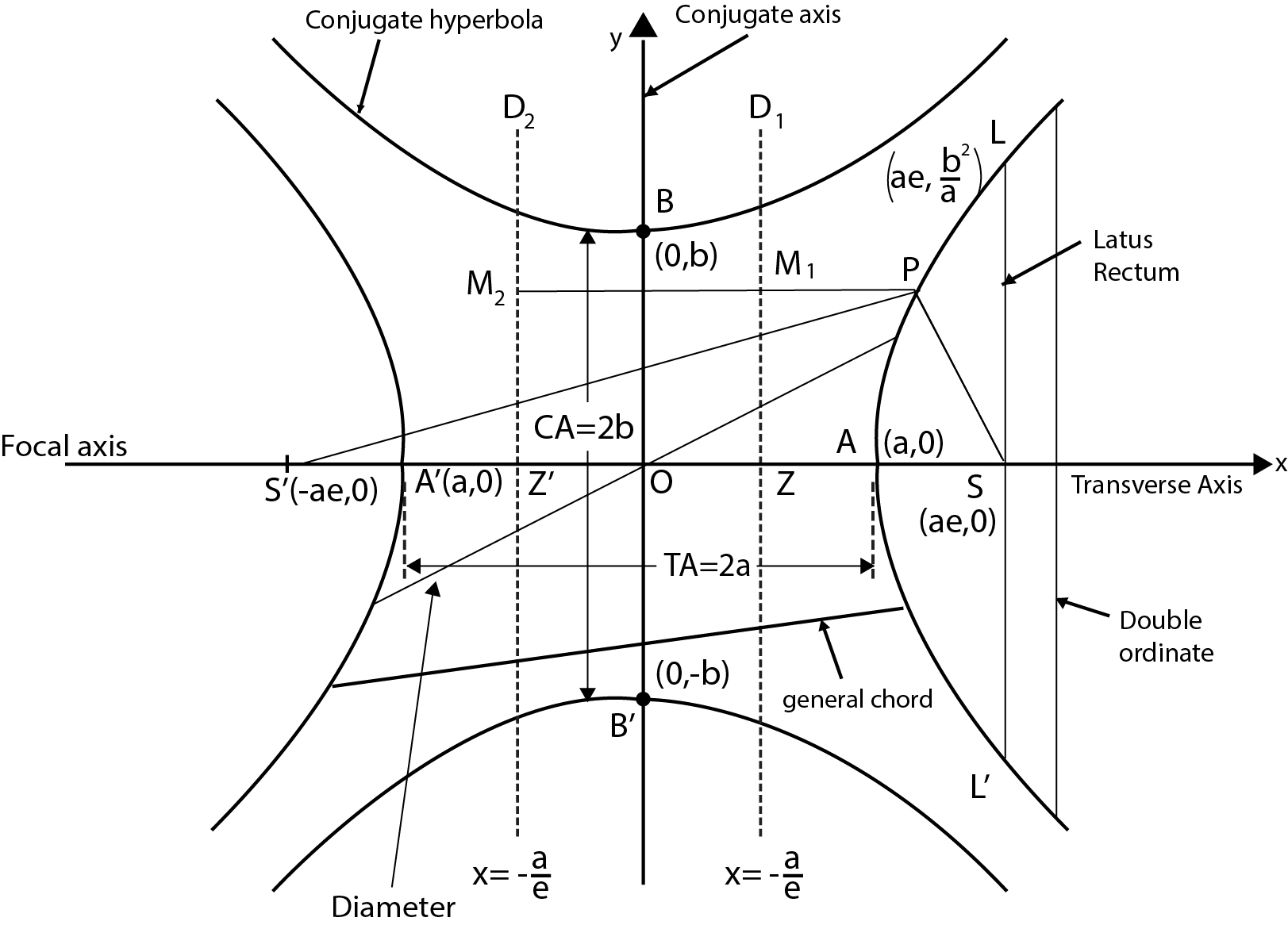
Definition of Hyperbola :

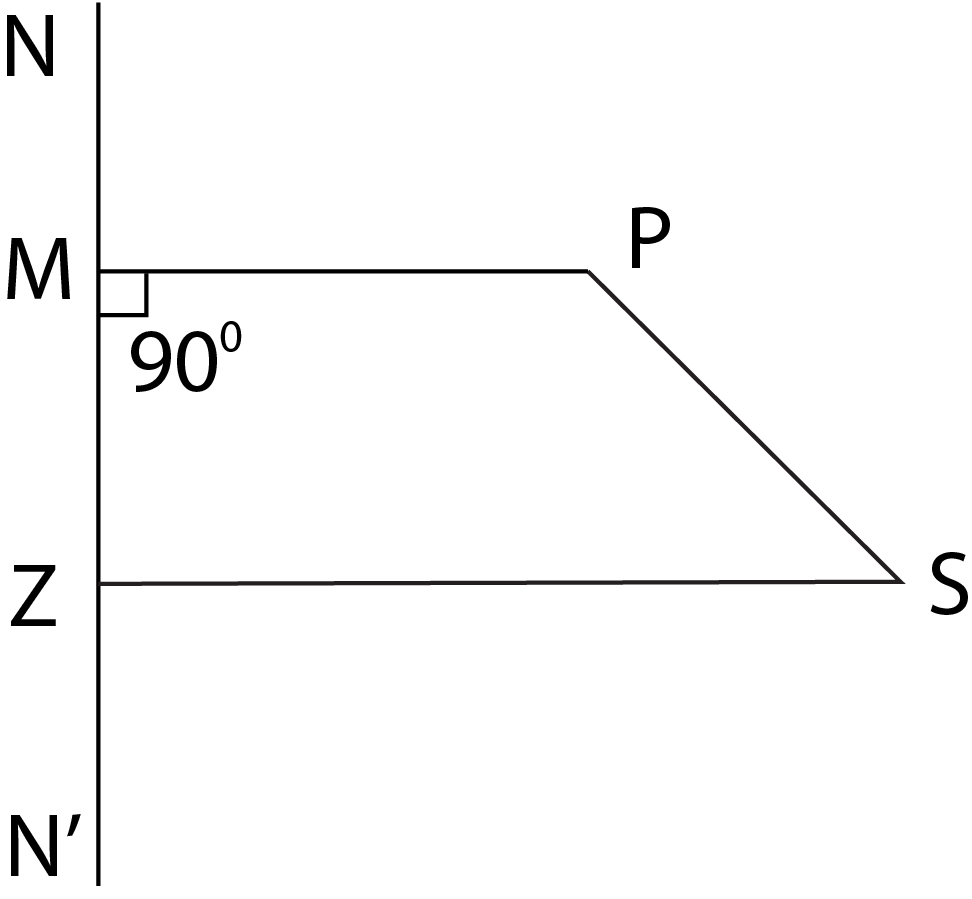
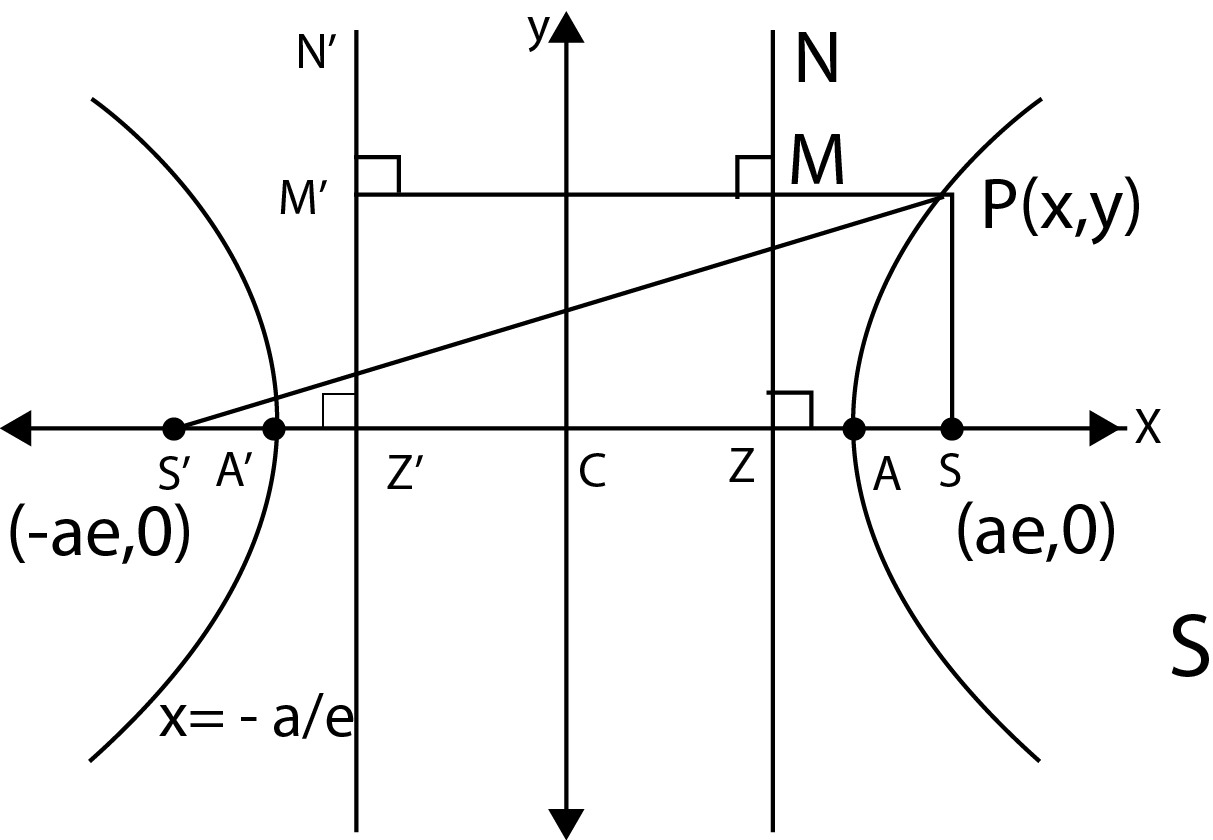
A hyperbola is the locus of a point which moves in a plane such that the ratio of its distance from a ftxed point and a given straight line is always constant.

The ftxed point is called the focus, the fixed line is called the directrix and the constant ratio is called the eccentricity of the hyperbola and denoted by `e`.

In the given figure, `S` is the focus and `N'N` the directrix.

Let `P` be any point on the hyperbola, then `PM = e, e > 1`.

Equation of a hyperbola can be obtained if the coordinates of its focus, equation of its directrix and eccentricity are given.

Standard Equation of a Hyperbola :

Let `S` be the focus & `ZN` is the directrix of an ellipse. Draw perpendicular from `S` to the directrix which meet it at `Z` . A moving point is on the hyperbola such that

`PS=ePM`

then there is point lies on the line `SZ` and which divide `SZ` intemally at `A` and extemally at `A'` in the ratio of `e: 1`.

therefore `SA = e AZ` ..... (i)

`SA' = eA'Z` ..... (ii)

Let `A A' = 2a` & take `C` as mid point of `A A'`

`:. CA = CA' = a`

Add `(i)` & `(ii)`

`SA + SA' = e (AZ + A'Z)`

`(CS - CA) + (CA' + CS) = e [CA - CZ + CA' + CZ]`

`2CS = 2e . CA`

`CS = a e`

Subtract `(ii)` & `(i)`, we get

`SA' - SA = e (A'Z - AZ)`

`(CA' + CS) - (CS - CA) = e [(CA' + CZ) - (CA - CZ)]`

`2CA = 2e . CZ => CZ = a/e`.

Consider `CZ` line as `x`-axis, `C` as origin & perpendicular to this line & passes through `C` is considered as `y`-axis. Now represent important parameters on coordinates plane. Let `P(x, y)` is a moving point, then

By definrion of ellipse.

`PS = ePM=> (PS)^2 = e^2 (PM)^2`

`=> (x - ae)^2 + (y - 0)^2 = e^2 (x -a/e)^2 => (x - ae)^2 + y^2 = (a - ex)^2`

`=> x^2 + a^2e^2 - 2xae + y^2 = a^2 + e^2x^2 - 2xae => x^2 ( 1 - e^2) + y^2 = a^2 (I - e^2)`

`=> x^2/a^2 +y^2/(a^2(1-e^2))=1`

or `x^2/a^2 -y^2/(a^2(1-e^2))=1`

where `b^2=a^2(e^2-1)`

Hence equation of hyperbola is `x^2/a^2-y^2/b^2=1` where `b^2 = a^2 ( e^2 - 1)`

Parametric Equation of The Hyperbola :

Let `x^2/a^2-y^2/b^2=1` be the hyperbola with centre `C` and transverse axis `A'A`.

Therefore circle drawn with centre ` C` and segment `A'A` as a diameter is called auxiliary circle of the hyperbola.

`:.` Equation of the auxiliary circle is

`x^2 + y^2 = a^2`

Let `P(x, y)` be any point on the hyperbola `x^2/a^2-y^2/b^2=1` .

Draw `PN` perpendicular to `x`-axis.

Let `NQ` be a tangent to the auxiliary circle `x^2 + y^2 = a^2` Join `CQ` and let `angle QCN = phi`

then `P` and `Q` are the corresponding points of the hyperbola and the auxiliary circle. Here `phi` is the eccentric angle of `P. ` `(0 le phi < 2 pi)`.

Since `Q = (a cos phi, a sin phi)`

Now `x = CN = CQ sec phi = sec phi . a`

`:. P(x, y) = (a sec phi, y)`

`:. P` lies on `x^2/a^2-y^2/b^2=1`

`:. (a^2 sec^2 phi)/a^2-y^2/b^2=1` or `y^2/b^2=sec^2 phi-1=tan^2 phi`

`:. y= pm b tan phi`

`:. y=b tan phi` (`P` lies in `1` quadrant)

The equations of `x = a sec phi` and `y= tan phi` are known as the parametric equations of the hyperbola.

Hyperbola At a Glance :

Parametric coordinates `x = a sec theta` and `y = b tan theta`
 
SiteLock