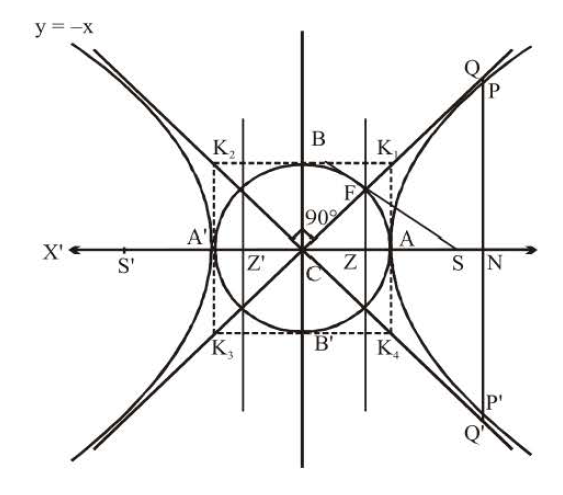
Asymptotes of Hyperbola :
If the length of the perpendicular let fall from a point on a hyperbola to a straight line tends to zero as the point on the hyperbola moves to infinity along the hyperbola, then the straight line is called the Asymptote of the Hyperbola.
In short asymptote is tangent to hyperbola at infinity.
Let `y = mx + c` is the asymptote of the hyperbola
`x^2/a^2=y^2/b^2=1`.
Solving these two we get the quadratic as
`(b^2- a^2m^2) x^2- 2a^2 mcx - a^2 (b^2 + c^2) = 0` ...... (1)
In order that `y = mx + c` be an asymptote, both roots of equation `(1)` must approach at infinity, the conditions for which are
coeff of `x^2 = 0` & coeff of `x = 0`.
`=> b^2 - a^2m^2 = 0` or `m = pm b/a` & `a^2 mc = 0=> c = 0`.
`:.` equations of asymptote are `x/a+y/b=0` and `x/a-y/b=0`
combined equation to the asymptotes `x^2/a^2-y^2/b^2=0`
As asymptotes of any hyperbola or a curve is a straight line which touches in it two points at infinity.
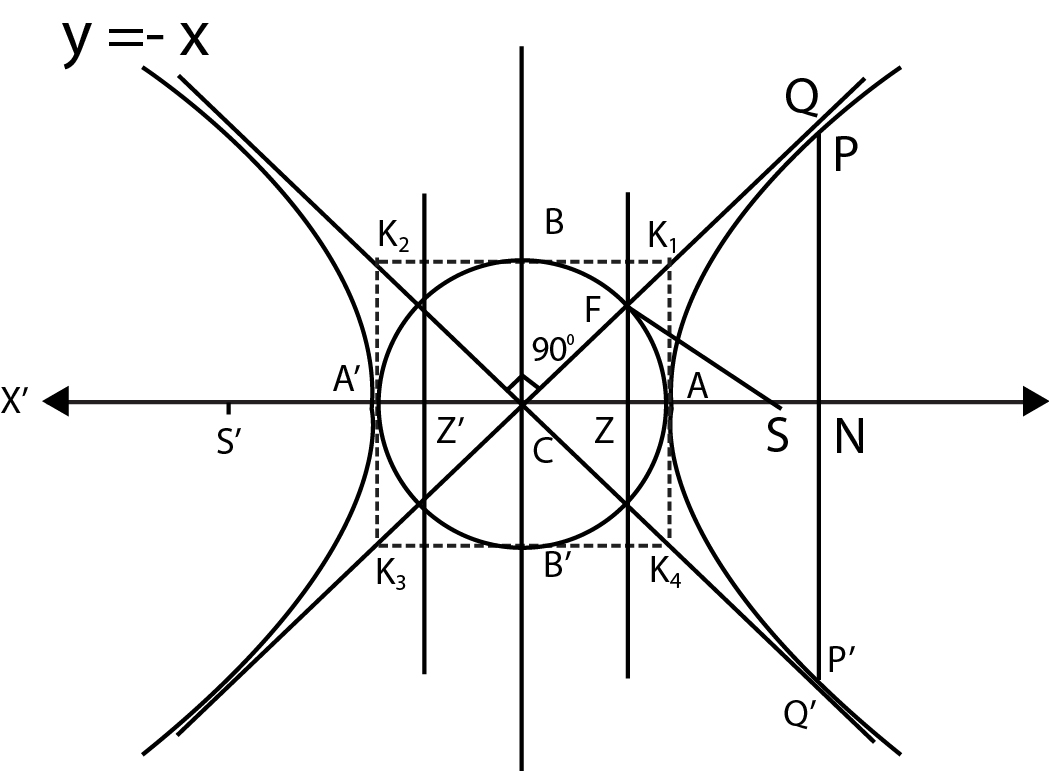
In short asymptote is tangent to hyperbola at infinity.
Let `y = mx + c` is the asymptote of the hyperbola
`x^2/a^2=y^2/b^2=1`.
Solving these two we get the quadratic as
`(b^2- a^2m^2) x^2- 2a^2 mcx - a^2 (b^2 + c^2) = 0` ...... (1)
In order that `y = mx + c` be an asymptote, both roots of equation `(1)` must approach at infinity, the conditions for which are
coeff of `x^2 = 0` & coeff of `x = 0`.
`=> b^2 - a^2m^2 = 0` or `m = pm b/a` & `a^2 mc = 0=> c = 0`.
`:.` equations of asymptote are `x/a+y/b=0` and `x/a-y/b=0`
combined equation to the asymptotes `x^2/a^2-y^2/b^2=0`
As asymptotes of any hyperbola or a curve is a straight line which touches in it two points at infinity.