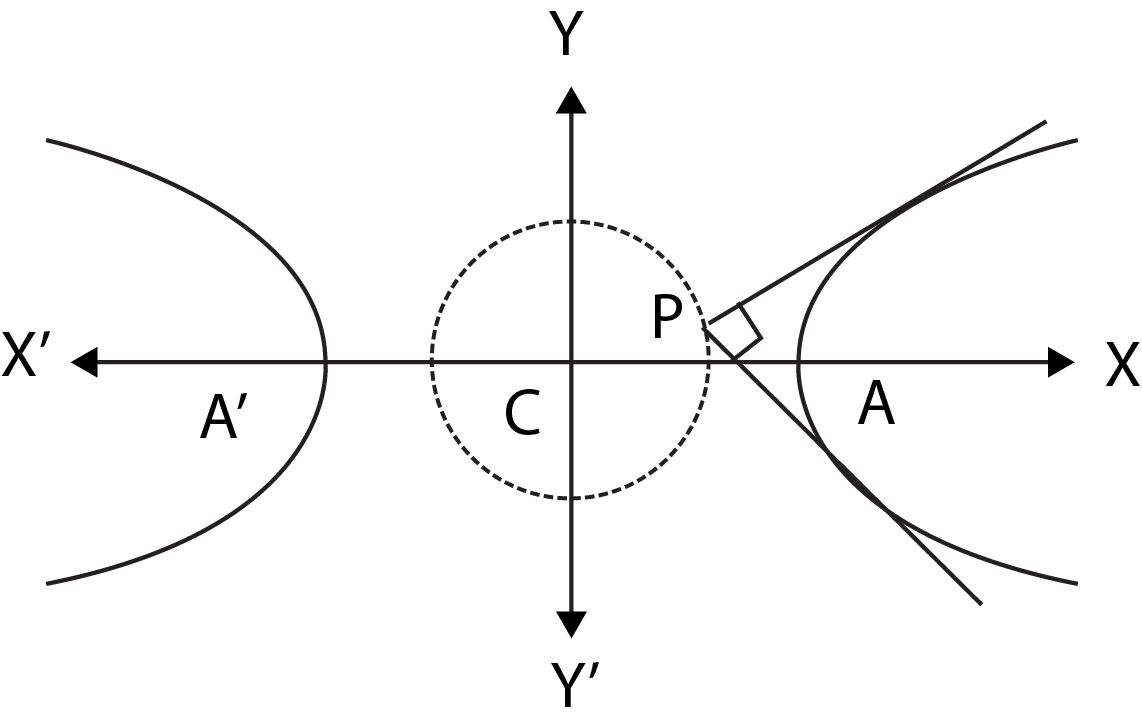
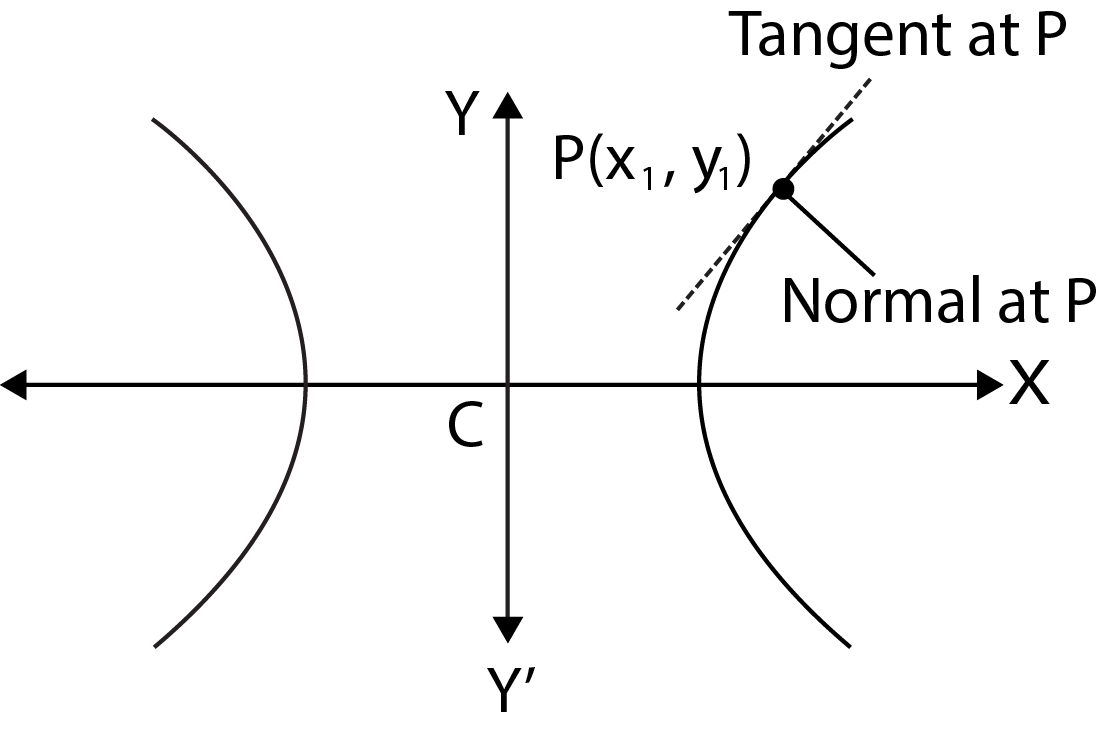
Equation of Tangent- Slope Form :
Given hyperbola is `x^2/a^2-y^2/b^2=1`.....................(1)
and the given line `y= mx +c` touches hyperbola then solve `(1) `and `(2)` , we get
`x^2/a^2-((mx+c)^2)/b^2=1` or `b^2x^2-a^2(mx+c)^2=a^2b^2`
or `(b^2 - a^2m^2) x^2 - 2a^2 mcx - a^2(c^2 + b^2) = 0`......................(3)
Since line `(2)` will be tangent to hyperbola `(1)`
if roots of equation `(3)` are equal i.e. `D = 0`
`4a^4m^2 c^2 + 4a^2(b^2 - a^2m^2) ( c^2 + b^2) = 0`
or `a^2m^2c^2 + b^2c^2 - a^2c^2m^2 + b^4 - a^2b^2m^2 = 0`
or `b^2c^2 + b^4 - a^2b^2m^2 = 0`
or `c^2+b^2- a^2m^2= 0`
or `c^2 = a^2m^2- b^2` or `c= pm sqrt(a^2m^2-b^2)`. This is the required condition of tangency.
and the given line `y= mx +c` touches hyperbola then solve `(1) `and `(2)` , we get
`x^2/a^2-((mx+c)^2)/b^2=1` or `b^2x^2-a^2(mx+c)^2=a^2b^2`
or `(b^2 - a^2m^2) x^2 - 2a^2 mcx - a^2(c^2 + b^2) = 0`......................(3)
Since line `(2)` will be tangent to hyperbola `(1)`
if roots of equation `(3)` are equal i.e. `D = 0`
`4a^4m^2 c^2 + 4a^2(b^2 - a^2m^2) ( c^2 + b^2) = 0`
or `a^2m^2c^2 + b^2c^2 - a^2c^2m^2 + b^4 - a^2b^2m^2 = 0`
or `b^2c^2 + b^4 - a^2b^2m^2 = 0`
or `c^2+b^2- a^2m^2= 0`
or `c^2 = a^2m^2- b^2` or `c= pm sqrt(a^2m^2-b^2)`. This is the required condition of tangency.