Mathematics DISTANCE BETWEEN POINTS & SECTION FORMULA
Please Wait... While Loading Full Video

DISTANCE BETWEEN POINTS & SECTION FORMULA

Distance Between Two Points :

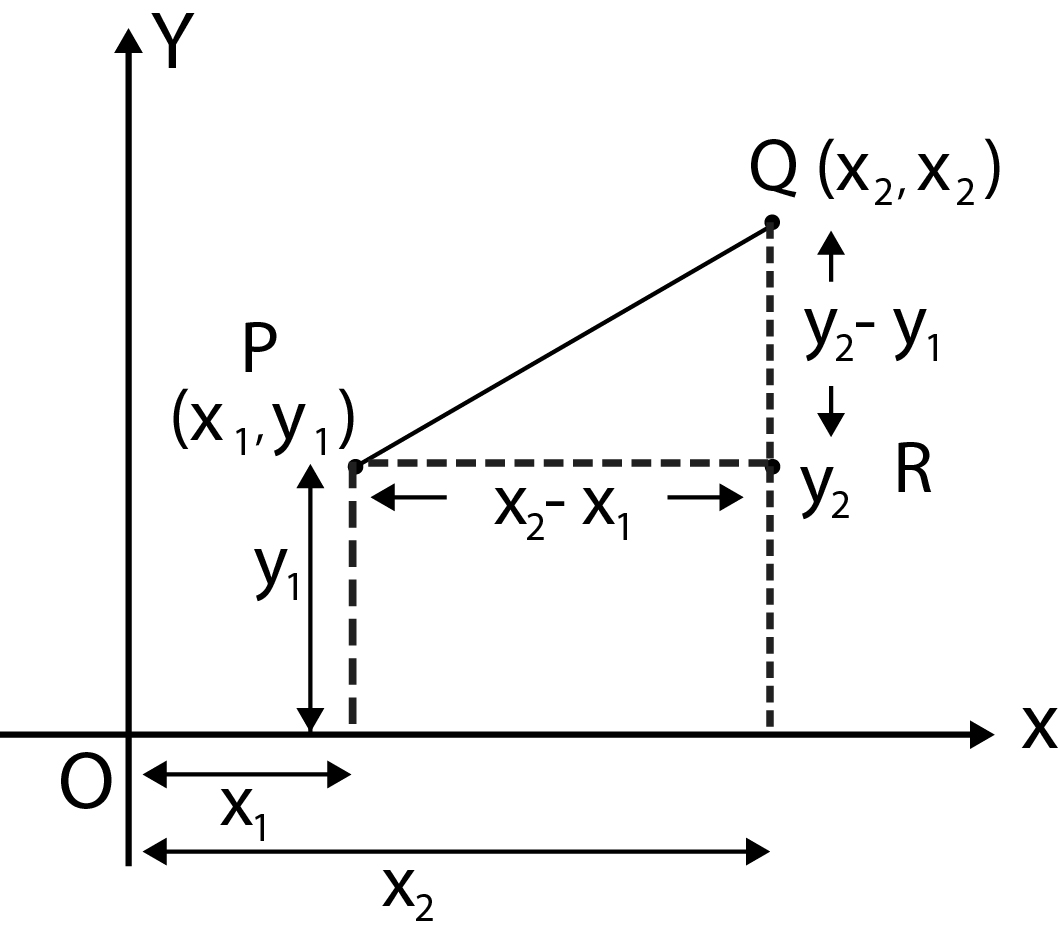
Let `P(x_1 ,y_1)` and `Q(x_2 y_2)` be two given points in the `xy` plane then distance between them is given by

`|PQ|=sqrt((x_1-x_2)^2+(y_2-y_1)^2)`

`text(Proof :)` For triangle `PQR`

`PQ^2 = PR^2 + RQ^2`

`quad quad quad quad quad = (x_2 - x_1)^2 + (y_2 - y_1)^2`

`|PQ|=sqrt((x_2-x_1)^2+(y_2-y_1)^2)`

`text(Note:)` Distance of `(x_1, y_1)` from origin `=sqrt(x_1^2+y_1^2)`

Internal Ratio Division

`triangle PQA` and `triangle BPC` are similar because

`angle PAQ`=`angle BCP` and `angle BCP`=`angle PQA`= `90^0`

Given `(PA)/(PB)=m_1/m_2` as per the properties of similar triangle

`(PA)/(BP) =(AQ)/(PC)=(PQ)/(BC)`

`m_1/m_2`=`(x-x_1)/(x_2-x_1)=(y-y_1)/(y_2-y_1)`

`(x,y)=((m_1x_2+m_2x_1)/(m_1+m_2),(m_1y_2+m_2y_1)/(m_1+m_2))`

divides the ratio by `m_2 ` and we will get coordinates as

`(x,y)=((m_1/ m_2x_2+x_1)/(m_1/ m_2 +1),(m_1/ m_2 y_2+y_1)/(m_1/ m_2 +1))`

Let `m_1/ m_2`=`lamda`

`(x,y)=((lamdax_2+x_1)/(lamda +1),(lamda y_2+y_1)/(lamda +1))`

These formula are knows as the internal Ratio Division formula.

External Ratio Division

The coordinates of the point dividing the line segment joining

`(x_1, y_1)` and `(x_2, y_2) ` in the ratio `m_1/ m_2`

`triangle PQA` and `triangle ABD` are similar because

`angle BAQ` is common and `angle AQP`=`angle ADB`= `90^0`

`(AB)/(PB)=m_1/m_2`

as per the properties of similar triangle

`(AB)/(AP) =(AQ)/(AD)=(BD)/(PQ)`

`m_1/m_1-m_2`=`(x-x_1)/(x_2-x_1)=(y-y_1)/(y_2-y_1)`

`(x,y)=((m_1x_2-m_2x_1)/(m_1-m_2),(m_1y_2-m_2y_1)/(m_1-m_2))`

divides the ratio by `m_2 ` and we will get coordinates as

`(x,y)=((m_1/ m_2x_2-x_1)/(m_1/ m_2 -1),(m_1/ m_2 y_2-y_1)/(m_1/ m_2 -1))`

Let `m_1/ m_2`=`lamda`

`(x,y)=((lamdax_2-x_1)/(lamda -1),(lamda y_2-y_1)/(lamda -1))`

These formula are knows as the External Ratio Division formula.

Harmonic Conjugates :

If two points `P` and `Q` divides the line `AB` internally and externally in the sarne rario `m:n` , then `P` and `Q` are said to be harmonic conjugate of each other with respect to `A` and `B`.

i.e., `(AP)/(PB)=(AQ)/(BQ)=lambda`.......................(1)

Also, `AP, AB` and `AQ` are in `H.P.` ie. `2/(AB)=1/(AP)+1/(AQ)`

Proof: from `(1)`,

`(AP)/(AB-AP)=(AQ)/(AQ-AB)`

`(AB-AP)/(AP)=(AQ-AB)/(AQ)`

`(AB)/(AP)-1=1-(AB)/(AQ)`

`2/(AB)=1/(AP)+1/(AQ)`
 
SiteLock