The set of all possible results of a random experiment is called the sample space of that experiment and it is generally denoted by `S .`
Each element of a sample space is called a sample point.
For example,
(i) If we toss a coin, there are two possible results, namely a head (H) or a tail (T). So, the sample space in this experiment is given by S =: {H, T}
(ii) When two coins are tossed, the sample space
S = { HH, HT, TH, TT}
where, HH denotes the head on the first coin and head on the second coin. Similarly, HT denotes the head on the first coin and tail on the second coin.

`text(Outcomes :)`

A possible result of a random experiment is called its outcome.

Consider the experiment of rolling a die. The outcomes of this experiment are `1, 2, 3, 4, 5` or `6`, if we are interested in the number of dots on the upper face of the die.

The set of outcomes `{1 , 2, 3, 4, 5, 6}` is called the sample space of the experiment. Thus, the set of all possible outcomes of a random experiment is called the sample space associated with the experiment. Sample space is denoted by the symbol `S`.
Each element of the sample space is called a sample point. In other words, each outcome of the random experiment is also called sample point.

`text(Event Definition)`

Any subset `E` of a sample space `S` is called an event.

Note : The maximum number of events which can be associated with an experiment is `2^n`, where n is the number of elements in the sample space.

i.e., `text()^nC_0+ text()^nC_1 + text()^nC_2 + .... + text()^nC_n = 2^n`


`text(Occurrence of an event :)`

Consider the experiment of throwing a die. Let `E` denotes the event" a number less than `4` appears". If actually `'I'` had appeared on the die then we say that event `E` has occurred. As a matter of fact if outcomes are `2` or `3,` we say that even `E` has occurred.

Thus, the event `E` of a sample space `S` is said to have occurred if the outcome `w` of the experiment is such that `w in E`. If the outcome `w` is such that `w notin E`, we say that the event `E` has not occurred.

`text(Impossible and Sure Events :)`

The empty set `phi` and the sample space `S` describe events. In fact `phi` is called an impossible event and `S` , i.e., the whole sample space is called the sure event.

To understand these let us consider the experiment of rolling a die. The associated sample space is
`S = {1, 2, 3, 4, 5, 6}`

Let `E` be the event" the number appears on the die is a multiple of `7"`.

Clearly no outcome satisfies the condition given in the event, i.e., no element of the sample space ensure the occurrence of the event `E`. Thus, we say that the empty set only correspond to the event `E`. In other words we can say that it is impossible to have a multiple of `7` on the upper face of the die. Thus, the event
`E = phi` is an impossible event.

Now let us take up another event `F` "the number turns up is odd or even". Clearly `F= {1 , 2, 3, 4, 5, 6}= S`,
i.e., all outcomes of the experiment ensure the occurrence of the event `F`. Thus, the event `F = S` is a sure event.


`text(Simple Event :)`

If an event `E` has only one sample point of a sample space, it is called a simple (or elementary) event In a sample space containing n distinct elements, there are exactly `n` simple events.

`S = {HH, HT, TH, T T}`

There are four simple events corresponding of this sample space. These are

`E_1={HH},E_2={HT},E_3={TH}` and `E_4={T T}`.


`text(Compound Event :)`

If an event has more than one sample point, it is called a compound event.

For example, in the experiment of "tossing a coin thrice" the events

`E` : 'Exactly one head appeared'

`F` : 'Atleast one head appeared'

`G`: 'Atmost one head appeared' etc.

are all compound events. The subsets of associated with these events are

`E = {HT T, THT, T TH}`
`F = {HT T, THT, T TH, HHT, HTH, THH, HHH}`
`G = {T T T, THT, HT T, T TH}`

Each of the above subsets contain more than one sample point, hence they are all compound events.


`text(Complementary Event :)`

For every event `A`, there corresponds another event `A'` or `A` called the complementary event to `A`. It is also called the event 'not `A'`.

For example, take the experiment 'of tossing three coins'. An associated sample space is

`S = {HHH, HHT, HTH, THH, HT T, THT, TTH, T T T}`

Let `A= {HTH, HHT, TH H}` be the event 'only one tail appears'.

Clearly for the outcome `HT T`, the event `A` has not occurred. But we may say that the event 'not `A'` has occurred. Thus, with every outcome which is not in `A`,we say that 'not `A`' occurs. Thus the complementary event 'not `A`' to the event `A` is

`A'= {HHH, HT T, THT, T TH, TIT}`

or `A' = `{ `w : w in S` and `w notin A`} `= S - A .`


`text(Independent Events)`

Two events are said to be independent, if the occurrence of one does not
depend on the occurrence of the other.
For example, When an unbiased die is thrown, then the sample space
`S = {1, 2, 3, 4, 5, 6}`
Let `E_1 = {1, 3, 5} :::` the event of occurrence of an odd number
and `E_2 = { 2, 4, 6} =` the event of occurrence of an even number.
Clearly, the occurrence of odd number does not depend on the occurrence of
even number.
So, `E_1` and `E_2` are independent events.

`=>` If `E_1` and `E_2` areindependent events, then
(a) `E_1` and `bar(E_2)` are independent events.
(b) `bar(E_1)` and `E_2` are independent events.
(c) `bar(E_1)` and `bar(E_2)` are independent events.

The probability of an event E to occur is the ratio of the number of cases in its favour to the total number of cases (equally likely).

`p (E)= (n(E))/(n(S))` = Number of cases favourable to event n(E) /n (S) Total number of cases

`text(Range of Value of)`` \P(f)`

Probability of occurrence of an event is a number lying between 0 and 1.

Proof Let S be the sample space and E be an event. Then,

`E subseteq S`

also `phi subseteq S`

where `phi` is a null set.

From Eqs. (i) and (ii), we get

`phi subseteq S supseteq E`

=> `n(phi) <= n(E) <=n(S)` => `0 <= P(E)<=1`

`text(Note :)` If E is any event and E' be the complement of event E, then

`P(E) + P(E') = 1`


`text(Odds in Favour and Odds Against the Event)`

Let S be the sample space. If a is the number of cases favourable to the event E, b is the number of cases favourable to the event E', the odds in favour of E are defined by a : b and odds against of E are b: a.
i.e., odds in favour of event E is

`a/b = (n(E))/(n(E')) = ((n(E))/(n(S)))/((n(E'))/(n(S))) = (p(E))/(p(E'))`

`(p(E'))/(p(E)) = b/a`

`(p(E'))/(p(E)) + 1 = b/a + 1`

`1/(p(E)) = (b+a)/a`

`p(E) = a/(a+b)` and `p(E')= b/(a+b)`

`text(Funda :)`

=> Use the sign `'+'` for the operation 'or' and `'x'` for the operation 'and' in order to the problems on definition of probability

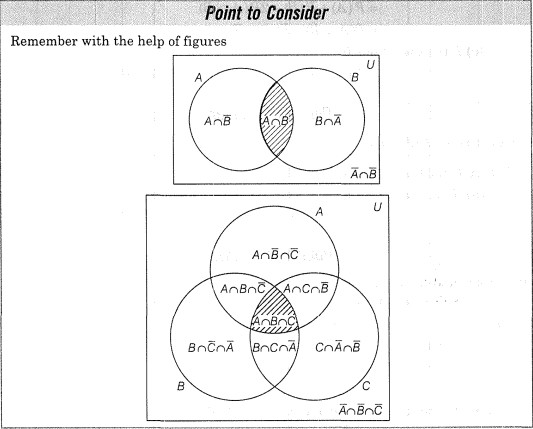
In the Chapter on Sets, we have studied about different ways of combining two or more sets, viz, union, intersection, difference, complement of a set etc. Like-wise we can combine two or more events by using the analogous set notations.
Let `A, B, C` be events associated with an experiment whose sample space is `S`.

`text(Some Important Symbols)`

If `A, B` and `C` are any three events, then
`(i) A nn B` or `AB` denotes the event of simultaneous occurrence of both the
events `A` and `B`.
`(ii) A uu B` or `A+ B` denotes the event of occurrence of atleast one of the
events A or B.
(iii) A- B denotes the occurrence of event A but not B.
(iv) `barA` denotes the not occurrence of event A.
(v) `A nn barB` denotes the occurrence of event A but not B.
(vi) `barA nn barB = bar(A uu B)` denotes the occurrence of neither A nor B.
(vii) `A uu B uu C` denotes the occurrence of atleast one event A, B or C.
(viii) `(A nn barB) uu (barA nn B)` denotes the occurrence of exactly one of A and B.
(ix) `A nn B nn C` denotes the occurrence of all three A, B and C.
(x) `(A nn B nn barC) uu (A nn barB nn C) uu (barA nn B nn C)` denotes the occurrence of
exactly two of A, B and C.

`text(Some Important Results)`

`(i)` A and Bare mutually exclusive events, then `A nn B = phi`. Hence, `P (A nn B) = 0`.
`therefore P(A uu B)= P(A) + P(B)`

`(ii) P (A uu B) = 1 - P (A nn B)`

`(iii)` If A, Band Care mutually exclusive events, then
`A nn B = phi , B nn C = phi, C nn A = phi, A nn B nn C = phi`
`=> P (A nn B) = 0, P (B nn C) = 0,`
`P (C nn A) = 0, P (A nn B nn C) = 0`
`P(A uu B uu C) = P(A) + P(B) + P(C)`

`(iv)` If `A_1, A_2, .... ,A_n` are mutually exclusive events, then

`sum_(i < j) P(A_i nn A_j ) =0. sum_(i < j < h) P(A_i nn A_j nn A_k)=0` and `p(A_1 nn A_2 nn .... A_n)=0`
`therefore P(A_1 uu A_2 uu .....uu A_n) = sum_(i = 1)^n p(A_i)`

`(v)` (a) P (atleast two of A, B, C occur)
`= P(A nn B) + P(B nn C)+ P(C nn A) - 2P(A nn B nn C)`
(b) P (exactly two of A, B, C occur)
`= P (A nn B) + P (B nn C) + P ( C nn A) - 3P (A nn B nn C)`
(c) P (exactly one of A, B, C occur)
`= P(A) + P(B)+ P(C)- 2P(A nn B)- 2P(B nn C) - 2P ( C nn A)+ 3P (A nn B nn C)`

`(vi)` (a) If `A_1, A_2, ... , A_n` are independent events, then
`P(A_1 nn A_2 nn ... nn A_n)= P(A_1)P(A_2) ... P(A_n)`
(b) If `A1_, A2_ , .... , A_n` are mutually exclusive events, then
`P(A_1 uu A_2 uu ... uu A_n ) = P(A_1) + P(A_2) + ... + P(A_n)`
(c) If `A_1, A_2, .. , A_n` are exhaustive events, then `P(A_1 uu A_2 uu ... uu A_n)= 1`
(d) If `A_1, A_2, ... ,A_n` are mutually exclusive and exhaustive events, then
`P(A_1 uu A_2 nn ... nn A_n)= P(A_1) + P(A_2) + ... + P(A_n) = 1`

`(vii)` If `A_1, A_2 , ... , A_n` are n events, then
(a) `P(A_1 uu A_2 uu ... uu A_n ) <= P(A_1) + P(A_2) + ... + P(A_n)`
(b) `P(A_1 nn A_2 nn ... nn A_n ) >= 1- P(A_1)- P(barA_2)- ... - P(barA_n)`