Mathematics ALGEBRA OF COMPLEX NUMBER : ADDITION, MULTIPLICATION,CONJUGATION

Algebra of Complex Number :ADDITION, SUBTRACTION, MULTIPLICATION AND DIVISION

`(A)text (Equality of complex number :)`

Let there be two complex numbers `z_1 = x_1 + iy_1` and `z_2 = x_2 + iy_2`.

If `z_1=z_2` then `R e (z_1)=R e(z_2)` and `Im(z_1)= Im(z_2)`.

i.e., if `x_1+iy_1=x_2+iy_2`

`=> x_1=x_2` and `y_1=y_2` simultaneously.

`(B)text(Addition :)`

`z_1 + z_2 = (x_1 + iy_1) + (x_2 + iy_2) = (x_1 + x_2) + i (y_1 + y_2) in C` .

It is easy to oberve that the sum of two complex numbers is a complex number whose real (imaginary) part is the sum of the real (imaginary) parts of the given numbers:

`Re(z_1 + z_2) = Re(z_1) + Re(z_2)`;

`Im(z_1 + z_2) = Im(z_1) + Im(z_2)`

`(C)text(Subtraction :)`

`z_1-z_2=(x_1+iy_1)-(x_2+iy_2)=(x_1-x_2)+i(y_1-y_2) in C`

That is `Re(z_1-z_2)=Re(z_1)-Re(z_2)`;

`Im(z_1-z_2)=Im(z_1)-Im(z_2)`.

`(D)text(Multiplication :)`

`z_1 . z_2 = (x_1 + iy_1 )(x_2 + iy_2) = (x_1 x_2 - y_1 y_2) + i(x_1y_2 + x_2y_1) in C`.

In other words

`Re(z_1 . z_2) = Re(z_1) . Re(z_2) - Im(z_1) . Im(z_2)`

and `Im(z_1 . z_2) = Im(z_1) . Re(z_2) + Im(z_2) . Re(z_1)`

For a real number `A` and a complex number `z = x + iy`.

`lambda . z=lambda(x+iy)= lambda x+i lambda y in C`

is the product of a real number with a complex number. The following properties are obvious :

`(a)` `lambda (z_1 + z_2) = lambdaz_1 + lambdaz_2`

`(b)` `lambda_1 (lambda_2z) = (lambda_1 lambda_2)z`;

`(c)` `(lambda_1 + lambda_2)z = lambda_1z + lambda_2z` for all ` z, z_1, z_2 in C` and `lambda, lambda_1 , lambda_2 in R`.

Actually, relations `(a)` and `(c)` are special cases of the distributive law and relation `(b)` comes from the associative law of mulriplicarion for complex numbers.

`(E)text(Division of Complex Number :)`

Let `z_1=x_1+iy_1` & ` z_2=x_2+iy_2`

Then `z_1/z_2=(x_1+iy_1)/(x_2+iy_2) => ((x_1+iy_1)(x_2-y_2))/((x_2+iy_2)(x_2-iy_2))`

`=> ((x_1x_2+y_1y_2)+i(y_1x_2-x_1x_2-x_1y_2))/((x_2^2+y_2^2))`

`=>{(x_1x_2+y_1y_2)/(x_2^2+y_2^2)}+i{(y_1x_2-x_1y_2)/(x_2^2+y_2^2)}`

`z_1/z_2=> Re(z_1/z_2)+ iIm(z_1/z_2)`

`text(Properties of Algebraic Operations on Complex Numbers :)`

Let `z_1` , `z_2` and `z_3` be any three complex numbers. Then, their algebraic operations satisfy the following properties :

1. Properties of Addition of Complex Numbers
(i) Closure law `z_1 + z_2` is a complex number.
(ii) Commutative law `z_1 + z_2 = z_2 + z_1`
(iii) Associative law `(z_1 + z_2) + z_3 = z_1 + (z_2 + z_3)`
(iv) Additive identity `z + 0 = z = 0 + z,` then 0 is called the additive identity.
(v) Additive inverse - z is called the additive inverse of z i.e., `z + (- z) = 0.`

2. Properties of Multiplication of Complex Numbers
(i) Closure law `z_1 · z_2` is a complex number.
(ii) Commutative law `z_1· z_2 = z_2 · z_1`
(iii) Associative law `(z_1 · z_2) z_3 = z_1 (z_2 · z_3)`
(iv) Multiplicative identity `z · 1 = z = 1· z,` then 1 is called the multiplicative
identity.
(v) Multiplicative inverse If z is a non-zero complex number, then`1/z` is called
the multiplicative inverse of z i.e., z .

`1/z = z = 1/z .z`
(vi) Multiplication is distributive with respect to addition
`z_1 (z_2 + z_3) = z_1.z_2 + z_1.z_3`

Conjugate of Complex Number :

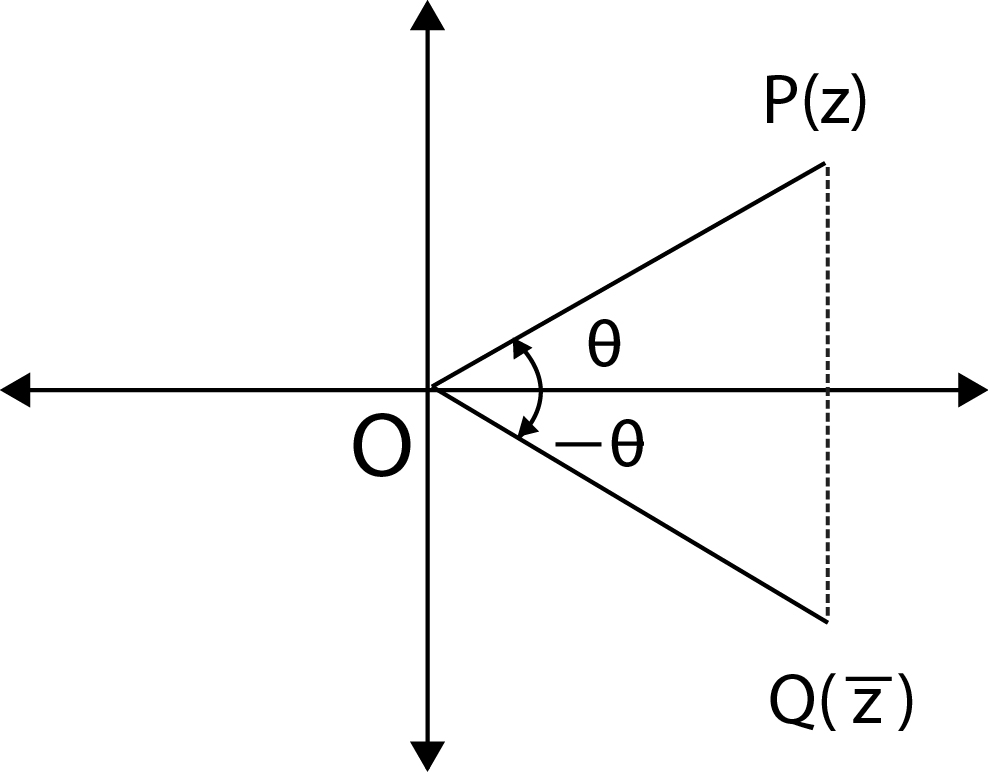
Conjugate of a complex number `z = a + i b` is denoted and defined by `z = a - i b`. ln a complex number if we replace `i` by `- i`, we get conjugate of the complex number. `z` is the mirror image of `bar z` about real axis on Argand's Plane.
Geometrical representation of conjugate of complex number

`text(Properties of Conjugate Complex Numbers :)`

Let `z, z_1` and `z_2` be complex numbers. Then,

`(i) bar(barz) = z`

`(ii) z + barz = 2Re(z)`

`(iii) z - barz = 2 Im (z)`

`(iv) z + barz = 0 => z = -- barz => z` is purely imaginary.

`(v) z- barz = 0 => z = barz => z` is purely real.

`(vi) bar(z_1 ± z_2) =barz_1 ± barz_2`
In general, `bar(z_1 ± z_2 ± z_3 ± ... ± z_n) = barz_1 ± barz_2 ± barz_3 ± ... ± barz_n`

`(vii) bar(z_1 · z_2) = barz_1 · barz_2`
In general, `bar(z_1 · z_2 · z_3 ... z_n) = barz_1 · barz_2 · barz_3 ... barz_n`

`(viii) (barz_1/z_2) = barz_1/z_2 , z_2 ne 0`

`(ix) barz^n = (barz)^n`

`(x) z_1.barz_2 + barz_1z_2 = 2 Re(z_1,barz_2)`

`(xi ) z bar z=a^2 +b^2 = |z|^2 ,` where `z=a+ib`

Dot and Cross Product :

Let `z_1 = x_1 + iy_1 = (x_1, y_1)` and `z_2 = x_2 + iy_2 = (x_2 , y_2),` where `x_1, y_1, x_2 , y_2 in R` and
`i = sqrt(-1)` , be two complex numbers.
If `anglePOQ = theta` , then from Coni method,

`(z_2-0)/(z_1-0) = |z_2|/|z_1| e^(i theta)`

`=> (z_2barz_1)/(z_1barz_1) = |z_2|/|z_1| e^(i theta) => (z_2barz_1)/|barz_1|^2 = |z_2|/|z_1|e^(i theta)`

`z_2barz_1 = |z_1| |z_2| e^(i theta)`

`z_2 barz_1 = |z_1| |z_2| (cos theta + i sin theta)`

`=> Re (z_2barz_1) = |z_1| |z_2|cos theta...............(i)`

and Im `(z_2barz_1)= |z_1||z_2| sin theta .............(ii)`

The dot product `z_1` and `z_2` is defined by,
`z_1·z_2 = | z_1|| z_2 | cos theta` `= Re (barz_1 z_2 ) = x_1x_2 + y_1y_2` [from Eq. (i)]
and cross product of `z_1` and `z_2` is defined by `z_1 xx z_2 =| z_1 || z_2| sin theta`

`= Im (barz_1z_2) = x_1y_z - x_zy_1` [from Eq. (ii)]

Hence, `z_1·z_2 = x_1x_2 + y_1y_2 = Re(barz_1z_2)` and `z_1 x z2 = x_1y_2 - x_2 y_1 = Im (barz_1z_2)`

`text(Fundas)`

1. If `z_1` and `z_2` are perpendicular, then `z_1 · z_2 = 0`
2. If `z_1` and `z_2` are parallel, then `z_1 xx z_2 = 0`
3. Projection of `z_1` on `z_2 = (z_1·z_2) /| z_2|`
4. Projection of `z_2` on `z_1 = (z_1·z_2)/|z_1 |`
5. Area of triangle, if two sides represented by `z_1` and `z_2` is `1/2 | z_1 xx z_2 |`.
6. Area of a parallelogram having sides `z_1` and `z_2` is `| z_1 xx z_2 |` .
7. Area of parallelogram, if diagonals represented by `z_1` and `z_2` is `1/2 | z_1 xx z_2 |`.