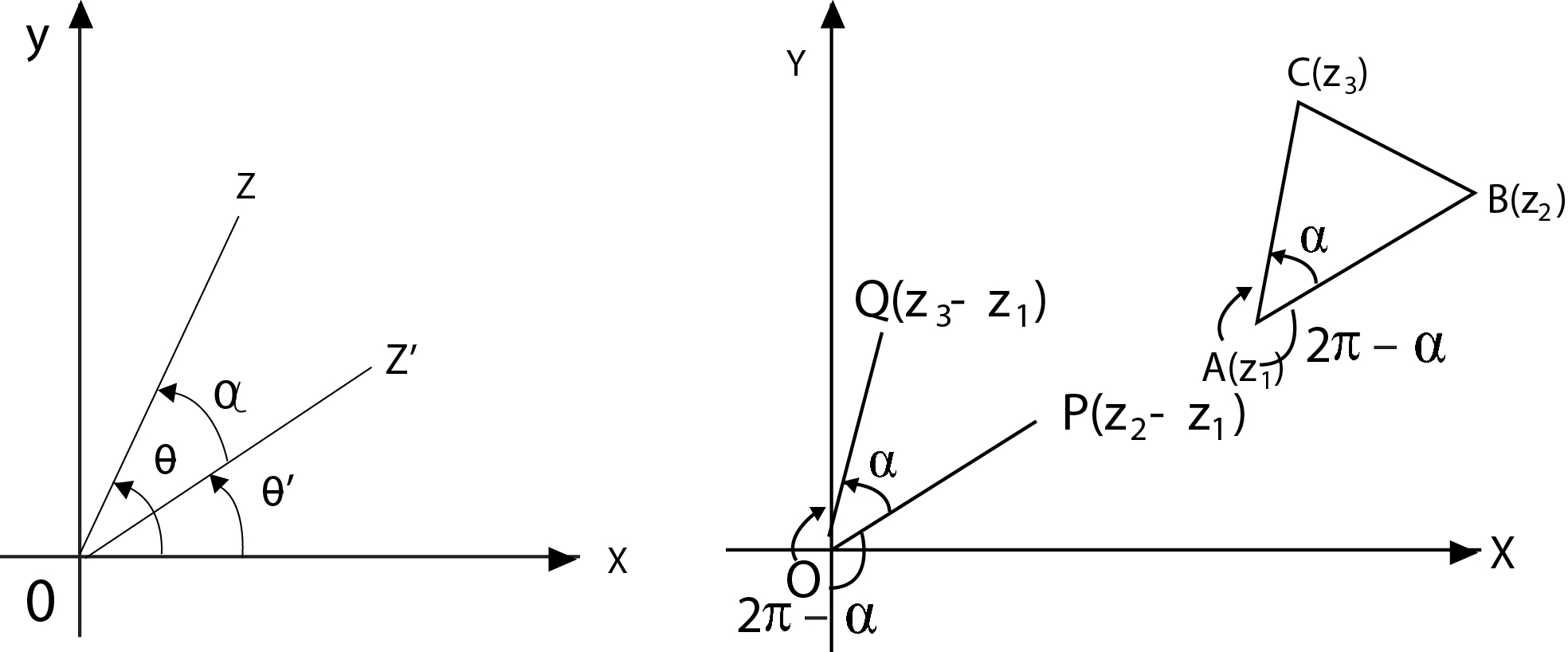
If `z` and `z'` are two complex numbers then argument of `z/(z')` is the angle through which `Oz'` must be turned in order that it may lie along `Oz` .

`z/(z')=(|z|e^(i theta))/(|z'| e^(i theta'))=(|z|)/(|z'|)e^(i(theta-theta'))=(|z|)/(|z'|)e^(i alpha)`

In general, let `z_1,z_2, z_3` be the three vertices of a triangle `ABC` described in the counter-clock wise sense. Draw `OP` and `OQ` parallel and equal to `AB` and `AC` respectively. Then the point `P` is `z_2 - z_1` and `Q` is `z_3 - z_1` and

`(z_3-z_1)/(z_2-z_1)=(OQ)/(OP) (cos alpha+i sin alpha)`

`(CA)/(BA) . e^(i alpha)=(|z_3-z_1|)/(|z_2-z_1|) . e^(i alpha)`

Note that arg. `(z_3 - z_1) - arg(z_2 - z_1) = a` is the angle through which ` OP` must be rotated in the anti-clockwise direction so that it conciders with `OQ` .

Here we can write `(|z_3-z_1|)/(z_2-z_1)=(|z_3-z_1|)/(|z_2-z_1|) . e^(-i(2 pi-alpha))` also. ln case we are rotating `OP` in clockwise direction by an angle `(2 pi - alpha)`. Since the rotation is in clockwise direction, we are taking negative sign with angle
`(2 pi - alpha)`.


``
`text(Note : )`

`1.` Here, only principal values of the arguments are considered.
`2.` `arg((z_1-z_2)/(z_3-z_4)) = theta `, if AB considers. with CD, then `arg((z_1-z_2)/(z_3-z_14)) =0` or `pi` , so that `((z_1-z_2)/(z_3-z_4))` is real . It follows that if `((z_1-z_2)/(z_3-z_4))` is real . then the points A,B,C,D are collinear .
`3.` If AB is perpendicular to CD, then
`arg((z_1-z_2)/(z_3-z_4)) + pm pi/2 ,` so `((z_1-z_2)/(z_3-z_4))` is purely imaginary.
`4.` It follows that, if `z_1 - z_2 = pm k (z_3 - z_4)` , where k is purely imaginary number,
then AB and CD are perpendicular to each other.