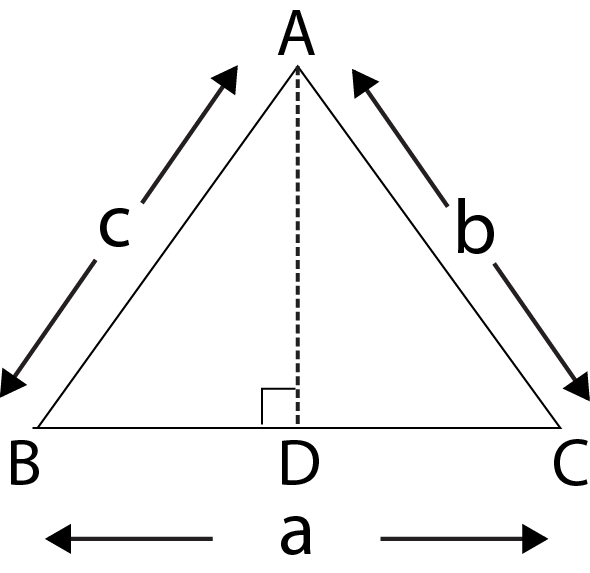
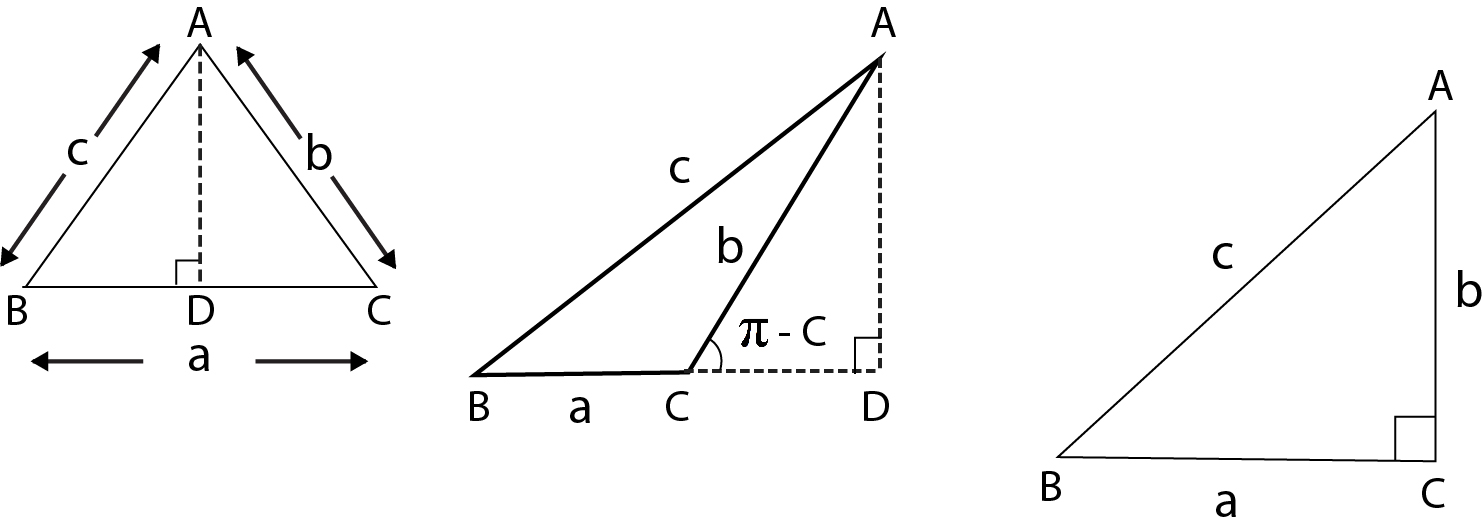
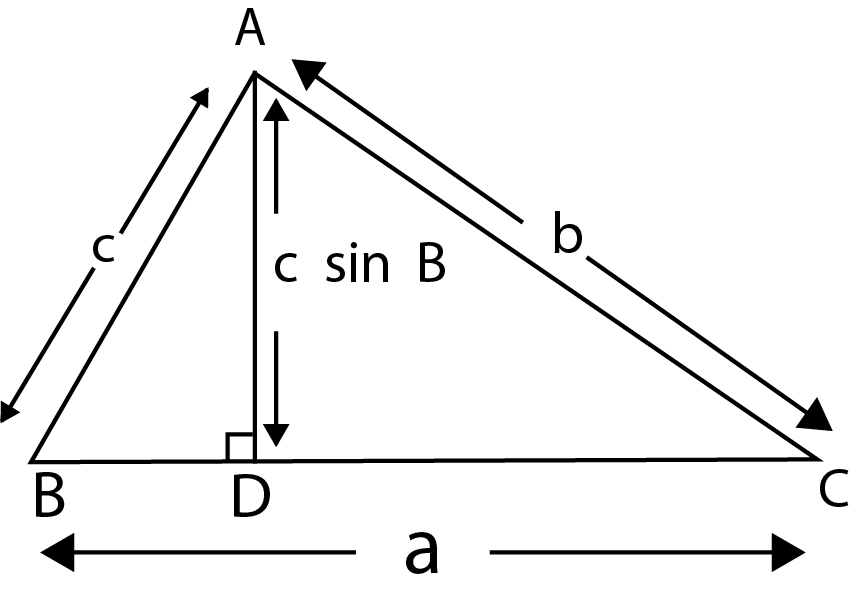
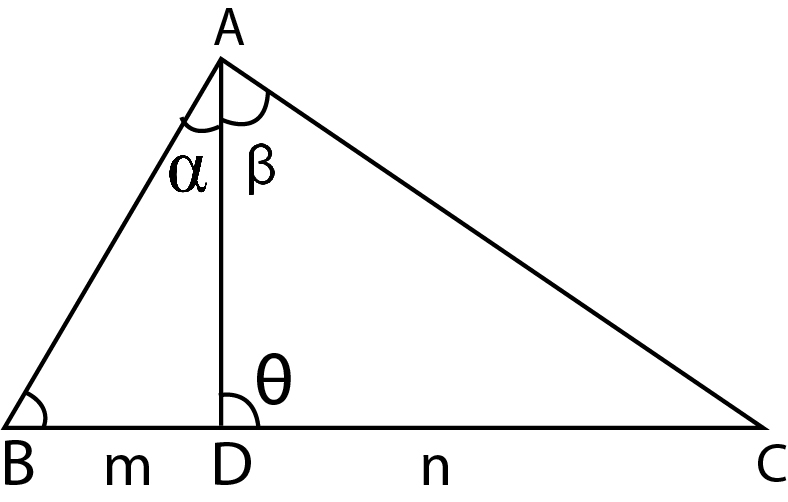
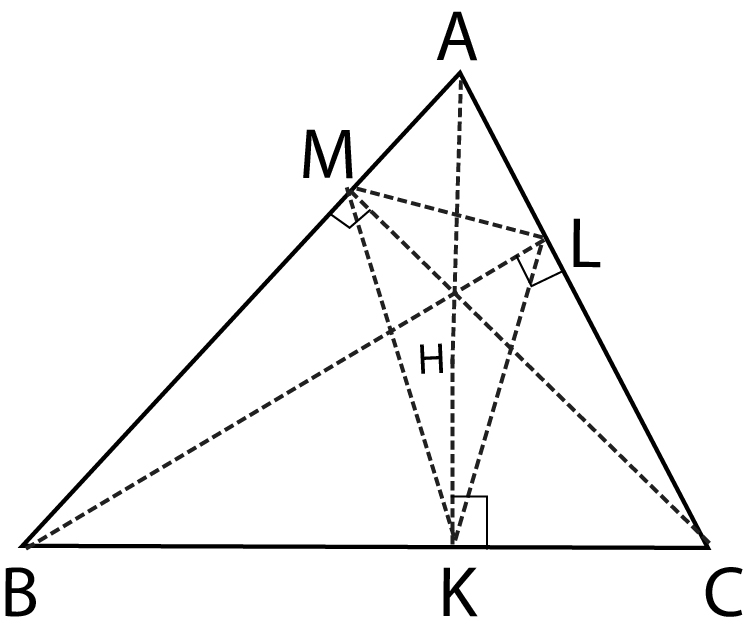
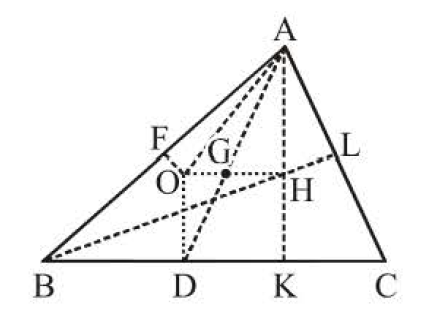
Let `ABC` be any triangle and let `AK, BL` and `CM` to be perpendiculars from `A, B` and `C` upon the opposite sides of the triangle. It can be easily shown from geometry, that these three perpendiculars meet in a common point `H`. This point `H` is called the orthocentre of the triangle. The triangle `KLM`, which is formed by joining the feet of these perpendicular, is called the pedal triangle of `ABC`.
Distances of the orthocentre of the angular points of the triangle :
Consider an acute angle triangle `ABC`.
We have, `HK = KB tan (HBK) = KB tan (90^(circ) - C) = KB cot C`
`= AB cos B cot C =AB cos B (cosC/sin C) =AB/ sin C cos B cos C`
`HK= c/ sin C cos B cos C = 2R cos B cos C`
Agaiin, `AH = AL sec (KAC)= c cos A sec (90^(circ) -C)`
`= c cos A cosec C =c / sin C cos A = 2R cos A`
similarly `BH =2R cos B `and `CH = 2R cos C`.
The distances of the orthocentre from the angular point are therefore, `2R cos A, 2R cos B` and
`2R cos C`. Its distance from the sides `a, b, c` are `2R cos B cos C, 2R cos C cos A and 2R cos A cos B`
respectively.
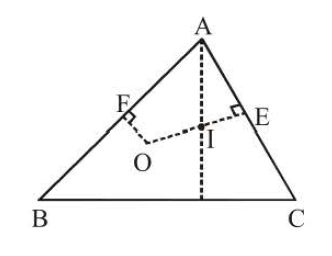
The sides and angles to the pedal triangle :
Consider an acute angle triangle `ABC`:
Since the angles `HKC` and `H LC` are right angles, the points `H, L, C` and `K` lie on a circle.
`angle HKL = angle HCL = 90^(circ) - A` Similarly.
`H, K, B, M` lie on a circle, and therefore,
`angle HKM = angle HBM= 90^(circ) - A`
Hence `angle MKL = 180^(circ) - 2A = the supplement of 2A`.
` angle KLM =180^(circ) - 28, angle LMK = 180^(circ) - 2C`.
Again, from the triangle `ALM`, we have
`(LM)/ sin A= (AL)/ (sin (AML))=( AB cos A)/(cos (HML))= (c cos A)/(cos (HAL)) = (c cos A)/(sin C)`
`LM= c /(sin C ) cos A sin A =c/(sin C) sin A cos A= a cos A`
so, `LM = a cos A`, similarly `MK = b cos B, KL = c cos C`
The sides of the pedal triangle therefore `a cos A, b cos Band c cos C`; also its angles are the supplements
of twice the angles of the triangle.
Let `ABC` be any triangle and let `AK, BL` and `CM` to be perpendiculars from `A, B` and `C` upon the opposite sides of the triangle. It can be easily shown from geometry, that these three perpendiculars meet in a common point `H`. This point `H` is called the orthocentre of the triangle. The triangle `KLM`, which is formed by joining the feet of these perpendicular, is called the pedal triangle of `ABC`.
Distances of the orthocentre of the angular points of the triangle :
Consider an acute angle triangle `ABC`.
We have, `HK = KB tan (HBK) = KB tan (90^(circ) - C) = KB cot C`
`= AB cos B cot C =AB cos B (cosC/sin C) =AB/ sin C cos B cos C`
`HK= c/ sin C cos B cos C = 2R cos B cos C`
Agaiin, `AH = AL sec (KAC)= c cos A sec (90^(circ) -C)`
`= c cos A cosec C =c / sin C cos A = 2R cos A`
similarly `BH =2R cos B `and `CH = 2R cos C`.
The distances of the orthocentre from the angular point are therefore, `2R cos A, 2R cos B` and
`2R cos C`. Its distance from the sides `a, b, c` are `2R cos B cos C, 2R cos C cos A and 2R cos A cos B`
respectively.
The sides and angles to the pedal triangle :
Consider an acute angle triangle `ABC`:
Since the angles `HKC` and `H LC` are right angles, the points `H, L, C` and `K` lie on a circle.
`angle HKL = angle HCL = 90^(circ) - A` Similarly.
`H, K, B, M` lie on a circle, and therefore,
`angle HKM = angle HBM= 90^(circ) - A`
Hence `angle MKL = 180^(circ) - 2A = the supplement of 2A`.
` angle KLM =180^(circ) - 28, angle LMK = 180^(circ) - 2C`.
Again, from the triangle `ALM`, we have
`(LM)/ sin A= (AL)/ (sin (AML))=( AB cos A)/(cos (HML))= (c cos A)/(cos (HAL)) = (c cos A)/(sin C)`
`LM= c /(sin C ) cos A sin A =c/(sin C) sin A cos A= a cos A`
so, `LM = a cos A`, similarly `MK = b cos B, KL = c cos C`
The sides of the pedal triangle therefore `a cos A, b cos Band c cos C`; also its angles are the supplements
of twice the angles of the triangle.