Property -1 :
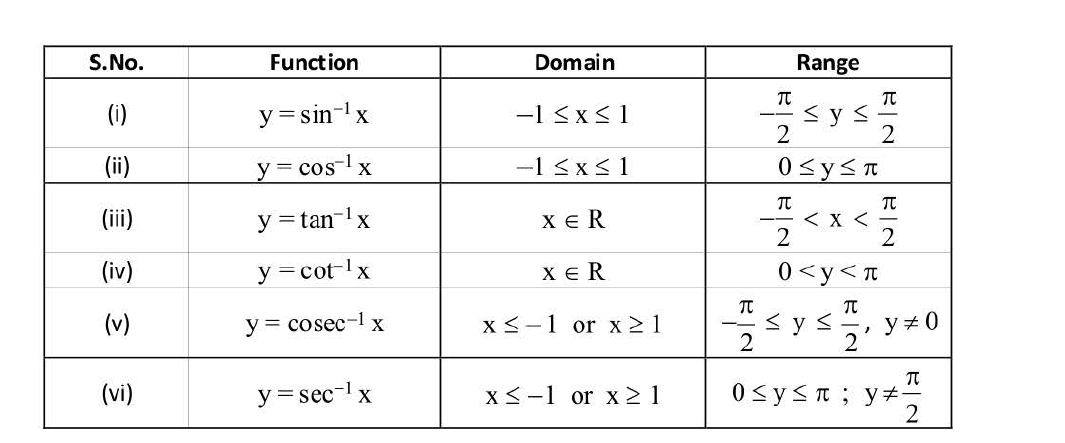
(i) `sin (sin^- 1 x) = x , - 1 le x le 1` (ii) `cos(cos^-1 x)=x , - 1 le x le1`
(iii) `tan (tan^- 1 x) = x , x in R` (iv) `cot (cot^-1 x) = x , x in R`
(v) `cosec(cosec^- 1 x) = x , |x | ge 1` (vi) `sec (sec^- 1 x) = x , | x | ge 1`
Property-2 :
( 1 ) `cosec^-1x = sin^-1 1/x ; |x| ge 1`
(2) `sin^-1x = cosec^-1 1/x , |x| le 1, x ne 0`
(3) `sec^-1 x = cos^-1 1/x ; |x| ge 1`
(4) `cos^-1 x = sec^-1 1/x , |x| le 1, x ne 0`
(5) `cot^-1x = tan^-1 1/x ; x >0`
`= pi+ tan ^-1 1/x ; x < 0`
Note:
(i) `cosec^-1x` and `sin^-1 1/x` are identical function.
(ii) `sin^-1 x` and `cosec^-1 1/x` are not identical because domain of `sin^-1 x` and `cosec^-1 1/x` is not equal.
(iii) `sec^-1x` and `cos^-1 1/x` are identical function.
(iv) `cos^-1 x` and `sec^-1 1/x` are not identical because domain of `cos^-1 x ` and `sec^-1 1/x` is not equal.
Property-3 :
(i) `sin^-1 (- x) = - sin^-1x , - 1 le x le 1`
(ii) `tan^- 1 (- x) = - tan^- 1 x , x in R`
(iii) `cos^- 1 (- x) = pi - cos^- 1 x , - 1 le x le 1`
(iv) `cot^-1 (- x) = pi - cot^-1 x , x in R`
(v) `cosec^-1 (- x) = - cosec^- 1 x , | x | ge 1`
(vi) `sec^- 1 (- x) = pi - sec^- 1 x, | x | ge 1`
Property-4 :
(i) `sin^- 1 x + cos^- 1 x= pi/2, - 1 le x le 1` (ii) `tan^-1 x + cot^-1 x = pi/2 , x in R`
(iii) `cosec^- 1 x + sec^- 1 x = pi/2 , |x| ge1`
Property-5 :
(1) `tan^-1 x + tan^-1 y` `= {tt( ( tan^-1((x+y)/(1-xy) ) , text(if) xy < 1) ,(pi+tan^-1((x+y)/(1-xy) ) , text(if) x > 0, y>0 text(and) xy > 1) ,(-pi+ tan^-1 ((x+y)/(1-xy))) )`
Proof:
Let `tan^-1x= A` and `tan^-1 y= B` , where `A,B in ( -pi/2, pi/2)`.
Now, `tan(A+B) = (tanA+tanB)/(1-tanAtanB) =(x+y)/(1-xy)`
`=> tan^-1 ((x+y)/(1-xy)) = tan^-1 tan (A+B)`
`= tan^-1 tan alpha ` where `alpha in (-pi, pi)`
`tan^-1 ((x+y)/(1-xy))= tan^-1 (tan alpha)`
`= {tt((alpha+pi, -pi < alpha < -pi/2),(alpha , -pi/2 le alpha le pi/2),(alpha-pi, pi/2 < alpha < pi) ) ={tt((tan^-1x+tan^-1y + pi, -pi < tan^-1x+tan^-1y< -pi/2),(tan^-1x+tan^-1y, -pi/2 le tan^-1x +tan^-1y le pi/2),(tan^-1x+tan^-1y -pi, pi/2 < tan^-1 x +tan^-1y < pi)) `
Case-I :
`- pi < tan^-1 x+tan^-1 y pi/2 ` `=> x < 0 , y < 0`
Also , `tan^-1 x < -pi/2 - tan^-1 y`
`=> tan^-1 x < - (pi/2 -tan^-1 (-y))` `=> x < -(-1/y) => x < 1/y => xy>1`
Case-ll:
`pi/2 < tan^-1 x +tan^-1 y < pi => x,y >0`
Also, `tan^-1x > pi/2 -tan^-1 y => tan^-1x > tan^(-1) 1/y=>x > 1/y => xy >1`
Case-Ill :
`-pi/2 le tan^-1 x +tan^-1 y le pi/2 => xy <1`
(2) `x > 0` and `y > 0, tan^-1 x - tan^- 1y = tan^-1 (x-y)/(1+xy)` (with no other restriction)
`x > 0` and `y > 0, tan^-1 x - tan^- 1y = tan^-1 (x-y)/(1+xy)` (with no other restriction)
(Remember)
(i) `tan^(-1) 1 + tan^(-1) 2 + tan^(-1)3 = pi`
(ii) `tan^(-1)1 +tan^(-1) 1/2+tan^(-1) 1/3 =pi/2`
(iii) ` (tan^(-1)1 +tan^(-1)2+tan^(-1)3) /(cot^(-1 ) 1 +cot^(-1) 2+cot^(-1) 3)=2`
Sol .(i) `tan^(-1 ) 1 +tan^(-1) 2+tan^(-1)3 = tan^(-1) + (pi+tan^-1 ((2+3)/(1-2*3)))`
`=tan^(-1) 1 + (pi +tan^(-1) (-1))`
`pi/4 +pi - pi/4 =pi`
(ii) `tan^(-1) 1 +tan^(-1) (1/2) +tan^(-1) 1 +tan^-1 ((1/2+1/3)/(1-1/2*1/3)) `
`= tan^(-1) 1 + tan^-1 (5/5)= tan^(-1 ) 1 +tan^(-1) 1= pi/4+pi/4=pi/2`
(iii) `(tan^(-1) 1 +tan^(-1) 2+ tan^(-1) 3)/(cot^(-1) 1 +cot^(1-) 2 + cot^(-1) 3) = (tan^(-1)1 +tan^(-1)2 +tan^(-1)3)/(tan^(-1) 1 + tan^(-1) 1/2+tan^(-1) 1/3)= (pi)/(pi/2) =2`
Property-6 :
(I) `sin^(-1) x +sin^(-1) y` `= [tt( (sin^(-1) (root x (1-y^2)+root y (1-x^2)) text(if) x ge 0; y ge 0 text(and) x^2 +y^2 le 1) , (pi-sin^(-1) (root x (1-y^2)+ root y (1-x^2) ) text(if) x ge 0; y ge 0 text(and) x^2+y^2 >1))`
note that `x^2 + y^2 le 1` `=> 0 ge sin^(- 1)x + sin^(-1)y le pi/2`
Let `sin^(-1) x= alpha` and `sin^(-1) y = beta `; `alpha beta in [0,pi/2]`
now `x^2+y^2 le 1`
`sin^2alpha+sin^2beta le 1` `=> sin^2alpha .e cos^2beta`
`sin^2 alpha le sin^2 (pi/2 -beta) => alpha le pi/2 - beta => alpha+beta le pi/2`
`0 le sin^(-1) x + sin^(-1) y le pi/2 ]`
and `x^2+y^2 >1 => pi/2 < sin^(-1) x+sin^(-1) y < pi`
This formula should normally be used in establishing the identities.
e.g. find whether `sin^(-1) (3/5) +sin^(-1) (12/5) `it becomes simple.
(II)
we have `sin^(-1) x -sin^(-1)y=sin^(-1) (root x (1-y^2) -root y (1-x^2)) ,x > 0; y > 0`
and `cos^(-1) x pm cos^(-1) y =cos^(-1) (xy pm sqrt (1-x^2) sqrt (1-y^2)),x> 0 ,y >0, x < y`
Property -7 :
`tan^(-1)x + tan^(-1)y + tan^(-1)z = tan^(-1) [ (x+y+z -xyz)/(1- (xy+yz+zx))]`
where `x > 0, y > 0, z > 0` Solution and `xy + yz + zx < 1` and `xy < 1 , yz < 1 , zx < 1`
Solution
`tan^(-1)x + tan^(- 1)y + tan^(-1)z = tan^(-1) ((x+y)/(1-xy))+ tan^(-1) z`
`= tan^(-1) ((((x+y)/(1-xy))+z)/(1-((x+y)/(1-xy))z)) = tan^(-1) (x+y+z-xyz)/(1-xy-(x+y)z)= tan^(-1) (x+y+z-xyz)/(1- (xy +yz +zx))`
Property -1 :
(i) `sin (sin^- 1 x) = x , - 1 le x le 1` (ii) `cos(cos^-1 x)=x , - 1 le x le1`
(iii) `tan (tan^- 1 x) = x , x in R` (iv) `cot (cot^-1 x) = x , x in R`
(v) `cosec(cosec^- 1 x) = x , |x | ge 1` (vi) `sec (sec^- 1 x) = x , | x | ge 1`
Property-2 :
( 1 ) `cosec^-1x = sin^-1 1/x ; |x| ge 1`
(2) `sin^-1x = cosec^-1 1/x , |x| le 1, x ne 0`
(3) `sec^-1 x = cos^-1 1/x ; |x| ge 1`
(4) `cos^-1 x = sec^-1 1/x , |x| le 1, x ne 0`
(5) `cot^-1x = tan^-1 1/x ; x >0`
`= pi+ tan ^-1 1/x ; x < 0`
Note:
(i) `cosec^-1x` and `sin^-1 1/x` are identical function.
(ii) `sin^-1 x` and `cosec^-1 1/x` are not identical because domain of `sin^-1 x` and `cosec^-1 1/x` is not equal.
(iii) `sec^-1x` and `cos^-1 1/x` are identical function.
(iv) `cos^-1 x` and `sec^-1 1/x` are not identical because domain of `cos^-1 x ` and `sec^-1 1/x` is not equal.
Property-3 :
(i) `sin^-1 (- x) = - sin^-1x , - 1 le x le 1`
(ii) `tan^- 1 (- x) = - tan^- 1 x , x in R`
(iii) `cos^- 1 (- x) = pi - cos^- 1 x , - 1 le x le 1`
(iv) `cot^-1 (- x) = pi - cot^-1 x , x in R`
(v) `cosec^-1 (- x) = - cosec^- 1 x , | x | ge 1`
(vi) `sec^- 1 (- x) = pi - sec^- 1 x, | x | ge 1`
Property-4 :
(i) `sin^- 1 x + cos^- 1 x= pi/2, - 1 le x le 1` (ii) `tan^-1 x + cot^-1 x = pi/2 , x in R`
(iii) `cosec^- 1 x + sec^- 1 x = pi/2 , |x| ge1`
Property-5 :
(1) `tan^-1 x + tan^-1 y` `= {tt( ( tan^-1((x+y)/(1-xy) ) , text(if) xy < 1) ,(pi+tan^-1((x+y)/(1-xy) ) , text(if) x > 0, y>0 text(and) xy > 1) ,(-pi+ tan^-1 ((x+y)/(1-xy))) )`
Proof:
Let `tan^-1x= A` and `tan^-1 y= B` , where `A,B in ( -pi/2, pi/2)`.
Now, `tan(A+B) = (tanA+tanB)/(1-tanAtanB) =(x+y)/(1-xy)`
`=> tan^-1 ((x+y)/(1-xy)) = tan^-1 tan (A+B)`
`= tan^-1 tan alpha ` where `alpha in (-pi, pi)`
`tan^-1 ((x+y)/(1-xy))= tan^-1 (tan alpha)`
`= {tt((alpha+pi, -pi < alpha < -pi/2),(alpha , -pi/2 le alpha le pi/2),(alpha-pi, pi/2 < alpha < pi) ) ={tt((tan^-1x+tan^-1y + pi, -pi < tan^-1x+tan^-1y< -pi/2),(tan^-1x+tan^-1y, -pi/2 le tan^-1x +tan^-1y le pi/2),(tan^-1x+tan^-1y -pi, pi/2 < tan^-1 x +tan^-1y < pi)) `
Case-I :
`- pi < tan^-1 x+tan^-1 y pi/2 ` `=> x < 0 , y < 0`
Also , `tan^-1 x < -pi/2 - tan^-1 y`
`=> tan^-1 x < - (pi/2 -tan^-1 (-y))` `=> x < -(-1/y) => x < 1/y => xy>1`
Case-ll:
`pi/2 < tan^-1 x +tan^-1 y < pi => x,y >0`
Also, `tan^-1x > pi/2 -tan^-1 y => tan^-1x > tan^(-1) 1/y=>x > 1/y => xy >1`
Case-Ill :
`-pi/2 le tan^-1 x +tan^-1 y le pi/2 => xy <1`
(2) `x > 0` and `y > 0, tan^-1 x - tan^- 1y = tan^-1 (x-y)/(1+xy)` (with no other restriction)
`x > 0` and `y > 0, tan^-1 x - tan^- 1y = tan^-1 (x-y)/(1+xy)` (with no other restriction)
(Remember)
(i) `tan^(-1) 1 + tan^(-1) 2 + tan^(-1)3 = pi`
(ii) `tan^(-1)1 +tan^(-1) 1/2+tan^(-1) 1/3 =pi/2`
(iii) ` (tan^(-1)1 +tan^(-1)2+tan^(-1)3) /(cot^(-1 ) 1 +cot^(-1) 2+cot^(-1) 3)=2`
Sol .(i) `tan^(-1 ) 1 +tan^(-1) 2+tan^(-1)3 = tan^(-1) + (pi+tan^-1 ((2+3)/(1-2*3)))`
`=tan^(-1) 1 + (pi +tan^(-1) (-1))`
`pi/4 +pi - pi/4 =pi`
(ii) `tan^(-1) 1 +tan^(-1) (1/2) +tan^(-1) 1 +tan^-1 ((1/2+1/3)/(1-1/2*1/3)) `
`= tan^(-1) 1 + tan^-1 (5/5)= tan^(-1 ) 1 +tan^(-1) 1= pi/4+pi/4=pi/2`
(iii) `(tan^(-1) 1 +tan^(-1) 2+ tan^(-1) 3)/(cot^(-1) 1 +cot^(1-) 2 + cot^(-1) 3) = (tan^(-1)1 +tan^(-1)2 +tan^(-1)3)/(tan^(-1) 1 + tan^(-1) 1/2+tan^(-1) 1/3)= (pi)/(pi/2) =2`
Property-6 :
(I) `sin^(-1) x +sin^(-1) y` `= [tt( (sin^(-1) (root x (1-y^2)+root y (1-x^2)) text(if) x ge 0; y ge 0 text(and) x^2 +y^2 le 1) , (pi-sin^(-1) (root x (1-y^2)+ root y (1-x^2) ) text(if) x ge 0; y ge 0 text(and) x^2+y^2 >1))`
note that `x^2 + y^2 le 1` `=> 0 ge sin^(- 1)x + sin^(-1)y le pi/2`
Let `sin^(-1) x= alpha` and `sin^(-1) y = beta `; `alpha beta in [0,pi/2]`
now `x^2+y^2 le 1`
`sin^2alpha+sin^2beta le 1` `=> sin^2alpha .e cos^2beta`
`sin^2 alpha le sin^2 (pi/2 -beta) => alpha le pi/2 - beta => alpha+beta le pi/2`
`0 le sin^(-1) x + sin^(-1) y le pi/2 ]`
and `x^2+y^2 >1 => pi/2 < sin^(-1) x+sin^(-1) y < pi`
This formula should normally be used in establishing the identities.
e.g. find whether `sin^(-1) (3/5) +sin^(-1) (12/5) `it becomes simple.
(II)
we have `sin^(-1) x -sin^(-1)y=sin^(-1) (root x (1-y^2) -root y (1-x^2)) ,x > 0; y > 0`
and `cos^(-1) x pm cos^(-1) y =cos^(-1) (xy pm sqrt (1-x^2) sqrt (1-y^2)),x> 0 ,y >0, x < y`
Property -7 :
`tan^(-1)x + tan^(-1)y + tan^(-1)z = tan^(-1) [ (x+y+z -xyz)/(1- (xy+yz+zx))]`
where `x > 0, y > 0, z > 0` Solution and `xy + yz + zx < 1` and `xy < 1 , yz < 1 , zx < 1`
Solution
`tan^(-1)x + tan^(- 1)y + tan^(-1)z = tan^(-1) ((x+y)/(1-xy))+ tan^(-1) z`
`= tan^(-1) ((((x+y)/(1-xy))+z)/(1-((x+y)/(1-xy))z)) = tan^(-1) (x+y+z-xyz)/(1-xy-(x+y)z)= tan^(-1) (x+y+z-xyz)/(1- (xy +yz +zx))`