Simplest way to define integration is as an antiderivative the inverse of a derivative. Derivative of `sin x` is
`cos x` then we may say that integral of `cos x` is `sin x`.
In general , if we consider

`d/dx f(x) =phi (x)`

or, using differentials `d f(x) = phi (x) dx`;
then an integral of `phi(x)` with respect to `x` or an integral of `phi (x) dx` is `f(x)` and symbolically, we write,
`int phi (x) dx = f(x)`


where the symbol `int` which is an elongated `S` (the first letter of the word sum, or, of the Latin word
Swnma) is known as the sign of integration. Now we come to some forma l definitions:

The actual process of finding the function, when its derivative or its differential is known, is called Integration
as anti-derivative; the function to which the integration is applied is called Integrand and the function
obtained as a result of integration is said to be lntegral. In the above case, `phi (x)` is the integrand and `f(x)`
is the integral.

The process of integrating many ordinary functions is simple, but in general, integration is more involved
than differentiation, as will be evident from future discussions.

Summary:
If `d/dx [F(x) +C]= f(x) ` then `F(x) +C` is called an antiderivative of `f(x)` on `[a, b]` and is written as

`int f(x) dx =F(x) +C`
In this case we say that the function `f(x)` is integrable on `[a, b]`. Note that every function is not integrable.

e.g. `f(x) = [tt( (0,text(if) x in Q) ,(1, text(if) x notin Q) )` is not integrable in `[0, 1]`. Every function which is continuous on a closed and bounded interval is integrable.

However for integrability function `f(x)` may only be piece wise continuous in `(a, b)`

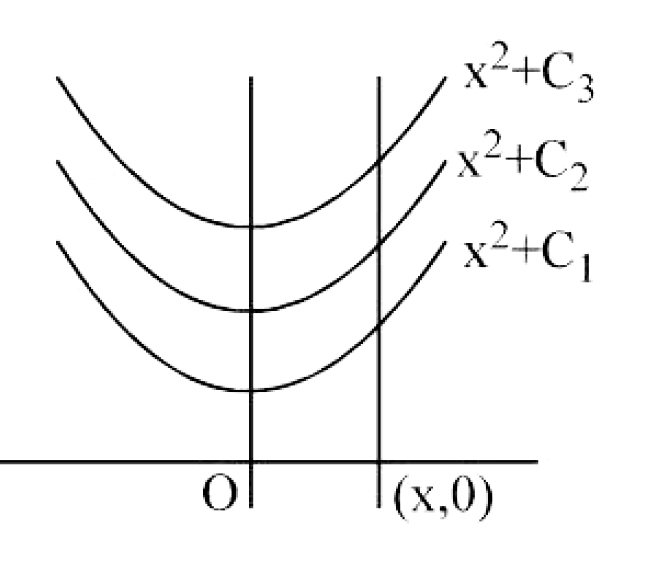
(I) Geometrical interpretation :
`y = int 2x dx =x^2/2 +C`
`y = int f(x) dx =F(x) =C`

`=> F' (x) =f(x) ; F'(x_1) =f(x_1)`
Hence `y= int f(x) ` denotes a family of curves such that the slope of the tangent at
`x = x_1` one very member is same. i.e. `F'(x_1)=f (x) ` (when `x_1` 1ies in the domain of `f(x))`
hence anti detivative of a function is not unique. If `g_1 (x)` and `g_2(x)` are two antidetivatives of a function
`f(x)` on `[a, b]` then they differ only by a constant i.e. `g_1(x) - g_2(x) = C`


(2) Antiderivative of a continuous function is differentiable

i.e. If `f(x)` is continuous then `int f(x) dx =F(x) +C=> F'(x) =f(x) =>F' (x)` is always exists

`=> F (x)` is differentiable


(3) If integrand is discontinuous at `x = x_1` then its antiderivative at `x = x_1` need not be discontinuous.
i.e. e.g. `int x^(-1/3)dx ` here `x^(-1/3)` is discontinuous at `x = 0`.

but `int x^(-1/3)dx=3/2 x^(2/3) +C` is continuous at `x = 0`

(4) If `d/dx (F(x) +C) = f(x) => int f(x) dx =F(x)+C` then only we say that `f(x)` is integrable.

(5) Anti derivative of a periodic function need not be a periodic function

e.g. `f(x) = cos x +1` is periodic but `int ( cos x+1)dx = sin x+x +C` is aperiodic.

Some times it is possible to convert given integral as a loving integral (Standrad integral) after simple
manipulation.

Often it is not possible to convert an integral into loving integral just by simple manipulation. Then required
some techniques to convert an integral into loving integral. This techniques are following.

SUBSTITUTION :

Theory : `I= int f(x) dx ` and let `x = phi (z)`

`dI/dx =f(x)`; `dx/dz = phi ' (z)`

`=> dI/dz = (dI/dx )*dx/dz = f(x) * phi ' (z)` or `dI/dz = f (phi (z)) phi'(z)`

Hence `I= int f (phi (z)) phi' (z) dz` ....................(1)

Substitution is said to be appropriate if the integrand in (I) is a loving one (standard integral)
If `int [f(x)]^n f' (x) dx ` or `int f'(x) /[f(x)]^n dx`

start with `f(x) =t`

`int (tan x)dx = ln sec x+C = -lm(cos x) +C`;
`int (cot x)dx =ln (sin x)` (loving integrals)

Proof: `int tan xdx = int sinx/cosx dx`
put `cos x =t` to get `int -dt/t= -ln t+c = -ln (cos x)+c =ln (sec x)+c`