Product Of Vectors: SCALAR OR DOT PRODUCT
Product of two vectors is done by two methods when the product of two vectors results in a scalar quantity then it is called `text(scalar product.)` It is also called as `text(dot product)` because this product is represented by putting a `text(dot.)`
When the product of two vectors results in a vector quantity then this product is called `text(Vector Product.)` This product is represented by `(x)` sign so that it is also called as `text(cross product.)`
`text(Scalar or dot product of two vectors :)`
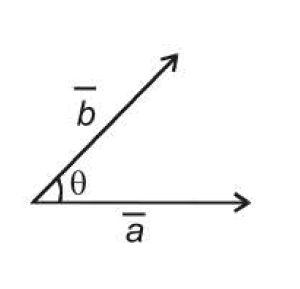
`text(Definition:)` If `vec(a)` and `vec(b)` are two vectors and `theta` be the angle between their tails or heads, then their scalar product (or dot product) is defined as the number `| vec(a)| |vec(b) | cos theta`
where `|vec(a)|` and `|vec(b)|` are modulii of `vec(a)` and `vec(b)` respectively and `0 le theta le pi` . It is denoted by `vec(a)*vec(b)` . Thus
`quadquadquadquadquadquadvec(a)*vec(b) = | vec(a) | *|vec(b) | cos theta`
`text(Note:)`
`(i)` `vec(a)*vec(b) in R`
`(ii)` `vec(a)*vec(b) le |vec(a)| |vec(b)|`
`(iii)` `quadquadvec(a)*vec(b) >0 =>` angle between `a` and `vec(b)` say `theta in [0,pi/2 )`
`quadquadquadquadvec(a)*vec(b) < 0 =>` angle between `vec(a)` and `vec(b)` say `theta in (pi/2 , pi]`
`quadquadquadquadvec(a)*vec(b) =0 =>` angle between `vec(a)` and `vec(b)` say `theta = pi/2` or atleast one of `vec(a)` and `vec(b)` is zero vector.
`(iv)` The dot product of a zero and non- zero vector is a scalar zero i.e. `vec(0)*vec(a)=0`.
`(v)` If `theta` be angle between any two non zero vector `vec(a) & vec(b)` then `cos theta = (vec(a)*vec(b))/( |vec(a) | *|vec(b)| )`
`text(Scalar product in particular cases : )`
`1.` `vec(a)*vec(b) =vec(b)*vec(a)`
`2.` `vec(a) * (vec(b)+vec(c)) =vec(a)*vec(b)+vec(a)*vec(c)`
`3.` `(m vec(a))*vec(b)= m (vec(a)*vec(b)) = vec(a) *(m vec(b))`
`4.` If `theta =0 => vec(a)*vec(b)= |vec(a)| |vec(b)|` (like vectors)
`5.` If `theta =pi => vec(a)*vec(b)=- |vec(a)| |vec(b)|` (unlike vectors)
`6.` If `hat(a)` and `hat(b)` are unit vectors then `hat(a)*hat(b)= cos theta` (where `theta` is angle between them).
`7.` `vec(a)*vec(a) = |vec(a)|^2 => |vec(a)| =sqrt (vec(a)*vec(a))`
`8.` If `vec(a) bot vec(b) => vec(a)*vec(b) =0` but `vec(a)*vec(b) =0 => vec(a)=vec(0)` or `vec(b)=vec(0)` or `vec(a) bot vec(b)`
`9.` If `hat(i),hat(j)` and `hat(k)` are unit vectors along the rectangular coordinate are `OX, OY` and `OZ` then
`quadquadquadquadquadhat(i)*hat(i) =hat(j)*hat(j)=hat(k)*hat(k) =1 , quadquadquadhat(i)*hat(j) =hat(j)*hat(k)=hat(k)*hat(i)=0`
`10.` `vec(a)*vec(b) =vec(a)*vec(c)` does not implies `vec(b) =vec(c)`
Infact `vec(a)*vec(b) =vec(a)*vec(c) => vec(a) * (vec(b)-vec(c))=0 => vec(a)=0` or `vec(b) =vec(c)` or `vec(a) bot (vec(b)-vec(c))`
`11.` `(vec(a)*vec(b))* vec(c)` is meaningless
`text(Note : )`` (a) ` `(vec(a)*vec(b))*vec(b)` is not defined `quadquad(b)` `(vec(a)+vec(b))^2= |vec(a)|^2+2 vec(a)*vec(b) + |vec(b)|^2`
`quadquad (c)` `(vec(a)-vec(b))^2=| vec(a)|^2-2 vec(a)*vec(b) + |vec(b)|^2``quadquad (d) ``(vec(a)+vec(b))* (vec(a)- vec(b))= |vec(a)|^2-|vec(b)|^2`
`quadquadquadquad (e)` `|vec(a)+vec(b) | =|vec(a)|+|vec(b)| => vec(a) | |vec(b)` `quadquad(f)` ` |vec(a)+vec(b) |^2 = |vec(a)|^2+|vec(b)|^2 => vec(a) bot vec(b)`
`quadquadquadquad(g)` ` |vec(a)+vec(b) | = |vec(a)-vec(b) | = vec(a) bot vec(b)`
`text(Scalar product in terms of components : )`
Let `vec(a)` and `vec(b)` be two vectors such that `vec(a) =a_1 hat(i)+a_2 hat(j)+a_3 hat(k)` and `vec(b) =b_1 hat(i) +b_2 hat(j) +b_3 hat(k)`
Then `vec(a)*vec(b) = a_1b_1 +a_2b_2 +a_3b_3`
In particular
`vec(a)*vec(a) = |vec(a)|^2 =a_1^2 +a_2^2 +a_3^2`
For any vector `vec(a)` ,
`vec(a) = (vec(a)*hat(i) )hat(i) + (vec(a)*hat(j) )hat(j) + (vec(a)*hat(k) )hat(k)`
When the product of two vectors results in a vector quantity then this product is called `text(Vector Product.)` This product is represented by `(x)` sign so that it is also called as `text(cross product.)`
`text(Scalar or dot product of two vectors :)`
`text(Definition:)` If `vec(a)` and `vec(b)` are two vectors and `theta` be the angle between their tails or heads, then their scalar product (or dot product) is defined as the number `| vec(a)| |vec(b) | cos theta`
where `|vec(a)|` and `|vec(b)|` are modulii of `vec(a)` and `vec(b)` respectively and `0 le theta le pi` . It is denoted by `vec(a)*vec(b)` . Thus
`quadquadquadquadquadquadvec(a)*vec(b) = | vec(a) | *|vec(b) | cos theta`
`text(Note:)`
`(i)` `vec(a)*vec(b) in R`
`(ii)` `vec(a)*vec(b) le |vec(a)| |vec(b)|`
`(iii)` `quadquadvec(a)*vec(b) >0 =>` angle between `a` and `vec(b)` say `theta in [0,pi/2 )`
`quadquadquadquadvec(a)*vec(b) < 0 =>` angle between `vec(a)` and `vec(b)` say `theta in (pi/2 , pi]`
`quadquadquadquadvec(a)*vec(b) =0 =>` angle between `vec(a)` and `vec(b)` say `theta = pi/2` or atleast one of `vec(a)` and `vec(b)` is zero vector.
`(iv)` The dot product of a zero and non- zero vector is a scalar zero i.e. `vec(0)*vec(a)=0`.
`(v)` If `theta` be angle between any two non zero vector `vec(a) & vec(b)` then `cos theta = (vec(a)*vec(b))/( |vec(a) | *|vec(b)| )`
`text(Scalar product in particular cases : )`
`1.` `vec(a)*vec(b) =vec(b)*vec(a)`
`2.` `vec(a) * (vec(b)+vec(c)) =vec(a)*vec(b)+vec(a)*vec(c)`
`3.` `(m vec(a))*vec(b)= m (vec(a)*vec(b)) = vec(a) *(m vec(b))`
`4.` If `theta =0 => vec(a)*vec(b)= |vec(a)| |vec(b)|` (like vectors)
`5.` If `theta =pi => vec(a)*vec(b)=- |vec(a)| |vec(b)|` (unlike vectors)
`6.` If `hat(a)` and `hat(b)` are unit vectors then `hat(a)*hat(b)= cos theta` (where `theta` is angle between them).
`7.` `vec(a)*vec(a) = |vec(a)|^2 => |vec(a)| =sqrt (vec(a)*vec(a))`
`8.` If `vec(a) bot vec(b) => vec(a)*vec(b) =0` but `vec(a)*vec(b) =0 => vec(a)=vec(0)` or `vec(b)=vec(0)` or `vec(a) bot vec(b)`
`9.` If `hat(i),hat(j)` and `hat(k)` are unit vectors along the rectangular coordinate are `OX, OY` and `OZ` then
`quadquadquadquadquadhat(i)*hat(i) =hat(j)*hat(j)=hat(k)*hat(k) =1 , quadquadquadhat(i)*hat(j) =hat(j)*hat(k)=hat(k)*hat(i)=0`
`10.` `vec(a)*vec(b) =vec(a)*vec(c)` does not implies `vec(b) =vec(c)`
Infact `vec(a)*vec(b) =vec(a)*vec(c) => vec(a) * (vec(b)-vec(c))=0 => vec(a)=0` or `vec(b) =vec(c)` or `vec(a) bot (vec(b)-vec(c))`
`11.` `(vec(a)*vec(b))* vec(c)` is meaningless
`text(Note : )`` (a) ` `(vec(a)*vec(b))*vec(b)` is not defined `quadquad(b)` `(vec(a)+vec(b))^2= |vec(a)|^2+2 vec(a)*vec(b) + |vec(b)|^2`
`quadquad (c)` `(vec(a)-vec(b))^2=| vec(a)|^2-2 vec(a)*vec(b) + |vec(b)|^2``quadquad (d) ``(vec(a)+vec(b))* (vec(a)- vec(b))= |vec(a)|^2-|vec(b)|^2`
`quadquadquadquad (e)` `|vec(a)+vec(b) | =|vec(a)|+|vec(b)| => vec(a) | |vec(b)` `quadquad(f)` ` |vec(a)+vec(b) |^2 = |vec(a)|^2+|vec(b)|^2 => vec(a) bot vec(b)`
`quadquadquadquad(g)` ` |vec(a)+vec(b) | = |vec(a)-vec(b) | = vec(a) bot vec(b)`
`text(Scalar product in terms of components : )`
Let `vec(a)` and `vec(b)` be two vectors such that `vec(a) =a_1 hat(i)+a_2 hat(j)+a_3 hat(k)` and `vec(b) =b_1 hat(i) +b_2 hat(j) +b_3 hat(k)`
Then `vec(a)*vec(b) = a_1b_1 +a_2b_2 +a_3b_3`
In particular
`vec(a)*vec(a) = |vec(a)|^2 =a_1^2 +a_2^2 +a_3^2`
For any vector `vec(a)` ,
`vec(a) = (vec(a)*hat(i) )hat(i) + (vec(a)*hat(j) )hat(j) + (vec(a)*hat(k) )hat(k)`