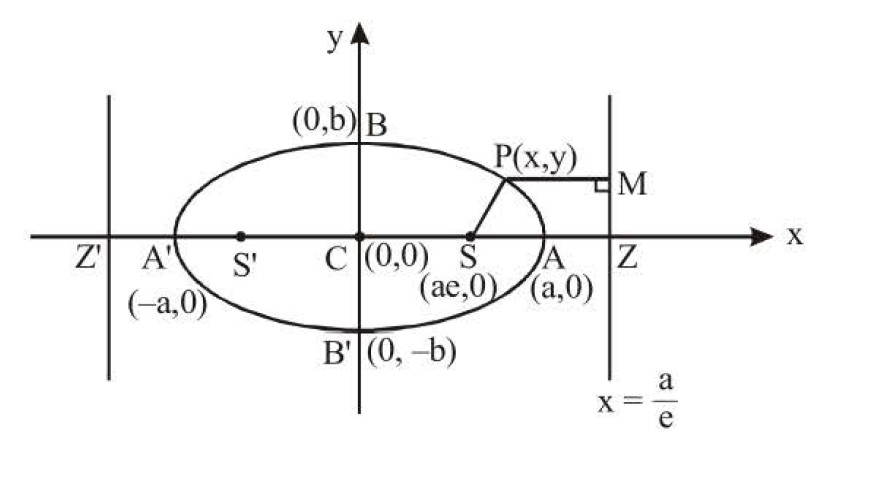
(1) By the symmetry of equation of ellipse, if we take second focus `S'( - ae, 0)` & second directrix `x =- a/e` & perform same calculation, we get same equation of ellipse, therefore there are two focii & two directrix of an ellipse. The two focii of ellipse are `(ae, 0)` and (- ae, 0) and the two corresponding directrices are lines `x = -a/e` and `x =- a/e` . If focus of the ellipse is taken as `(ae, 0)`, then corresponding directrix is `x=-a/e` and if focus is `(- ae, 0)`, then corresponding directrix is `x = -a/e`
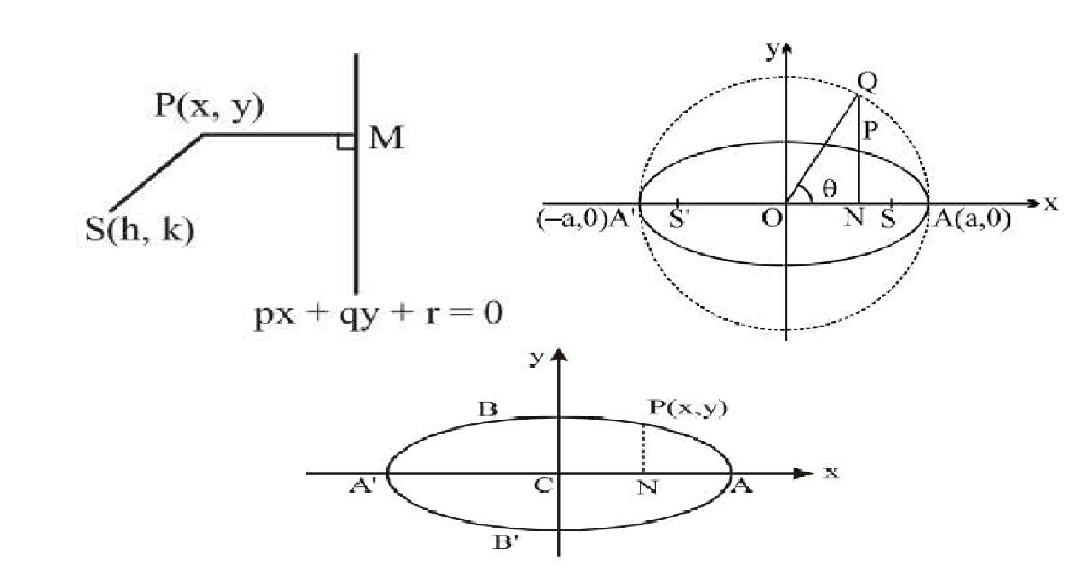
(2) If equation of directrix is `px + qy+ r= 0` & focus is `(h, k)` then its equation will be
`PS^2 = e^2 PM^2`
`(x-h)^2+(y-k)^2=e^2.((px+qy+r)/(sqrt(p^2+q^2)))^2`
(3) Distance between foci `SS' = 2ae` & distance between directrix `Z Z' = 2 a/e`
(4) Degree of flatness of an ellipse is also called on eccentricity & written as
`e=(CS)/(CA)=(text(Distance from centre to focus))/(text(Distance from centre to vertex))`
If `e -> 0 => b -> a =>` foci becomes closer & move towards centre and ellipse becomes circle.
If `e-> 1 =>b-> 0 =>` ellipse get thinner & thinner
(5) Two ellipse are said to be similar if they have same eccentricity.
(6) Distance of focus from the extremity of minor axis is equal to `'a'` because `a^2e^2 + b^2 = a^2`
(7) Let `P(x, y)` be any point on the ellipse .
`x^2/a^2+y^2/b^2=1`
`:. y^2/b^2=1-x^2/a^2`
`=> y^2/b^2=(((a-x)(a+x))/a^2) => (PN^2)/b^2= (AN . A' N)/a^2`
`=> (PN^2)/(AN .A'N) =b^2/a^2`
(1) By the symmetry of equation of ellipse, if we take second focus `S'( - ae, 0)` & second directrix `x =- a/e` & perform same calculation, we get same equation of ellipse, therefore there are two focii & two directrix of an ellipse. The two focii of ellipse are `(ae, 0)` and (- ae, 0) and the two corresponding directrices are lines `x = -a/e` and `x =- a/e` . If focus of the ellipse is taken as `(ae, 0)`, then corresponding directrix is `x=-a/e` and if focus is `(- ae, 0)`, then corresponding directrix is `x = -a/e`
(2) If equation of directrix is `px + qy+ r= 0` & focus is `(h, k)` then its equation will be
`PS^2 = e^2 PM^2`
`(x-h)^2+(y-k)^2=e^2.((px+qy+r)/(sqrt(p^2+q^2)))^2`
(3) Distance between foci `SS' = 2ae` & distance between directrix `Z Z' = 2 a/e`
(4) Degree of flatness of an ellipse is also called on eccentricity & written as
`e=(CS)/(CA)=(text(Distance from centre to focus))/(text(Distance from centre to vertex))`
If `e -> 0 => b -> a =>` foci becomes closer & move towards centre and ellipse becomes circle.
If `e-> 1 =>b-> 0 =>` ellipse get thinner & thinner
(5) Two ellipse are said to be similar if they have same eccentricity.
(6) Distance of focus from the extremity of minor axis is equal to `'a'` because `a^2e^2 + b^2 = a^2`
(7) Let `P(x, y)` be any point on the ellipse .
`x^2/a^2+y^2/b^2=1`
`:. y^2/b^2=1-x^2/a^2`
`=> y^2/b^2=(((a-x)(a+x))/a^2) => (PN^2)/b^2= (AN . A' N)/a^2`
`=> (PN^2)/(AN .A'N) =b^2/a^2`