Vector equation of bisectors of angle between two straight lines :
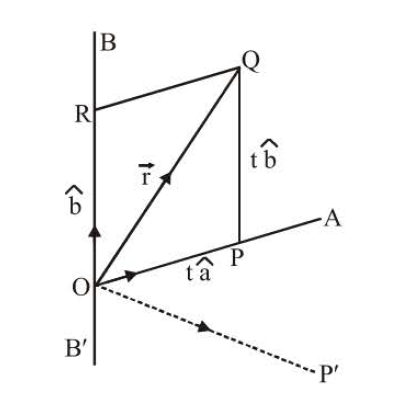
Let `OA` and `OB` be the given straight line parallel to unit vectors `hat(a)` and `hat(b)`, respectively. Take the point
`O` as origin, and Jet `Q` be a point on the internal bisector of the angle `AOB`. From `Q` draw `QR` parallel to
`OA` cutting `OB` at `R`.
Now `:.` `angle AOQ = angle BOQ ` (as `OQ` is the bisector)
and `angle BOQ =angle OQp ` (alternative angles)
`:.` `angle AOQ =angle OQP` `:.` `OP=QP =t` (say), where t is a scalar.
`:.` `vec(OP) =t hat(a)` and `vec(PQ)= t hat(b)`
`vec(OQ)= vec(r)`
Let `vec(OQ)=vec(OP)+vec(PQ)`
or `vec(r)= t hat(a)+ t hat(a)`
` vec(r) = t ( hat(a) +hat(b))`
or, ` vec(a) =t ( (vec(a)/a)+(vec(b)/a) )`
where ` | vec(a)| =a , |vec(b)| =b`
This is the equation of internal bisector of `angle AOB`
`O` as origin, and Jet `Q` be a point on the internal bisector of the angle `AOB`. From `Q` draw `QR` parallel to
`OA` cutting `OB` at `R`.
Now `:.` `angle AOQ = angle BOQ ` (as `OQ` is the bisector)
and `angle BOQ =angle OQp ` (alternative angles)
`:.` `angle AOQ =angle OQP` `:.` `OP=QP =t` (say), where t is a scalar.
`:.` `vec(OP) =t hat(a)` and `vec(PQ)= t hat(b)`
`vec(OQ)= vec(r)`
Let `vec(OQ)=vec(OP)+vec(PQ)`
or `vec(r)= t hat(a)+ t hat(a)`
` vec(r) = t ( hat(a) +hat(b))`
or, ` vec(a) =t ( (vec(a)/a)+(vec(b)/a) )`
where ` | vec(a)| =a , |vec(b)| =b`
This is the equation of internal bisector of `angle AOB`