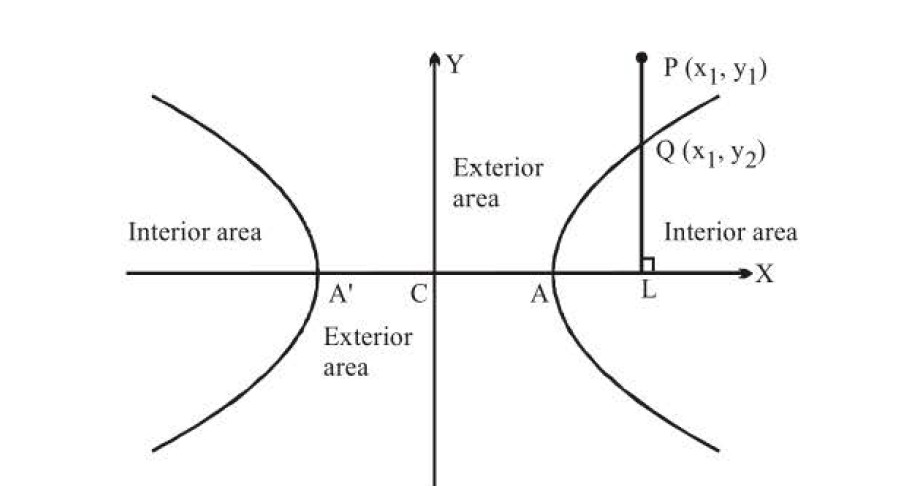
Terms Related to Hyperbola :
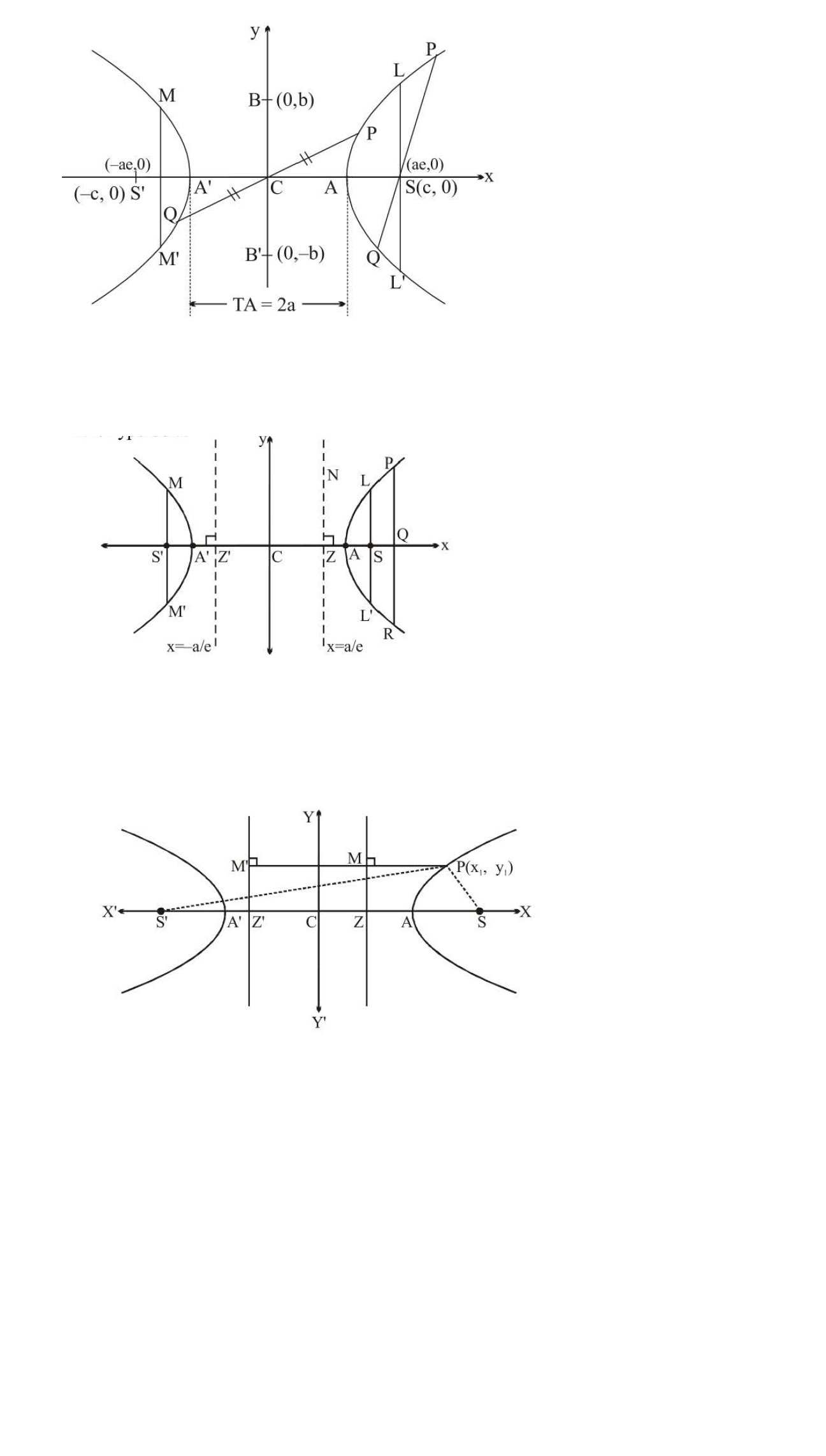
(1) Centre :
In the figure, `C` is the centre of the ellipse. All chords passing through `C` are called diameter and bisected at `C`.
(2) Foci :
`S(a e, 0)` and `S'(- a e, 0)` are two foci of hyperbola. Line containing the fixed points `S` and `S'` (called Foci) is called Transverse Axis `(TA)` or Focal Axis and the distance between `S` and `S'` is called Focal Length.
(3) Axes :
The line `A A'` is called transverse axis and the line `B B'` is perpendicular to it and passes through the centre `(0, 0)` of the hyperbola is called conjugate axis.
The length of transverse and conjugate axes are taken as `2a` and `2b` respectively.
The transverse and conjugate axes together are called principal axes of hyperbola and their intersection point is called the centre of hyperbola.
The points of intersection of the directrix with the transverse axis are known as Foot of the directrix (`Z` and `Z'` ).
(4) Vertex :
The points of intersection `(A, A')` of the curve with the transverse axis are called Vertices of the hyperbola.
(5) Double Ordiante :
Any chord perpendicular to the Transverse axis is called a Double Ordinate.
(6) Latus-Rectum :
When double ordinates passes through the focus of parabola then it is called the latus rectum. In the given figure `L L'` and `M M'` are the latus-rectums of the hyperbola.
let `L L' = 2k` then `LS = L'S = k`
Let `L(ae, k)` lie on the hyperbola `x^2/a^2-y^2/b^2=1`
`:. (a^2e^2)/a^2-k^2/b^2=1`
or `k^2=b^2(e^2-1)=b^2(b^2/a^2)` `[:. b^2=a^2(e^2-1)]`
`:. k=b^2/a`
`:. 2k=(2b^2)/a=L L'`
= `(2e)` (distance between the focus and the foot of the corresponding directrix)
End points oflatus -rectums are
`L=(ae,b^2/a), L'=(ae,-b^2/a); M=(-ae,b^2/a); M'=(-ae,-b^2/a)` respectively
(7) Focal Chord :
A chord of hyperbola passing through its focus is called a focal chord.
(8) Eccentricity :
For the hyperbola `x^2/a^2-y^2/b^2=1` we have
`b^2=a^3(e^2-1)`
`=> e= sqrt(1+(b^2/a^2))=> e= sqrt({1+(text(conjugate axis)^2)/(text(transverse axis)^2)})`
Eccentricity defines the curvature of the hyperbola and is mathematically spelled as:
`e = (text(distance from centre to focus))/(text(distance from centre to vertex))`
(9) Focal Distance of a Point On Hyperbola :
The hyperbola is `x^2/a^2-y^2/b^2=1` ...................(1)
The foci `S` and `S'` are `(ae, 0)` and `(- ae, 0)` & corresponded directrix are `x =a/e` and `x = -a/e` respectively.
Let `P(x_1, y_1)` be any point on `(1)`.
Now `SP = ePM = e(x_1-a/e)=ex_1-a`
and `S'P = ePM' = e(x_1+a/e)=ex_1+a`
`:. S'P - SP = (ex_1 + a) - (ex_1 - a) = 2a`
`= A A' =` Transverse axis
Thus hyperbola is the locus of a point which moves in a plane such that the difference of its distances from two
fixed point (foci) is constant and always equal to transverse axis.
Hence, in the given figure
`PS' - PS = QS' - QS = RS - RS' =` length of transverse axis.
In the figure, `C` is the centre of the ellipse. All chords passing through `C` are called diameter and bisected at `C`.
(2) Foci :
`S(a e, 0)` and `S'(- a e, 0)` are two foci of hyperbola. Line containing the fixed points `S` and `S'` (called Foci) is called Transverse Axis `(TA)` or Focal Axis and the distance between `S` and `S'` is called Focal Length.
(3) Axes :
The line `A A'` is called transverse axis and the line `B B'` is perpendicular to it and passes through the centre `(0, 0)` of the hyperbola is called conjugate axis.
The length of transverse and conjugate axes are taken as `2a` and `2b` respectively.
The transverse and conjugate axes together are called principal axes of hyperbola and their intersection point is called the centre of hyperbola.
The points of intersection of the directrix with the transverse axis are known as Foot of the directrix (`Z` and `Z'` ).
(4) Vertex :
The points of intersection `(A, A')` of the curve with the transverse axis are called Vertices of the hyperbola.
(5) Double Ordiante :
Any chord perpendicular to the Transverse axis is called a Double Ordinate.
(6) Latus-Rectum :
When double ordinates passes through the focus of parabola then it is called the latus rectum. In the given figure `L L'` and `M M'` are the latus-rectums of the hyperbola.
let `L L' = 2k` then `LS = L'S = k`
Let `L(ae, k)` lie on the hyperbola `x^2/a^2-y^2/b^2=1`
`:. (a^2e^2)/a^2-k^2/b^2=1`
or `k^2=b^2(e^2-1)=b^2(b^2/a^2)` `[:. b^2=a^2(e^2-1)]`
`:. k=b^2/a`
`:. 2k=(2b^2)/a=L L'`
= `(2e)` (distance between the focus and the foot of the corresponding directrix)
End points oflatus -rectums are
`L=(ae,b^2/a), L'=(ae,-b^2/a); M=(-ae,b^2/a); M'=(-ae,-b^2/a)` respectively
(7) Focal Chord :
A chord of hyperbola passing through its focus is called a focal chord.
(8) Eccentricity :
For the hyperbola `x^2/a^2-y^2/b^2=1` we have
`b^2=a^3(e^2-1)`
`=> e= sqrt(1+(b^2/a^2))=> e= sqrt({1+(text(conjugate axis)^2)/(text(transverse axis)^2)})`
Eccentricity defines the curvature of the hyperbola and is mathematically spelled as:
`e = (text(distance from centre to focus))/(text(distance from centre to vertex))`
(9) Focal Distance of a Point On Hyperbola :
The hyperbola is `x^2/a^2-y^2/b^2=1` ...................(1)
The foci `S` and `S'` are `(ae, 0)` and `(- ae, 0)` & corresponded directrix are `x =a/e` and `x = -a/e` respectively.
Let `P(x_1, y_1)` be any point on `(1)`.
Now `SP = ePM = e(x_1-a/e)=ex_1-a`
and `S'P = ePM' = e(x_1+a/e)=ex_1+a`
`:. S'P - SP = (ex_1 + a) - (ex_1 - a) = 2a`
`= A A' =` Transverse axis
Thus hyperbola is the locus of a point which moves in a plane such that the difference of its distances from two
fixed point (foci) is constant and always equal to transverse axis.
Hence, in the given figure
`PS' - PS = QS' - QS = RS - RS' =` length of transverse axis.