Condition for coplanarity of four points :
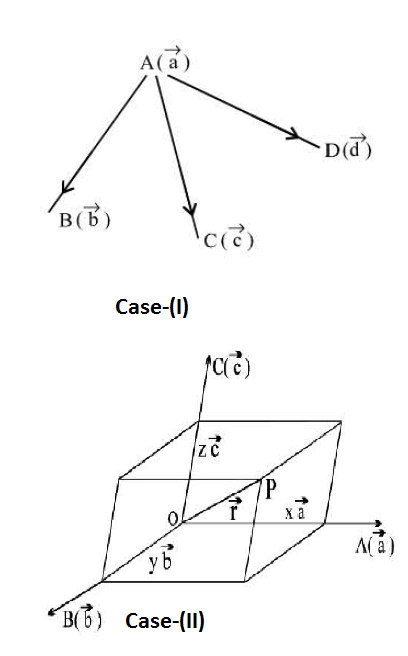
4 points with pv's `vec(a),vec(b),vec(c),vec(d)` are coplanar iff `EE` scalars x, y, z and t not all simultaneously zero and satisfying
`xvec(a) + yvec(b)+zvec(c)+ tvec(d) =0` where `x + y + z + t = 0`.
Case I :
Let the four points `A, B, C, D` are in the same plane
`=> ` the vectors `vec(b) -vec(a)` ,`vec(c) -vec(a)` and `vec(d)-vec(a)` are in the same plane.
Hence `vec(d) -vec(a)` `= l (vec(b) -vec(a)) + m (vec(c) -vec(a))`
or ` underbrace( l + m-1)_(x) vec(a) - underbrace(l)_(y) vec(b) - underbrace(m)_(z) vec(c) + underbrace(1)_(t) vec(d) =0 => x vec(a) +yvec(b) +zvec(c) +tvec(d) =0` where `x+y+z+t =0` and `x, y, z, t` not all simultaneous zero.
Case ll :
Let `xvec(a) + yvec(b) +zvec(c)+tvec(d)=0` where `x + y + z + t = 0` and not all simultaneously zero
Let `t ne 0` `(-y-z-t) vec(a) +yvec(b)+zvec(c)+tvec(d)=0` [putting `x =- y - z - t`]
` (vec(d) -vec(a))t + y (vec(b)-vec(a)) +z (vec(c)-vec(a)) =0`
`=> vec(d)-vec(a), vec(b)-vec(a)` and `vec(c)-a` are coplanar `=> ` points `A, B, C, D` are coplanar
Theorem in space :
If `vec(a),vec(b),vec(c)` are `3` non zero non coplanar vectors then any vector `vec(r)` can be
expressed as a linear combination: `vec(r) = xvec(a) + y vec(b) +zvec(c)` of `vec(a),vec(b),vec(c)`
Examples:
Express the non coplanar vectors `vec(a),vec(b),vec(c)` in terms of `vec(b)xx vec(c) , vec(c)xx vec(a) ,vec(a)xx vec(b) `
Since ` [vec(a)vec(b)vec(c)]^2 = [(vec(a) xx vec(b)) (vec(b) xx vec(c)) (vec(c) xx vec(a)) ]`
`:.` If `vec(a) ,vec(b),vec(c)` are non-coplanar
`=> vec(a) xx vec(b),vec(b) xx vec(c),vec(c) xx vec(a)` are also non coplanar.
` vec(a) = x (vec(a) xx vec(b)) + y (vec(b) xx vec(c)) +z (vec(c) xx vec(a))`
Taking dot product with `vec(a)`
`vec(a)^2 = y [vec(a)vec(b)vec(c)] => y = (vec(a))^2/[vec(a)vec(b)vec(c)]`
Taking dot product with `vec(b)`
`vec(a)*vec(b)=z [vec(b) vec(c) vec(a)] => z = (vec(a)vec(b))/[vec(a)vec(b)vec(c)]`
Similarly taking dot product with `vec(c)`
`vec(a)*vec(c)=x [vec(a) vec(b) vec(c)] => x = (vec(a)vec(c))/[vec(a)vec(b)vec(c)]`
`:.` `vec(a) = ( (vec(a)*vec(c))(vec(a)*vec(b))+(vec(a))^2(vec(b)*vec(c))+(vec(a)*vec(b))(vec(c)*vec(a)) )/[ vec(a)vec(b)vec(c)]`
`xvec(a) + yvec(b)+zvec(c)+ tvec(d) =0` where `x + y + z + t = 0`.
Case I :
Let the four points `A, B, C, D` are in the same plane
`=> ` the vectors `vec(b) -vec(a)` ,`vec(c) -vec(a)` and `vec(d)-vec(a)` are in the same plane.
Hence `vec(d) -vec(a)` `= l (vec(b) -vec(a)) + m (vec(c) -vec(a))`
or ` underbrace( l + m-1)_(x) vec(a) - underbrace(l)_(y) vec(b) - underbrace(m)_(z) vec(c) + underbrace(1)_(t) vec(d) =0 => x vec(a) +yvec(b) +zvec(c) +tvec(d) =0` where `x+y+z+t =0` and `x, y, z, t` not all simultaneous zero.
Case ll :
Let `xvec(a) + yvec(b) +zvec(c)+tvec(d)=0` where `x + y + z + t = 0` and not all simultaneously zero
Let `t ne 0` `(-y-z-t) vec(a) +yvec(b)+zvec(c)+tvec(d)=0` [putting `x =- y - z - t`]
` (vec(d) -vec(a))t + y (vec(b)-vec(a)) +z (vec(c)-vec(a)) =0`
`=> vec(d)-vec(a), vec(b)-vec(a)` and `vec(c)-a` are coplanar `=> ` points `A, B, C, D` are coplanar
Theorem in space :
If `vec(a),vec(b),vec(c)` are `3` non zero non coplanar vectors then any vector `vec(r)` can be
expressed as a linear combination: `vec(r) = xvec(a) + y vec(b) +zvec(c)` of `vec(a),vec(b),vec(c)`
Examples:
Express the non coplanar vectors `vec(a),vec(b),vec(c)` in terms of `vec(b)xx vec(c) , vec(c)xx vec(a) ,vec(a)xx vec(b) `
Since ` [vec(a)vec(b)vec(c)]^2 = [(vec(a) xx vec(b)) (vec(b) xx vec(c)) (vec(c) xx vec(a)) ]`
`:.` If `vec(a) ,vec(b),vec(c)` are non-coplanar
`=> vec(a) xx vec(b),vec(b) xx vec(c),vec(c) xx vec(a)` are also non coplanar.
` vec(a) = x (vec(a) xx vec(b)) + y (vec(b) xx vec(c)) +z (vec(c) xx vec(a))`
Taking dot product with `vec(a)`
`vec(a)^2 = y [vec(a)vec(b)vec(c)] => y = (vec(a))^2/[vec(a)vec(b)vec(c)]`
Taking dot product with `vec(b)`
`vec(a)*vec(b)=z [vec(b) vec(c) vec(a)] => z = (vec(a)vec(b))/[vec(a)vec(b)vec(c)]`
Similarly taking dot product with `vec(c)`
`vec(a)*vec(c)=x [vec(a) vec(b) vec(c)] => x = (vec(a)vec(c))/[vec(a)vec(b)vec(c)]`
`:.` `vec(a) = ( (vec(a)*vec(c))(vec(a)*vec(b))+(vec(a))^2(vec(b)*vec(c))+(vec(a)*vec(b))(vec(c)*vec(a)) )/[ vec(a)vec(b)vec(c)]`