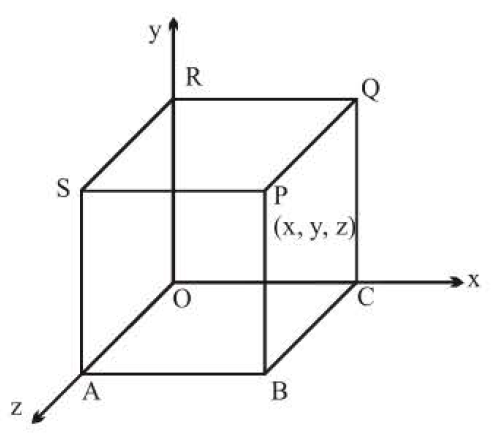
Consider a point `P` in space whose position is given by `(x, y, z)` where `x, y, z` are perpendicular
distance from `yz` plane, `zx` plane and `xy` plane respectively.

If we assume `hat(i),hat(j),hat(k)` unit vectors along `OX, OY, OZ` respectively then the position vector of point `P` is `xhat(i) +yhat(j)+zhat(k)` or simply `(x, y, z)`.

`text(When a point lies on Co-ordinates :)`

`(i)` `x` - axis `(alpha , 0, 0)`

` (ii)` `y` - axis `(0, beta, 0)`

`(iii)` `z` - axis `(0, 0, gamma)`

`(iv)` `XY` - plane `(alpha, beta , 0)`

` (v)` `XZ`- plane `(alpha , 0, gamma)`

`(vi)` `YZ`-plane `(0, beta , gamma)`