Direction ratios :
If `a, b, c` are three numbers proportional to the direction cosines `l , m, n` of a straight line, then `a, b, c` are
called its direction ratios. They are also called direction numbers or direction components.
Hence, we have ` l /a =m /b =n /c = lambda` (say) `=> l = a lambda , m = b lambda, n=c lambda `
`:.` `l^2 + m^2 +n^2 =1` `=> (a^2 +b^2 +c^2)lambda^2 =1 => lambda = pm 1/ (sqrt (a^2 +b^2 +c^2))`
`:.` `l = pm a/ (sqrt (a^2+b^2 +c^2)), m = pm b /(sqrt (a^2 +b^2 +c^2))` and `n = pm c/(sqrt (a^2 +b^2 +c^2))`
`text(Note: )`
`(i)` Direction ratios of a line is not unique but infinite in number but direction cosines will be for a line will be
only two.(`l , m, n` or `- l, - m,- n`)
`(ii)` A vector along the line with direction ratios `a, b, c` can be `ahat(i) + bhat(j) + chat(k)`.
`(iii)` Direction ratios a line joining two points `A` and `B` are proportional to `x_2 - x_1, y_2 - y_1, z_2 - z _1`.
`(iv)` `text(Projection of a Point on a Line: )`
Let `P` be a point and `AB` be a given line. Draw perpendicular `PQ` from `P` on `AB` which meets it at `Q`. This
point `Q` is called projection of `P` on the line `AB`.
`(v)` `text(Projection of a Line Segment Joining Two Points on a Line:)`
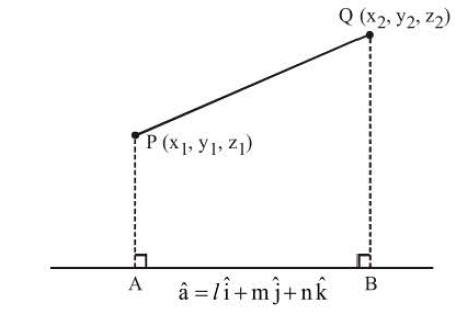
Projection of the line segment joining two points `P(x_1 y_1 z_1)` and `Q (x_2, y_2, z_2)` on another line whose
direction cosines are `l, m, n` is `AB = | l (x_2 - x_1) + m (y_2 - y_1) + n (_z2 - z_ 1) |.`
`text(Proof:)`
Vector `vecPQ = (x_2 - +x_ 1) hat(i) + (y_2 - y_1) hat(j) + (z_2 - z_1)hat(k)`
A unit vector along another line `hat (a )= l hat(i) + m hat(j) + n hat(k)` .
`:.` Projection `AB` = Projection of `vec(PQ)` on `hat (a) = |vec(PQ)* hat (a) |/|hat (a) |`
`= |l (x_2 -x_1) + m (y_2 -y_1) +n (z_2 -z_1) |`
called its direction ratios. They are also called direction numbers or direction components.
Hence, we have ` l /a =m /b =n /c = lambda` (say) `=> l = a lambda , m = b lambda, n=c lambda `
`:.` `l^2 + m^2 +n^2 =1` `=> (a^2 +b^2 +c^2)lambda^2 =1 => lambda = pm 1/ (sqrt (a^2 +b^2 +c^2))`
`:.` `l = pm a/ (sqrt (a^2+b^2 +c^2)), m = pm b /(sqrt (a^2 +b^2 +c^2))` and `n = pm c/(sqrt (a^2 +b^2 +c^2))`
`text(Note: )`
`(i)` Direction ratios of a line is not unique but infinite in number but direction cosines will be for a line will be
only two.(`l , m, n` or `- l, - m,- n`)
`(ii)` A vector along the line with direction ratios `a, b, c` can be `ahat(i) + bhat(j) + chat(k)`.
`(iii)` Direction ratios a line joining two points `A` and `B` are proportional to `x_2 - x_1, y_2 - y_1, z_2 - z _1`.
`(iv)` `text(Projection of a Point on a Line: )`
Let `P` be a point and `AB` be a given line. Draw perpendicular `PQ` from `P` on `AB` which meets it at `Q`. This
point `Q` is called projection of `P` on the line `AB`.
`(v)` `text(Projection of a Line Segment Joining Two Points on a Line:)`
Projection of the line segment joining two points `P(x_1 y_1 z_1)` and `Q (x_2, y_2, z_2)` on another line whose
direction cosines are `l, m, n` is `AB = | l (x_2 - x_1) + m (y_2 - y_1) + n (_z2 - z_ 1) |.`
`text(Proof:)`
Vector `vecPQ = (x_2 - +x_ 1) hat(i) + (y_2 - y_1) hat(j) + (z_2 - z_1)hat(k)`
A unit vector along another line `hat (a )= l hat(i) + m hat(j) + n hat(k)` .
`:.` Projection `AB` = Projection of `vec(PQ)` on `hat (a) = |vec(PQ)* hat (a) |/|hat (a) |`
`= |l (x_2 -x_1) + m (y_2 -y_1) +n (z_2 -z_1) |`