Mathematics EQUATION OF A LINE AND A PLANE IN DIFFERENT FORMS

Straight Lines :

`(A)``text(Symmetric Form : )`

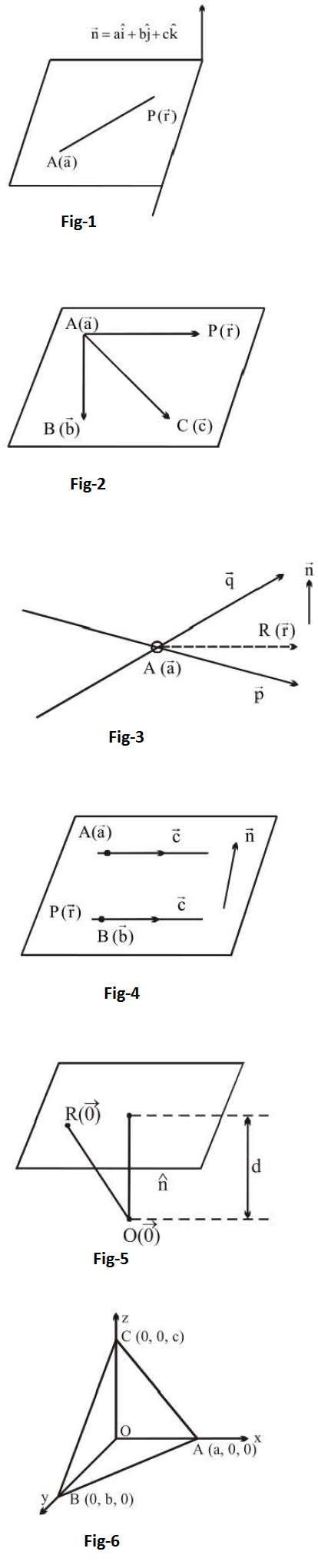
` 1 .` Equation of a straight line passing through `(x_1, y_1, z_1)` and having drs as `a, b, c` is

` (x-x_1) /a = (y-y_1)/b=(z-z_1)/c =lambda`

`text( Proof:)`

A vector parallel to line will be `ahat(i) +b hat(j) +chat(k)`.

A vector along the line can be written as

`vec(AP)=(x-x_1)hat(i)+(y-y_1)hat(j)+(z-z_1)hat(k)`

`:.` vector `vec(AP)` is parallel to `ahat(i) +b hat(j) +chat(k)`

`:.` `(x-x_1) /a = (y-y_1)/b=(z-z_1)/c =lambda`

`=>`Any point on this line can be taken as `(x_1 + lambda a, y_1 + lambda b , z_1 + lambda c)`.

`=>` lf dcs of line be `l, m, n` then its equation will `(x-x_1) /l = (y-y_1)/m=(z-z_1)/n =lambda` and any point on this line can be taken as `(x_1 + lambda a, y_1 + lambda b, z_1 + lambda c)`.

`2.` Equation of straight line passing through two points `(x_1, y_1, z_1)` and `(x_2, y_2, z_2)` will be

`(x-x_1) /(x_2 -x_1) = (y-y_1)/(y_2-y_1)=(z-z_1)/(z_2 -z_1) =lambda`

`text( Note: )`
` (i) quadquadquad (a)` Equatwno `x`-axis is`x/1=y/0=z/0` (or) `y=z=0`

`quadquadquad (b)` Equatwno `y`-axis is`x/0=y/1=z/0` (or) `x=z=0`

`quadquadquad (c)` Equatwno `z`-axis is`x/0=y/0=z/1` (or) `x=y=0`

Here zero in denominator represents that line is perpendicular to that axis.

` (ii) ` Line `(x-2)/3 = (y+1)/-2` and `z=2` is written as `(x-2)/3 = (y+1)/-2=(z-2)/0`

This line is perpendicular to `z`-axis or parallel to `xy` plane at a distance of `2` units.

`(B)``text(Unsymmetrical form of straight line :)`

The equations `a_1x + b_1y + c_1z + d_1 = 0` and `a_2x + b_2y + c_2z + d_2 = 0` together represents a line in
unsymmetrical form. This represent equation ofline of intersection of planes `a _1x + b_1y+ c_1z + d_1 = O` and
`a_2x + b_2y + c_2z + d_2 = 0`.

`(C)``text(Procedure to convert Unsymmetrical Form of straight line to Symmetrical Form :)`

Let the direction ratios of the line of intersection `(AB)` of two planes

` a_1x + b_1y +c_1z + d_1 = 0` ..... (1) and `a_2x + b_2y + c_2z +d_2 = 0`.....(2) are `a, b, c`
Direction ratios of normal to plane `(1)` are `a_1, b_1 , c_1` and
Direction ratios of normal to plane `(2)` are `a_2 , b_2 , c_2`

Line `AB` lies in both the planes `( 1)` and `(2)`
hence normals to `(1)` and `(2)` are perpendicular to `AB`.

Hence `aa_1 + b b_1 + c c_1 = 0` and `aa_2 + b b_2 + c c_2 = 0`
these two will give the proportional values of `a, b, c`.

Let the line `AB` cuts the `xy` plane at `(x_1, y_1, 0)`

Hence `a_1x_1+b_1y_1 =-d_1` and `a_2x_1+b_2y_2=-d_2` This will give a point on the line `AB`

`:.` equation of AB is `(x-x_1) /a = (y-y_1)/b=(z-z_1)/c `

Planes :

`text(Definition:)`
A plane is a surface such that a line joining any two points on the surface lies completely on it.

`text(General equation of plane :)`

A linear equation in three variables of the type `ax+ by+ cz + d = 0` represents the general equation
of a plane.
where `a, b, c` are not simultaneously zero.
Dividing by `d` we get ` (a/d)x + (b/d)y + (c/d)z +1=0`

Thus equation of plane involves only three arbitrary constants. Hence in order to determine a unique
plane 3 independent conditions are needed.

`text(Note:)`
`(i)` Equation of `xy` plane is `z = 0`.
`(ii)` Equation of `yz` plane is `x = 0`.
`(iii)` Equation of `zx` plane is `y= 0`.

`text(Division by Coordinate Planes :)`

The ratios in which the line segment `PQ` joining `P(x_ 1,y_1, z_1)` and `Q(x_2, y_2, z_2)` is divided by coordinate
planes are as follows.

`(i)` by `yz` -plane : `- x_1/x_2` ratio
`(ii)` by `zx` -plane : `- y_1/y_2` ratio
`(iii)` by `xy` -plane : `- z_1/z_2` ratio

`text(Different Forms Of The Equations of Planes : )`

`text(1 . A point in the plane and a vector normal to it is given : )`

Let a point `A( veca)` lies in the plane and a vector normal to it is `vec (n) = ahat(i)+b hat(j)+chat(k)`

`P (vec r)` is a moving point whose locus is plane then for every position of vector `vec (AP)`,
vector `vec(n)` wi ll be perpendicular to it.

`:.` `vec (AP) * vec (n) =0`

`=> (vec(r) -vec(a))*vec(n) =0` `=> vec(r)*vec(n)=vec(a)*vec(n)`

`=> vec(r)*vec(n)=d ` is general equation of plane in vector form.

It is also known as equation of plane in dot (or scalar) product form.

If `vec(r) =xhat(i) + yhat(j) +z hat(k) ` and `vec(a) =x_0hat(i) +y_0 hat(j) +z_0 hat(k) ` the equation of p lane wi ll be

`a (x- x_0) + b (y -y_0) + c (z-z_0) = 0`.

This is equation of plane containing point `(x_0, y_0, z_0)` and perpendicular to vector `vec(a) hat(i) + vec(b) hat(j) + vec(c) hat(k)`

`text(Note : )`

If equation of a plane is `ax + by + cz + d = 0` then `a, b, c` are direction ratio of normal to the plane.

`text(2. Plane passing through three given points : )`

Let three points `A (vec a), B ( vec b)` and `C (vec c)` lies in the plane and point `P (vec r)` is moving point whose locus is plane.

`:.` `vec (AP),vec (AB)` and `vec (AC)` are coplanar.

`:.` ` [ vec(r) -vec(a) vec(b) -vec(a) vec(c)-vec(a) ] =0`

In represents equation of plane passing through three points.
If `A = (x _1, y_1, z_1) , B = (x_2, y_2, z_2) , C = (x_ 3, y_3, z_3)` and `P (x, y, z)` then equation of plane is

` | (x-x_1 , y-y_1 ,z-z_1 ) ,(x_2-x_1 ,y_2-y_1 , z_2-z_1), (x_3-x_1 , y_3-y_1 ,z_3-z_1) | =0`

`text(3 . Plane containing two intersecting lines : )`

Let the equations of two lines are `vec(r) =vec(a) +lambdavec(b)` and `vec(r) =vec(a)+ muvec(b)`
Now, `n = vec(p) xxvec(q)` is a vector perpendicular to the plane.
Hence equation of plane is ` (vec(r)-vec(a)) * (vec(p) xx vec(q)) =0`

`=> [(vec(r) -vec(a) , vec(p) vec(q)) ] =0 => [ (vec(r), vec(p), vec(q)) ] => [ ( vec(a),vec(p),vec(q) ) ]`
Since vectors `vec(r) -vec(a) ,vec(p),vec(q)` are coplanar.

Therefore `vec(r) -vec(a) =lambdavec(p)+ muvec(q) => vec(r) =vec(a) +lambda vec(p) +muvec(q)`

It represents equation of a plane containing point `vec(a)` and parallel to two non-collinear vectors `vec(p)` and `vec(q)` .
This is also known as parametric equation.

`text(4 . Equation of plane containing two parallel lines :)`

Let lines be `vec(r) =vec(a) + lambdavec(b)` and `vec(r)=vec(c)+ muvec(b)`
vector normal to plane is
`vec(n) = (vec(a)-vec(c))xxvec(b)`

`:.` equation of plane is

`(vec(r) -vec(a))*(vec(a)-vec(c)) xx vec(b) =0`

`text(Alternatively : )`

Vectors `vec(r) -vec(a) , vec(c) -vec(a) ` and `vec(b)` are coplanar.

`:.` equation of plane is
`[ vec(r)-vec(a) vec(c)-vec(a) vec(b) ] =0`

`text(5. Normal form of the plane : )`

A unit vector `vec(n)` normal to the plane from origin is known and
perpendicular distance of the plane from the origin is `d`.

Projection of `vec(r)` on `vec(n) =d`

`=> vec(r)*vec(n) =d` ............(1)

`text(Note : )` `d > 0` , as `d` is distance of the plane from origin. Cartesian form of the plane is
`lx + my + nz = d`

where `I, m, n` are `dcs` of normal to plane.

`text(6 . Intercept form the plane : )`

Equation of plane in the intercept form is `x/a+y/b+z/c =1`

where `a= x`-intercept,
`b = y`-intercept, ,
`c = z`-intercept

`text(Proof: )`

Equation of plane passing through three points `A (a, 0, 0), B (0, b, 0)` and `C (0, 0, c)` will be

` | (x-a, y-0 , z-0) ,(-a,b,0) ,(-a,0 ,c) |=0`

`=> (x - a) bc - y (- ac - 0) + z (0 + ab) = 0`

`=> xbc + yac + zab = abc`

`=> x/a +y/b+z/c =1`

`text(Note :)` Area of `DeltaABC= 1/2 |vec(AB) xx vec(BC) |=1/2 | (bhat(j) -ahat(i))xx( c hat(k) -bhat(j)) | =1/2 | bchat(i) +achat(j)+abhat(k) |`

`=1/2 sqrt (a^2b^2 +b^2c^2 +c^2a^2) = sqrt ( ((ab)/2)^2 + ((bc)/2)^2 + ((ca)/2)^2 )`

`:.` Area of `Delta ABC = sqrt ( (area of Delta OAB)^2 + (area of DeltaOBC)^2 +(area of Delta OCA)^2 )`