Perpendicular Distance Of a Point From a Plane :
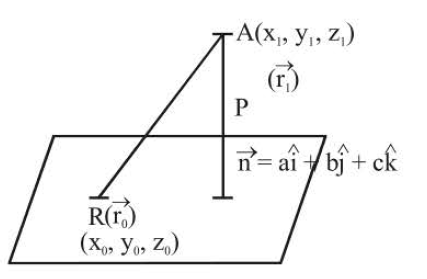
Let equation of plane is `vec(r)*vec(n)=d` then perpendicular distance from the point `A(vec (r_1)) ` on the plane = projection of `vec(RA)` on `vec(n)`.
`=> p = |( vec(r_1) -vec(r_0))*vec(n) | / | vec(n)| =| vec(r_1) * vec(n) - vec(r_0) *vec(n) |/ |vec(n) | `
`=> p = |vec(r_1)* vec(n) -vec(d) | /| vec(n)|`
If equation of plane is `ax + by+ cz+ d =0` then perpendicular distance from point `(x_1, y_1, z_1)` is given by
` |ax_1 +by_1 +cz_1 +d |/ sqrt (a^2+b^2+c^2)`
`text(Note: )`
`(i)` Planes `a_1x + b_1y + c_1z + d_1 = 0` and `a_2x + b_2y + c_2z + d =0` are
`quadquadquad (a)` parallel but not identical if ` a_1/a_2 =b_1/b_2 =c_1/c_2 ne d_1/d_2`
`quadquadquad (b)` perpendicular if `a_1a_2 +b_1b_2+c_1c_2 =0`
`quadquadquad (c)` identical if `a_1/a_2=b_1/b_2 =c_1/c_2 =d_1/d_2`
`(ii)` The equation of a plane parallel to the plane `ax + by+ cz +d` is `ax+ by + cz + k = 0`, where `k` is an arbitrary constant and is determined by the given condition.
`(iii)` Distance between two parallel planes `ax + by+ cz + d_1 = 0` and `ax+ by + cz + d_2 = 0` is equal to
` |d_1-d_2 | /sqrt (a^2+b^2+c^2)`
`(iv)` `3` planes `a_rx + b_ry + c_rz = d_r` `r 1, 2, 3`
`quadquadquad (a)` Can intersect at a point`=` system of equations in `3` variables having unique solution.
`quadquadquad (b)` Can intersect coaxially`=` system of equations in `3` variables having infinite solutions.
`quadquadquad (c)` May not have a common point `=` system of equations in `3` variables having no solution.
e.g. To illustrate our approach for finding the distance between a point and a plane, we work through an example.
Find the distance from the point `P=(4,−4,3)` to the plane `2x−2y+5z+8=0` which is pictured in the below figure in its original view.
Solution: We use the second formula from the page on distance from a point to a plane. From the equation for the plane we substitute `A=2, B=−2,C=5,D=8.` From the point PP, we substitute `x_1=4, y_1,` and `z_1=3.` The distance from PP to the plane is
`d = |2⋅4+(−2)⋅(−4)+5⋅3+8|/sqrt(2^2+(−2)^2+5^2)= 6.8`
`=> p = |( vec(r_1) -vec(r_0))*vec(n) | / | vec(n)| =| vec(r_1) * vec(n) - vec(r_0) *vec(n) |/ |vec(n) | `
`=> p = |vec(r_1)* vec(n) -vec(d) | /| vec(n)|`
If equation of plane is `ax + by+ cz+ d =0` then perpendicular distance from point `(x_1, y_1, z_1)` is given by
` |ax_1 +by_1 +cz_1 +d |/ sqrt (a^2+b^2+c^2)`
`text(Note: )`
`(i)` Planes `a_1x + b_1y + c_1z + d_1 = 0` and `a_2x + b_2y + c_2z + d =0` are
`quadquadquad (a)` parallel but not identical if ` a_1/a_2 =b_1/b_2 =c_1/c_2 ne d_1/d_2`
`quadquadquad (b)` perpendicular if `a_1a_2 +b_1b_2+c_1c_2 =0`
`quadquadquad (c)` identical if `a_1/a_2=b_1/b_2 =c_1/c_2 =d_1/d_2`
`(ii)` The equation of a plane parallel to the plane `ax + by+ cz +d` is `ax+ by + cz + k = 0`, where `k` is an arbitrary constant and is determined by the given condition.
`(iii)` Distance between two parallel planes `ax + by+ cz + d_1 = 0` and `ax+ by + cz + d_2 = 0` is equal to
` |d_1-d_2 | /sqrt (a^2+b^2+c^2)`
`(iv)` `3` planes `a_rx + b_ry + c_rz = d_r` `r 1, 2, 3`
`quadquadquad (a)` Can intersect at a point`=` system of equations in `3` variables having unique solution.
`quadquadquad (b)` Can intersect coaxially`=` system of equations in `3` variables having infinite solutions.
`quadquadquad (c)` May not have a common point `=` system of equations in `3` variables having no solution.
e.g. To illustrate our approach for finding the distance between a point and a plane, we work through an example.
Find the distance from the point `P=(4,−4,3)` to the plane `2x−2y+5z+8=0` which is pictured in the below figure in its original view.
Solution: We use the second formula from the page on distance from a point to a plane. From the equation for the plane we substitute `A=2, B=−2,C=5,D=8.` From the point PP, we substitute `x_1=4, y_1,` and `z_1=3.` The distance from PP to the plane is
`d = |2⋅4+(−2)⋅(−4)+5⋅3+8|/sqrt(2^2+(−2)^2+5^2)= 6.8`