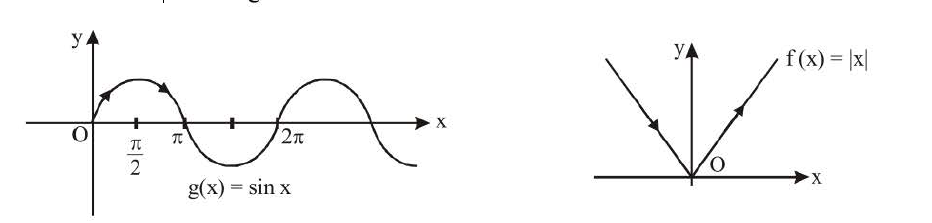
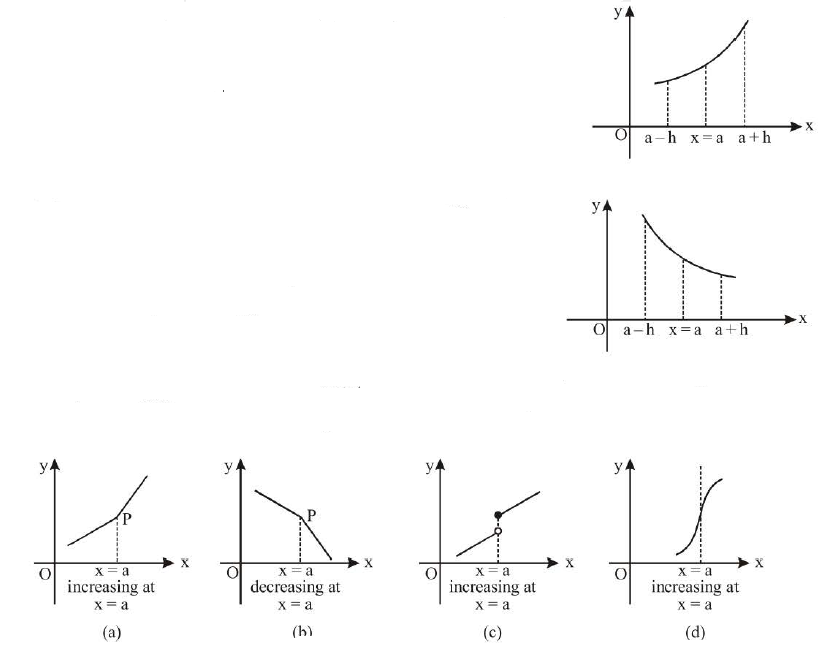
(a) Monotonic function :
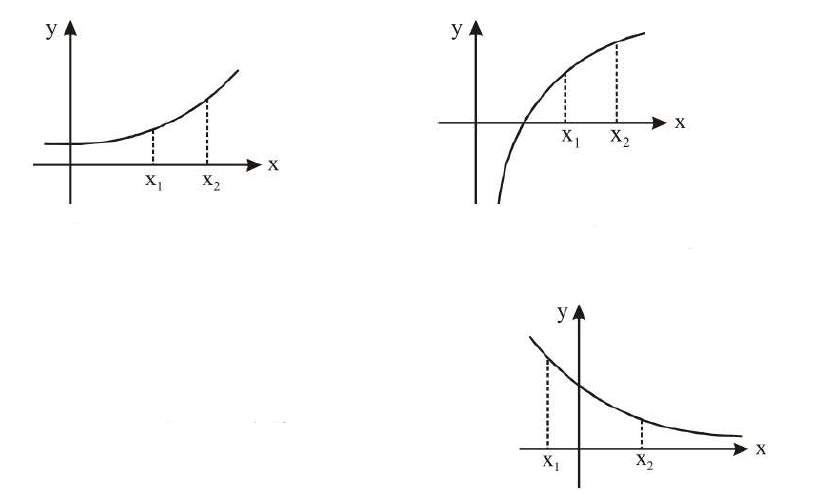
Functions are said to be monotonic if they are either increasing or decreasing in their entire domain
e.g. `f(x) = e^x ; f(x) = ln x` & `f(x) = 2x + 3` are some of the examples of functions which are increasing
where as `f(x) =- x^3 ; f(x) e^(-x)` and `f(x) = cot^(-1) (x)` are some of the examples of the functions which
are decreasing.
Increasing function :
If `x_1 < x_2` and `f(x _1) < f(x _2)` then function is called increasing function or strictly increasing function.
Decreasing function :
`f(x) = e^(-x)`
If `x_1 < x_2 `
but `f(x _1)> f(x_2)` in entire domain then fucntion is called
decreasing function or strictly decreasing function.
e.g. `f(x) = e^x ; f(x) = ln x` & `f(x) = 2x + 3` are some of the examples of functions which are increasing
where as `f(x) =- x^3 ; f(x) e^(-x)` and `f(x) = cot^(-1) (x)` are some of the examples of the functions which
are decreasing.
Increasing function :
If `x_1 < x_2` and `f(x _1) < f(x _2)` then function is called increasing function or strictly increasing function.
Decreasing function :
`f(x) = e^(-x)`
If `x_1 < x_2 `
but `f(x _1)> f(x_2)` in entire domain then fucntion is called
decreasing function or strictly decreasing function.