When vehicles go through turnings, they travel along a nearly circular arc. There must be some force which will produce the required centripetal acceleration. If the vehicles travel in a horizontal circular path, this resultant force is also horizontal. The necessary centripetal force is being provided to the vehicles in the fol lowing three ways.
a. By friction
b. By banking of roads
c. By both friction and banking of roads.
Now let us consider equations of motion in each of the three cases separately.
`text(By Friction Only :)`
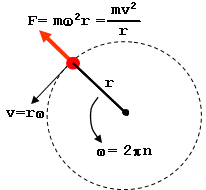
Suppose a car of mass m is moving at a speed v in a horizontal circular arc of radius r. In this case, the necessary centripetal force to the car will be provided by force of friction f acting towards centre.
Thus , `f = (mv^2)/r`
Further, limiting value of `f` is `mu N`
or `f_L = mu N = mu m g`
Therefore, for a safe turn without sliding `(mv^2)/r` `<=` `f_L`
or `(mv^2)/r` `<=` `mu m g ` or `mu` `>=` `v^2/(rg)` or `v` `<=` `sqrt(mu r g)`
`text(By Banking of Roads :)`
To avoid dependence on friction, the roads are banked at the turn so that the outer part of the road is lifted compared to the inner part.
Applying Newton's second law along the radius and the first law in the vertical direction.
`N sin theta = (mv^2)/r`
and `N cos theta = mg`
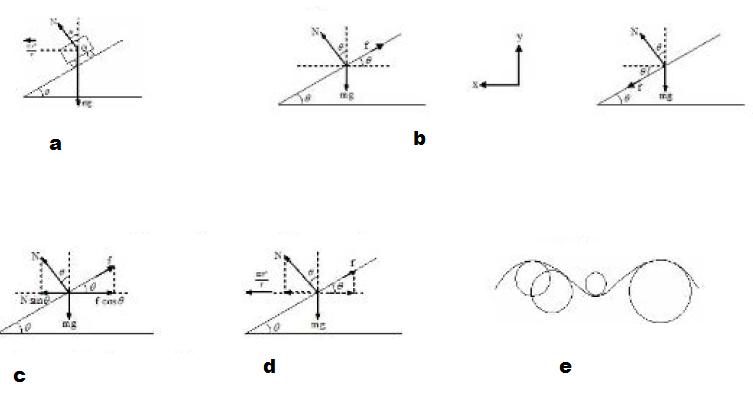
From these two equations. we get(FIG-a)
`tan theta = v^2/(rg)...................(1)`
or `v = sqrt(rg tan theta)..................(2)`
`text(Note :)` This is the speed at which car does not slide down even if track is smooth. If track is smooth and speed is less than `sqrt(r g tan theta)`, vehicle will move down so that `r` decreases and if speed is more than this, the vehicle will move up.
`text(By Friction and Banking of Road)`
If a vehicle is moving on a circular road which is rough and banked, then th ree forces act on the vehicle, of these the first force is weight `(mg)` , the second force, is normal reaction `N` and is perpendicular to road, the third force, is friction `f` which can be either inwards or outwards while its magnitude can be varied up to a maximum limit `(f_L = mu N)` .
i) Friction f is outwards if the vehicle is at rest or `v =0`. Because in this case the component of weight `mg sin theta` is balanced by `f`.
ii) Friction f is inwards if `v > sqrt(r g tan theta)`
iii) Friction fis outwards if `v < sqrt(r g tan theta)` and
iv) Friction `f` is zero if , `v = sqrt(r g tan theta)`
Let us now see how the force of friction and normal reaction change as speed is gradually increased. (fig-c,fig-d)
In figure (c) : When the car is at rest force of friction is upwards. We can resolve the forces in two mutually perpendicular directions. Let us resolve them in horizontal and vertical directions
`sumF_H = 0` `therefore` `N sin theta - f cos theta =0 ...................(1)`
`sum F_V = 0` `therefore` `N cos theta + f sin theta = mg .................(2)`
In figure (d) : Now the car is given a small speed `v`, so that a centripetal force `(mv^2)/r` is now required in `r`
horizontal direction towards centre. So equation (1) will now become,
`N sin theta - f cos theta = (mv^2)/r`
or we can say, in case (c) N sin and f cos were equal while in case (d) their difference is `(mv^2)/r`
N will increase and `f` will decrease. This is because equation number (2). `N cos theta + f sin theta = mg` is still to be valid, as there is no acceleration along vertical. So to keep `N cos + f sin` to be constant `(= mg) N` should increase and `f` should decrease `(as theta =` constant)
Now as speed goes on increasing, force of friction first decreases, becomes zero at `v= sqrt( r g tan theta)` and then reverses its direction.
`text(Maximum velocity with which a vehicle can take a turn on a rough banked road)`
`N sin theta +f cos theta = (mv_(max)^2)/R ; N cos theta = mg +f sin theta `
`f = mu N` (Velocity is maximum)
`N sin theta + mu N cos theta =(mv_(max)^2)/R.....................(1) `
`N cos theta = mg + mu N sin theta ...................(2)`
Solving for (1) & (2) , `V_(max) = sqrt((gR(sin theta +mu cos theta))/(cos theta +mu sin theta))`
`text(Radius of curvature)`
Any curved path can be assumed to be made of infinite circular arcs. Radius of curvature at a point is the radius of the circular arc at a particular point which fits the curve at that point.
`F_c = (mv^2)/R` or `R = (mv^2)/(f_c) = (mv^2)/F_(bot)`
`F_(bot) = ` Force perpendicular to velocity (centripetal force)
If the equation of trajectory of a particle is given we can find the radius of curvature of the instantaneous circle by using the formula,
`R =([1+ ((dy)/(dx))^2]^(3/2))/|(d^2y)/(dx^2)|`
fig-e
When vehicles go through turnings, they travel along a nearly circular arc. There must be some force which will produce the required centripetal acceleration. If the vehicles travel in a horizontal circular path, this resultant force is also horizontal. The necessary centripetal force is being provided to the vehicles in the fol lowing three ways.
a. By friction
b. By banking of roads
c. By both friction and banking of roads.
Now let us consider equations of motion in each of the three cases separately.
`text(By Friction Only :)`
Suppose a car of mass m is moving at a speed v in a horizontal circular arc of radius r. In this case, the necessary centripetal force to the car will be provided by force of friction f acting towards centre.
Thus , `f = (mv^2)/r`
Further, limiting value of `f` is `mu N`
or `f_L = mu N = mu m g`
Therefore, for a safe turn without sliding `(mv^2)/r` `<=` `f_L`
or `(mv^2)/r` `<=` `mu m g ` or `mu` `>=` `v^2/(rg)` or `v` `<=` `sqrt(mu r g)`
`text(By Banking of Roads :)`
To avoid dependence on friction, the roads are banked at the turn so that the outer part of the road is lifted compared to the inner part.
Applying Newton's second law along the radius and the first law in the vertical direction.
`N sin theta = (mv^2)/r`
and `N cos theta = mg`
From these two equations. we get(FIG-a)
`tan theta = v^2/(rg)...................(1)`
or `v = sqrt(rg tan theta)..................(2)`
`text(Note :)` This is the speed at which car does not slide down even if track is smooth. If track is smooth and speed is less than `sqrt(r g tan theta)`, vehicle will move down so that `r` decreases and if speed is more than this, the vehicle will move up.
`text(By Friction and Banking of Road)`
If a vehicle is moving on a circular road which is rough and banked, then th ree forces act on the vehicle, of these the first force is weight `(mg)` , the second force, is normal reaction `N` and is perpendicular to road, the third force, is friction `f` which can be either inwards or outwards while its magnitude can be varied up to a maximum limit `(f_L = mu N)` .
i) Friction f is outwards if the vehicle is at rest or `v =0`. Because in this case the component of weight `mg sin theta` is balanced by `f`.
ii) Friction f is inwards if `v > sqrt(r g tan theta)`
iii) Friction fis outwards if `v < sqrt(r g tan theta)` and
iv) Friction `f` is zero if , `v = sqrt(r g tan theta)`
Let us now see how the force of friction and normal reaction change as speed is gradually increased. (fig-c,fig-d)
In figure (c) : When the car is at rest force of friction is upwards. We can resolve the forces in two mutually perpendicular directions. Let us resolve them in horizontal and vertical directions
`sumF_H = 0` `therefore` `N sin theta - f cos theta =0 ...................(1)`
`sum F_V = 0` `therefore` `N cos theta + f sin theta = mg .................(2)`
In figure (d) : Now the car is given a small speed `v`, so that a centripetal force `(mv^2)/r` is now required in `r`
horizontal direction towards centre. So equation (1) will now become,
`N sin theta - f cos theta = (mv^2)/r`
or we can say, in case (c) N sin and f cos were equal while in case (d) their difference is `(mv^2)/r`
N will increase and `f` will decrease. This is because equation number (2). `N cos theta + f sin theta = mg` is still to be valid, as there is no acceleration along vertical. So to keep `N cos + f sin` to be constant `(= mg) N` should increase and `f` should decrease `(as theta =` constant)
Now as speed goes on increasing, force of friction first decreases, becomes zero at `v= sqrt( r g tan theta)` and then reverses its direction.
`text(Maximum velocity with which a vehicle can take a turn on a rough banked road)`
`N sin theta +f cos theta = (mv_(max)^2)/R ; N cos theta = mg +f sin theta `
`f = mu N` (Velocity is maximum)
`N sin theta + mu N cos theta =(mv_(max)^2)/R.....................(1) `
`N cos theta = mg + mu N sin theta ...................(2)`
Solving for (1) & (2) , `V_(max) = sqrt((gR(sin theta +mu cos theta))/(cos theta +mu sin theta))`
`text(Radius of curvature)`
Any curved path can be assumed to be made of infinite circular arcs. Radius of curvature at a point is the radius of the circular arc at a particular point which fits the curve at that point.
`F_c = (mv^2)/R` or `R = (mv^2)/(f_c) = (mv^2)/F_(bot)`
`F_(bot) = ` Force perpendicular to velocity (centripetal force)
If the equation of trajectory of a particle is given we can find the radius of curvature of the instantaneous circle by using the formula,
`R =([1+ ((dy)/(dx))^2]^(3/2))/|(d^2y)/(dx^2)|`
fig-e