LImit :

1. Concept Of Limits :
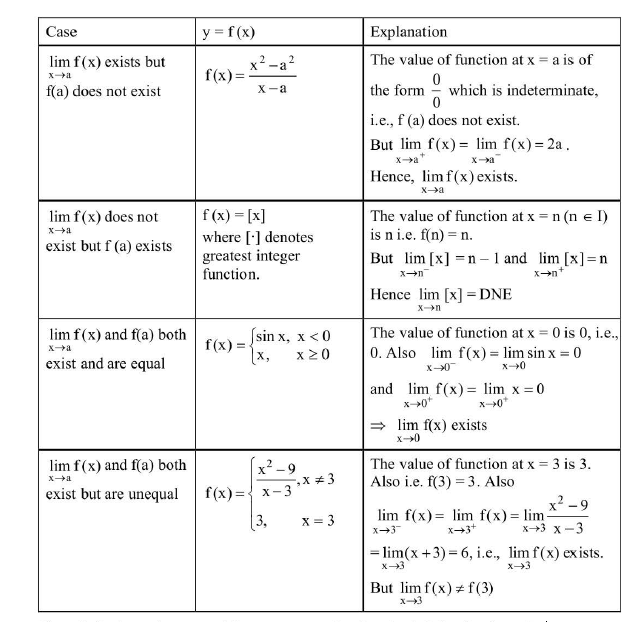
Suppose `f(x)` is a real -valued function `c` is a real number. The expression `lim_(x->c)f(x) = L` means that `f(x)` can be as close to `L` as desired by making `x` sufficiently close to `c`. In such a case, we say that limit of `f`, as `x` approaches `c`, is `L`. Note that this statement is true even if `f(c) ne L`. Indeed, the function `f(x)` need not even be defined at `c`. Two examples help illustrate this.
Consider `f(x) = x - 1` as `x` approaches 2. In this case, `f(x)` is defined at `2`, and it equals its limiting value `1`.
As `x` approaches `2`, `f(x)` approaches `1` and hence we have `lim_(x->2)f(x) =1`
`f(x) =(x^2-4)/(x-2)` tn this case `x` approaches `2` the limiting value of `f(x)` is equal to `4` even if `f(x)` is not defined at `x = 2`.
Thus, `f(x)` can be made arbitrarily close to the limit of `4` just by making `x` sufficiently close to `2`.
Suppose `f(x)` is a real -valued function `c` is a real number. The expression `lim_(x->c)f(x) = L` means that `f(x)` can be as close to `L` as desired by making `x` sufficiently close to `c`. In such a case, we say that limit of `f`, as `x` approaches `c`, is `L`. Note that this statement is true even if `f(c) ne L`. Indeed, the function `f(x)` need not even be defined at `c`. Two examples help illustrate this.
Consider `f(x) = x - 1` as `x` approaches 2. In this case, `f(x)` is defined at `2`, and it equals its limiting value `1`.
As `x` approaches `2`, `f(x)` approaches `1` and hence we have `lim_(x->2)f(x) =1`
`f(x) =(x^2-4)/(x-2)` tn this case `x` approaches `2` the limiting value of `f(x)` is equal to `4` even if `f(x)` is not defined at `x = 2`.
Thus, `f(x)` can be made arbitrarily close to the limit of `4` just by making `x` sufficiently close to `2`.