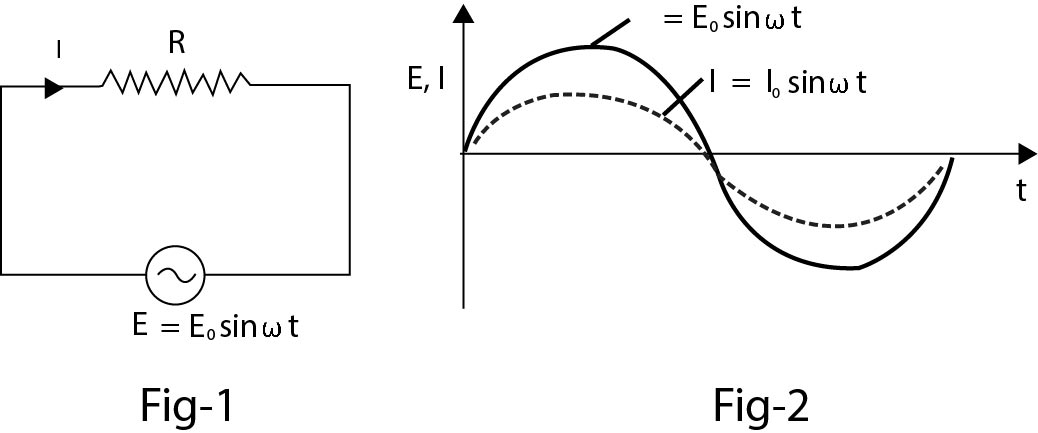
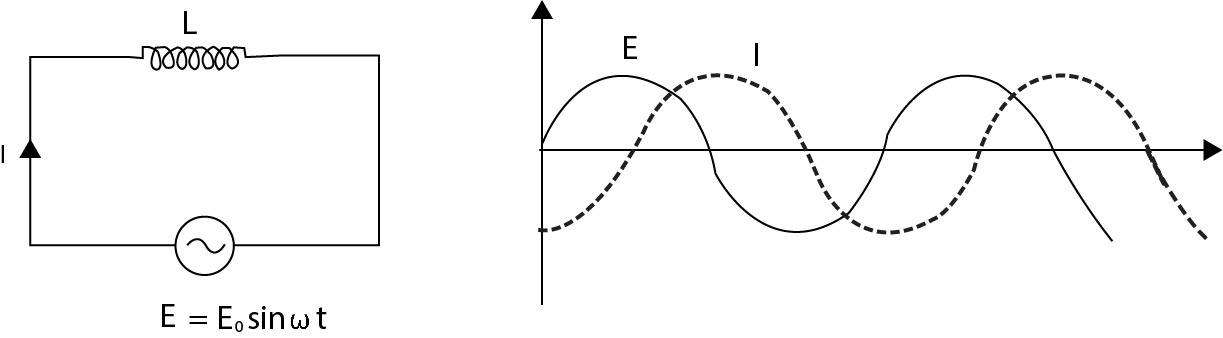
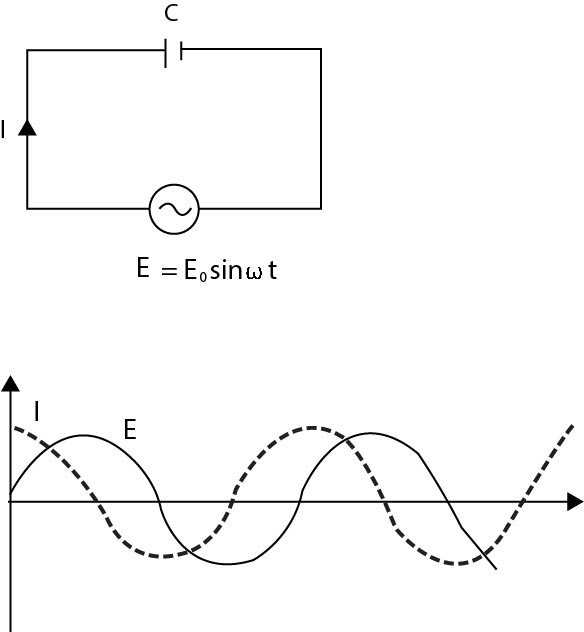
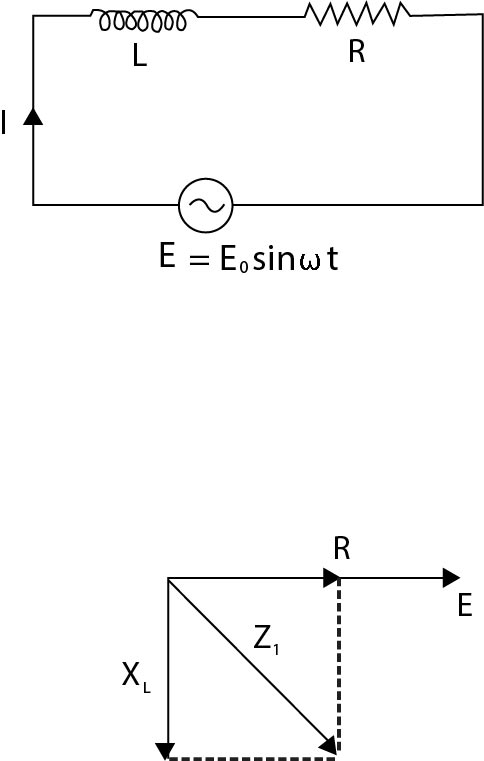
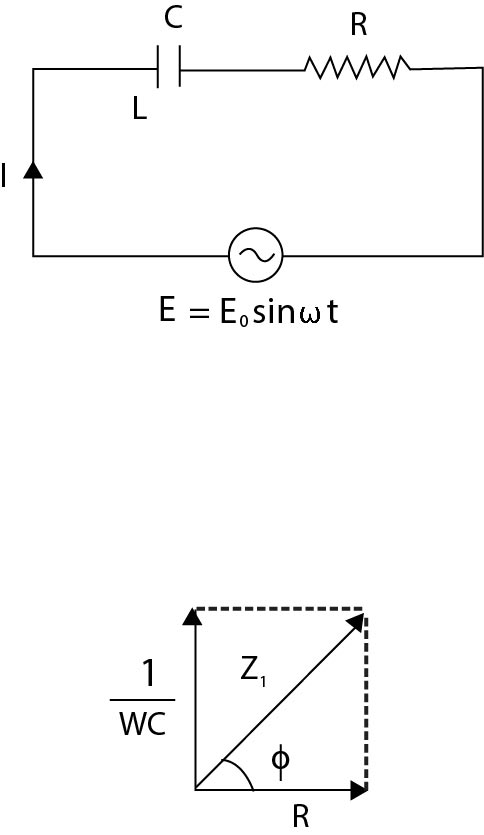
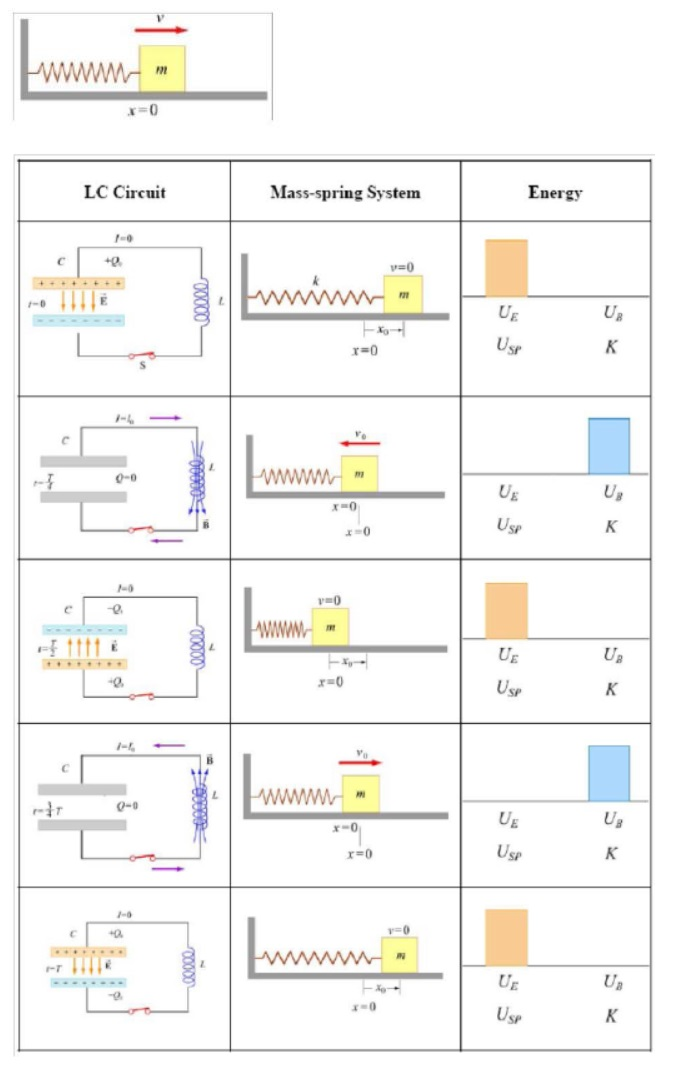
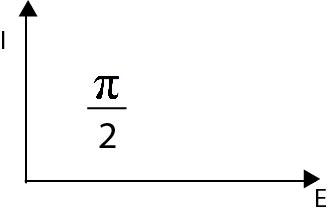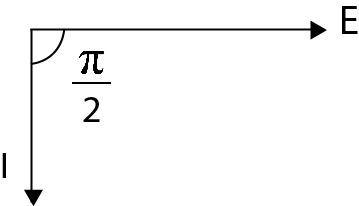Schematic Design
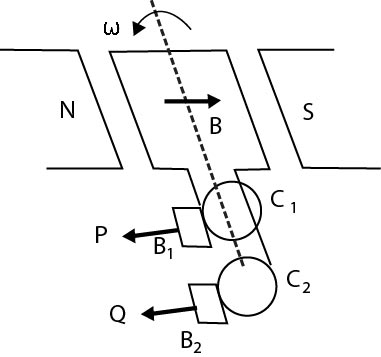
The Armature coil which is a rectangular coil of N turns
wound over a soft-iron core (to increase the
magnetization) is mounted on an axle along the
symmetry axis of the coiI that can be coupled to a
rotating wheel/turbine etc. A strong uniform magnetic
field produced by a permanent magnet or electromagnet
cuts through the rotating Armature coil as shown in the
figure. Notice that the axis of rotation for the Armature
coil is perpendicular to the magnetic field lines.
The Armature coil is also connected to two slip rings `C_1`
and `C_2` which in turn are in contact with two carbon brushes `B_1` and `B_2` such
that there is permanent electrical contact without hampering the
rotation of the coil . The brushes are connected to two
terminals P and Q which function as the output terminals
for the Generator and the external circuit is connected
across P and Q.
The armature coil is driven at a constant angular speed `omega`
such that at given instant, the angle between the coil's
area vector `vecA `and the magnetic field `vecB` is `theta = (omega t +phi)`,
therefore the magnetic flux, `phi_B=vecB.vecA` is given by the
relation.
`phi_B = NBACos(omega t+ phi)` . Hence, by application of Faraday's
law, the induced EMF (developed across the terminals P
and Q),
`E = - (dphi_B)/(dt) =NBA omega sin(omega t+phi)` which can be expressed as,
`E = E_0 sin (omega t +phi)` , where the term `E_0` is define as the
'peak' voltage given by `E_0 = NBA omega = NBA xx 2 pi f`.
It is important to note here that the peak voltage `E_0`
depends on not only the intensity of the magnetic field B,
the geometry of the Armature coil (N and A) but also on
the angular frequency `omega` (or frequency f) of rotation.
Household power supplied in India and most of
Asia/Europe is AC with an alternating frequency of 50 Hz.
In the sections following, various types of circuits using
resistors, capacitors and inductors connected across an
AC Source are analyzed
wound over a soft-iron core (to increase the
magnetization) is mounted on an axle along the
symmetry axis of the coiI that can be coupled to a
rotating wheel/turbine etc. A strong uniform magnetic
field produced by a permanent magnet or electromagnet
cuts through the rotating Armature coil as shown in the
figure. Notice that the axis of rotation for the Armature
coil is perpendicular to the magnetic field lines.
The Armature coil is also connected to two slip rings `C_1`
and `C_2` which in turn are in contact with two carbon brushes `B_1` and `B_2` such
that there is permanent electrical contact without hampering the
rotation of the coil . The brushes are connected to two
terminals P and Q which function as the output terminals
for the Generator and the external circuit is connected
across P and Q.
The armature coil is driven at a constant angular speed `omega`
such that at given instant, the angle between the coil's
area vector `vecA `and the magnetic field `vecB` is `theta = (omega t +phi)`,
therefore the magnetic flux, `phi_B=vecB.vecA` is given by the
relation.
`phi_B = NBACos(omega t+ phi)` . Hence, by application of Faraday's
law, the induced EMF (developed across the terminals P
and Q),
`E = - (dphi_B)/(dt) =NBA omega sin(omega t+phi)` which can be expressed as,
`E = E_0 sin (omega t +phi)` , where the term `E_0` is define as the
'peak' voltage given by `E_0 = NBA omega = NBA xx 2 pi f`.
It is important to note here that the peak voltage `E_0`
depends on not only the intensity of the magnetic field B,
the geometry of the Armature coil (N and A) but also on
the angular frequency `omega` (or frequency f) of rotation.
Household power supplied in India and most of
Asia/Europe is AC with an alternating frequency of 50 Hz.
In the sections following, various types of circuits using
resistors, capacitors and inductors connected across an
AC Source are analyzed