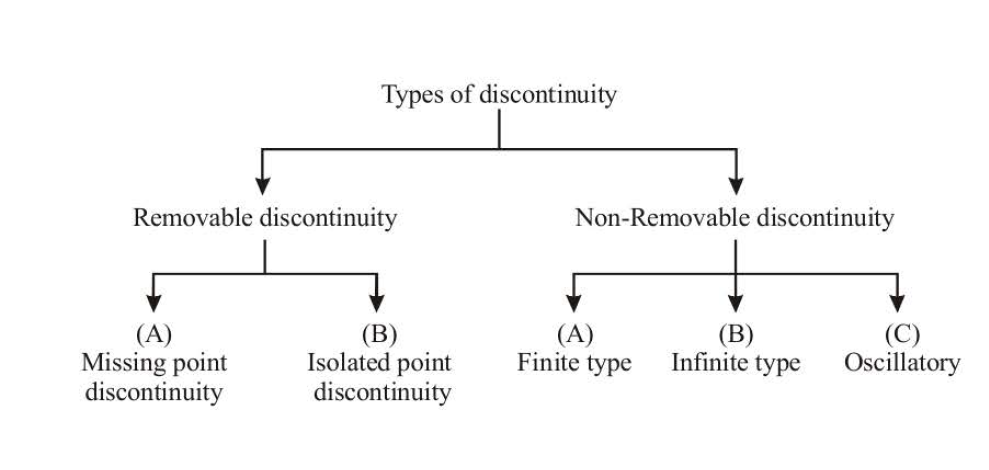
A function `f(x)` is said to be continuous at `x = a`,

if `Lim_(x->a)f(x) =f(a)`

`=>Lim_(h->0) f (a-h)= Lim_(h->0)f(a+h)=f(a)=a` finite quantity.

i.e. `LHL` at `x = a = RHL` at `x = a` = value of `f(x)` at `x = a` finite quantity.

`text(Note:)`

`(i)` Continuity at `x = a => ` existence of limit at `x = a`, but not the converse.

`(ii)` Continuity at `x = a =>` `f` is well defined at `x = a`, but not the converse.

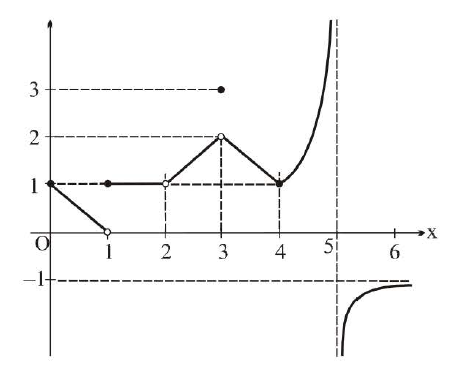
`(iii)` Discontinuity at `x=a` is meaningful to talk if in the immediate neighborhood of
`x = a`, i.e. the function has a graph in the immediate neighborhood of `x = a`, not necessarily at `x = a`.

`(iv)` Continuity is always talk in the domain of function and hence `f(x) =1/x-1 ,1/x, tan x` are all continuous
functions but if you want to talk of discontinuity then we can say `1/(x-1)` is discontinuous at `x=1, 1/x` is
discontinuous at `x = 0`.

Note that all rational functions are continuous. Because continuity is always talk in the domain of `f(x)`.

`(v)` Point function are continuous.
e.g. `sqrt (1-x) + sqrt (x-1) , sqrt (x) +sqrt (-x)`

`(vi)` Inverse of a discontinuous function can be continuous.

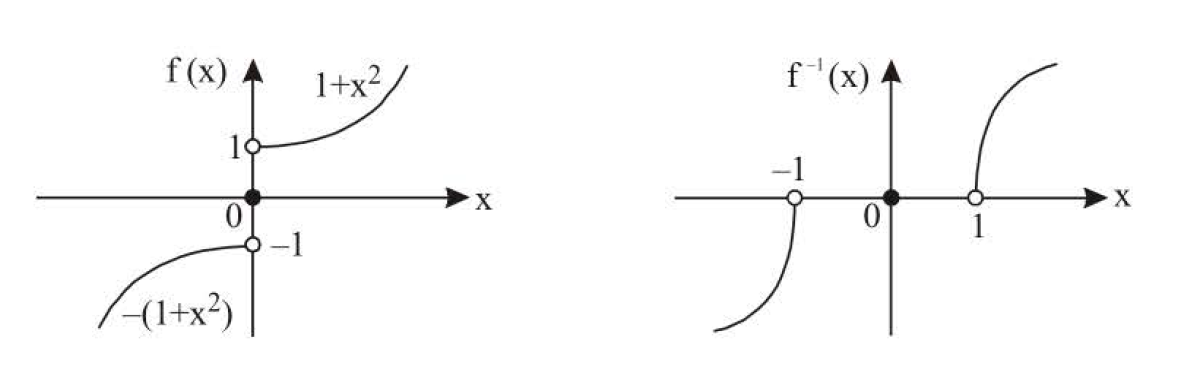
e.g. `f(x) = [tt( (1+x^2, text(if) x ne 0) , ( 0 , text(if) x=0) , (-(1+x^2) ,text(if) x ne 0) )` is discontinuous at `x = 0` but its inverse function

`f^(-1) (x) = [tt( ( sqrt(x-1) , text(if) x>1 ) ,(0, text(if) x=0) ,(sqrt (- (1+x)) , text(if) x <-1) )` which is a continuous function and its graph is as shown.

`(a)` A function `f` is said to be continuous in `(a, b)` if `f` is continuous at each & every point `in (a. b)`.

`(b)` A function `f` is said to be continuous in a closed interval `[a , b]` if:

` quad quad quad quad quad quad quad(i) ``f` is continuous in the open interval `(a, b)` &

` quad quad quad quad quad quad quad(ii)` `f` is right continuous at ` a ` i.e., `Lim_(x->a^+) f(x) =f(a) =a` finite quantity .

` quad quad quad quad quad quad quad quad(iii) ` `f` is left continuous at ` b ` i.e., `Lim_(x->b^-) f(x) =f(b)=a` finite quantity.

A function can be discontinuous due to the following reasons.

`(i)` `Lim_(x->a) f(x)` does not exist (`f(a)` may or may not be defined)

i.e., `Lim_(h->0) f(a+h) ne Lim_(h->0) f(a-h)`

e.g. `f(x)= [x]` discontinuous at all integer points `f(x) = sgn x` discontinuous at `x =0`

`f(x) =x /(x-1)` discontinuous at `x = 1`.

`(ii)` `Lim_(x->a) f(x) ` exist but is not equal to `f(a)` i.e `Lim_(h->0) f(a+h) = Lim_(h->0) f(a-h) ne f(a)`.

EX. `f(x) = [ tt ( ( (1-x) tan ((pi x)/2) , text(if) x ne 1 ) , (pi/2 , text (if) x=1 ) )`

`Lim_(x->1) f(x) =Lim_(x->1) (1-x) tan ((pi x)/2) = Lim_(h->1) ( -h/(tan ( (pi h)/a )) ) = 2/pi`


`=> Lim_(x->1) f(x) ne f(1) => f(x)` is discontinuous at `x = 1`.


`(iii)` `f(a)` is not defined

e.g. `f(x) =1/(x-1)`

(iv) To understand explicitly the reasons of discontinuity. Consider the following graph of a function.

`quadquad quadquadquadquadquad(a)` `f` is continuous at `x = 0` and `x = 4`
`quadquadquadquadquadquadquad(b)` `f` is discontinuous at `x = 1` as limit does not exist
`quadquadquadquadquadquadquad(c)` `f` is discontinuous at `x = 2` as `f (2)` is not defined although limit exist.
`quadquadquadquadquadquadquad(d)` `f` is discontinuous at `x = 3` as `Lim_(x->3) f(x) ne f(3)`
`quadquadquadquadquadquadquad(e)` `f` is discontinuous at `x = 5` as neither the limit exist nor `f` is defined at `x = 5`.


`text(Note:)`

`(i)` Every polynomial function is continous at every point of the real line.
`f(x) =a_0x^n +a_1x^(n-1) +a_2x^(n-2) + ......+a_n AA x in R`

`(ii)` Every rational function is continuous at every point where its denominator is different from zero.

`(iii)` Logarithmic functions, exponential functions, trigonometric functions, inverse circular functions, and
modulus functions are continuous in their domain.

Here `lim_(x->a) f(x)` necessarily exists, but is either not equal to `f(a)` or `f(a)` is not defined. In this case,
therefore it is possible to redefine the function in such a manner that `Lim_(x-.a) f(x) =f(a)` and thus making
the function continuous. These discontinuities can be further classified as

(A) Missing point discontinuity :

Here `Lim_(x->a) f(x)` exists. But `f(a)` is not defined.

(a) `f(x) =( ((x-1) (9-x^2) )/(x-1) ) x ne 1`

at `x = 1, f(1)` is not defined. Hence `f(x)` has missing point of discontinuity at `x = 1`.

(b) `f(x) =( (x^2 -4)/(x-2) ) x ne 2`

`f(2)` is not defined. Hence, `f(x)` has missing point of discontinuity at `x = 2`.

(c) `f(x) =(sin x)/x , x ne 0`
`f(0)` is not defined. `f(x)` has missing point of discontinuity at `x = 0`.

Here `Lim_(x->a) f(x) ` exists, also `f(a)` is defined but `Lim_(x->a) f(x) ne f(a)`


(a) `f(x) = [x] + [-x] = [ tt ( (0, text(if) x in I) , (-1 , text(if) x notin I) )`

has isolated point of discontinuity at all integeral points.

(b) `f(x) = sgn (cos 2 x - 2 sin x + 3 ) =
sgn ( 2 ( 2 + sin x) ( 1 - sin x) )
= [ tt ( (0,text (if) x=2n pi + (pi/2)) , ( +1, text(if) x ne 2 n pi +(pi/2)) ) `

has an isolated point at `x =0` discontinuity as `x = 2 n pi + pi/2`

Here `Lim_(x->a) f(x)` does not exists and therefore it is not possible to redefine the function in any manner to
make it continuous. Such discontinuities can be further classified into 3 fold.

(a) Finite type (both limits finite and unequal)

(i) `Lim_(x->0) tan^(-1) (1/x)= [tt( (f(0^+) =pi/2) , ( f(0^-) = - pi/2) )` ; jump `= pi`

(ii) `Lim_(x->0) (|sin x |/x)= [tt( (f(0^+) =1) , ( f(0^-) = - 1) )` ; jump `= 2`

(iii) `Lim_(x->2) ( [x]/x) =[tt( (f(2^+) = 1) , ( f(2^-) = - 1/2) )` ; jump `= 1/2`

In this case non negative difference between the two limits is called the Jump of discontinuity. A function
having a finite number of jumps in a given interval `I` is called a Piece Wise Continuous or Sectionally
Continuous function in this interval.

(i) `f(x) = (x/(1-x))` at `x=1 ,[tt( (f(1^+) =-oo) , ( f(1^-) = + oo) )`

(i) `f(x) = 2^(tanx)` at `x=pi/2 ,[tt( (f((pi/2)^+) =0) , ( f((pi/2)^-) = oo) )`

(i) `f(x) = (1/(x^2))` at `x=0 ,[tt( (f(0^+) =oo) , ( f(0^-) = oo) )`

(i) ` tt ( (f(x) =sin( 1/x) ) ,( text (or)) ,( f(x) =cos (1/x)) ) ]` at `x=0` oscillates between `- 1` & `1`



(ii) `f(x) = [ 1+ 1/3 sin ( ln |x |)] ` at `x=0` oscillates between `0` & `1`.

T -1 : Sum, difference, product and quotient of two continuous functions is always a continuous function.

However `h(x) = f(x) /g(x) ` is continuous at `x=a` only if `g(a) ne 0`

(a) lf `f(x)` is continuous and `g (x)` is discontinuous then prove that `f(x) + g (x)` is a discontinuous function.

Proof: Let `f(x) + g(x)` is a continuous function.

so, `Lim_(x->a) ( f(x) = g(x) )= f(a) +g(a)` .........................................(1)

Also, `f(x)` is a continuous function `Lim_(x->a) f(x) + g(a)` ........................(2)

From `(1)` and `(2)`

`Lim_(x->a) g(x) = g (a) => g(x) ` is continuous at `x =a`.

But given `g(x)` is discontinuous at `x = a`.

Hence by contradiction `f(x) + g(x)` is discontinuous function.

`(i)` `f(x) = x ` & `g(x) = [tt ( (sin 1/x , x ne 0) ,(0, x=0) ) `

Then `f(x) * g(x) = { tt ( (x sin (1/x) , x ne 0) ,( 0, x =0) )` is continuous at `x = 0`.

`(ii)` `f(x) = cos ( (2x -1) /2) pi` is continuous at `x = 1` and `g(x) = [x]` and `[.]` denotes the greatest integer
functions is discontinuous at `x =1` but `f(x) *g(x)` is continuous at `x = 1`.

`Lim_(x -> 1^+) cos ( (2x-1)/2) pi*[x] =cos pi/2 * (1) =0`

`Lim_(x->1^+) cos ( (2x-1)/2) pi*[x] =cos (pi/2) * (0) = 0, f(1) =0 =>` continuous at `x = 1`.

`f(x) = - g(x) = [tt ( (1, x ge 0) , (-1 , x <0)) `

`:.` `f(x) g(x) =1 AA x in R` which is continuous function.

If `f` is continuous on `[a, b]` and `f (a) ne f (b)` then for any value `c in ( f( a ), f(b))` , there is at least one
number `x_0` in `(a, b)` for which `f(x_0) =c`


`text(NOTE :)`

`(1)` Continuity through the interval `[a, b]` is essential for the validity of this theorem.

`(2)` in figure-3 , `f(a)` and `f(b)` are of opposite sign but `f(x)` has no root in `(a, b)` as `f` is continuous.

If `f` is continuous on `[a, b]` then `f` takes on, a least value of `m` and a greatest value `M` on this interval.

Note :To see that continuity is necessary for the extreme value theorem to be true refer the graph
shown.

There is a discontinuity at `x =c` interval. The function
has a minimum value at the left end point `x = a` and `f`
has no maximum value.

`(i)` If `a` function `f` is continuous on a closed interval `[a, b]` then it is bounded.

`(ii)` A continuous function whose domain is some closed interval must have its range also in closed interval.

`(iii)` If `f` is continuous and onto on `[a, b]` and is onto then `f^( - 1)`(from the range of `f` ) is also continuous.

`(iv)` If `f(a)` and `f(b)` possess opposite signs then `3` at least one solution of the equation `f(x) = 0` in the open
interval `(a, b)` provided `f` is continuous in `[a, b]`.

Continuity of functions in which greatest integer function is involved:

`f(x) = [x]` is discontinuous when `x` is an integer.

Similarly, `f(x)= [g(x)]` is discontinuous when `g(x)` is an integer, but this is true only when `g(x)` is monotonic

`g(x)` is strictly increasing or strictly decreasing).

For example, `f(x) = [ sqrty x]` is discontinuous when `sqrt x` is an integer, as `sqrtx` is strictly increasing (monotonic function).

`f(x) = [x^2], x ge 0` is discontinuous when `x^2` is an integer, as `x^2` is strictly increasing for `x ge 0.`



Now consider, `f(x)= [sin x] , x in [0, 2pi]*g(x) = sin x` is not monotonic in `[0, 2pi]`.
Forth is type of function, points of discontinuity can determined easily by graphical methods. We can
note that at `x =(3pi)/2` , `sin x` takes m tegral value `-1` but at `x= (3pi)/2` , `f(x) = [sin x]` is continuous.

We know that `f(x) = sgn (x)` is discontinuous at `x = 0`.
In general, `f(x) = sgn (g (x))` is discontinuous at `x = a` if `g(a) = 0`.

We know that `lim_(n->oo) a^n = { tt ( (0, 0 le a <1) ,(1, a=1) ,(oo , a > 1))`

If `f` is continuous at `x = a` & `g` is continuous at `x = f(a)` then the composite `g[f(x)] `is continuous at

`x =a` e.g., `f(x) = ( xsin x)/(x^2 +2)` & `g(x) = |x |` are continuous at `x = 0`. hence the composite

`(gof) (x) = |( x sin x)/(x^2+2) |` will also be continuous at `x =0`.