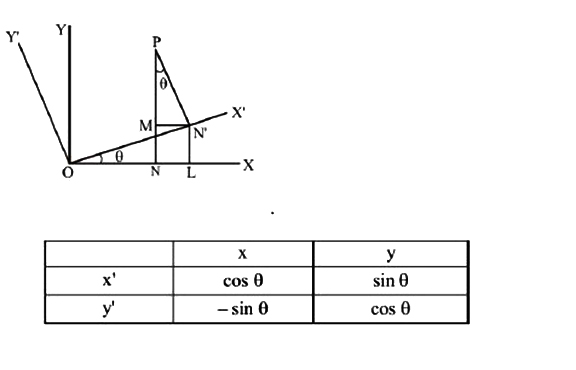
SHIFTING OF ORIGIN :
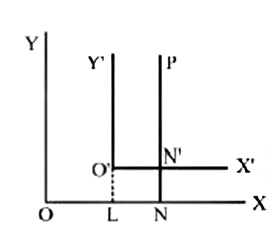
Let `OX` and `OY` be the original axes and let the new axes, parallel to the original, be `O'X'` and `O'Y'`
Let the coordinates of the new origin `O',` referred to the original axes be `h` and `k,` so that, if `O'L` be
perpendicular to `OX`, we have
`OL = h` and `LO' = k`
Let `P` be any point in the plane of the paper, and let its coordinates, referred to the original axes, be `x` and
`y` and referred to the new axes let them `x'` andy'.
Draw `PN` perpendicular to `OX` to meet `O'X'` in `N'.`
then, `ON = x, NP = y, O'N' = x'` and `N'P = y'`
we therefore, have
`x = ON = OL + O'N' = h + x'`
and `y = NP = LO' + N'P = k + y'`
The origin is therefore, transferred to the point `(h, k)`
when we substitute for the coordinates `x` and `y` the
quantities.
`x' + h andy' + k`
The above article is true whether the axes be oblique or rectangular.
Let the coordinates of the new origin `O',` referred to the original axes be `h` and `k,` so that, if `O'L` be
perpendicular to `OX`, we have
`OL = h` and `LO' = k`
Let `P` be any point in the plane of the paper, and let its coordinates, referred to the original axes, be `x` and
`y` and referred to the new axes let them `x'` andy'.
Draw `PN` perpendicular to `OX` to meet `O'X'` in `N'.`
then, `ON = x, NP = y, O'N' = x'` and `N'P = y'`
we therefore, have
`x = ON = OL + O'N' = h + x'`
and `y = NP = LO' + N'P = k + y'`
The origin is therefore, transferred to the point `(h, k)`
when we substitute for the coordinates `x` and `y` the
quantities.
`x' + h andy' + k`
The above article is true whether the axes be oblique or rectangular.