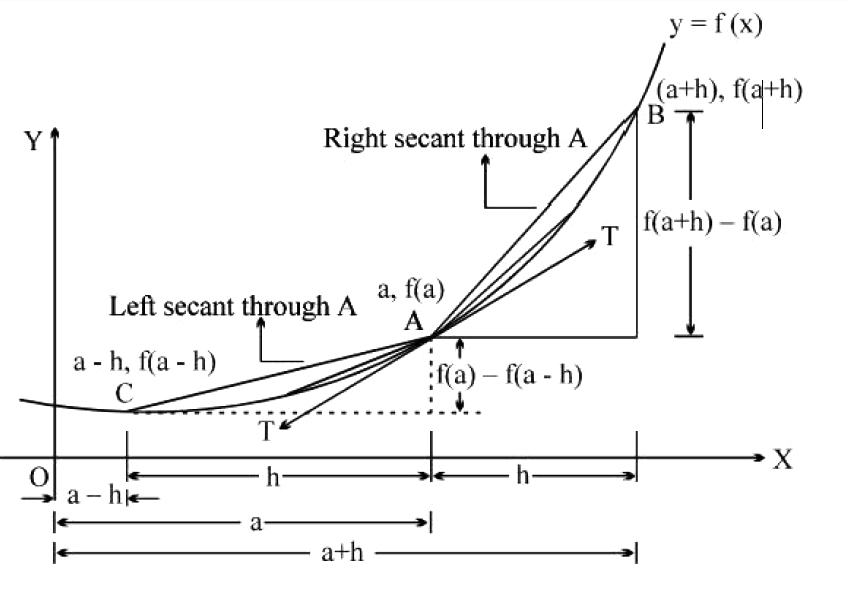
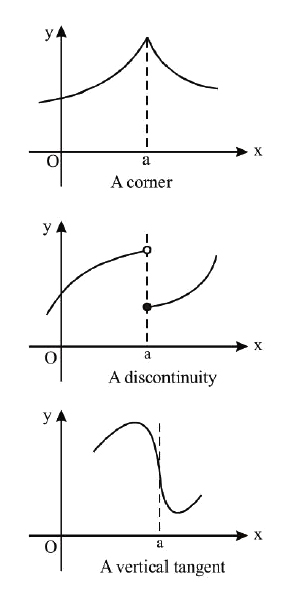
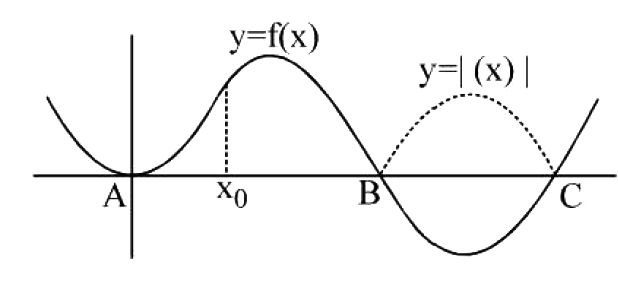
lf `f(x)` and `g (x)` both are derivable at `x = a`, then
(i) `f(x) pm g(x) ` will be differentiable at `x = a`.
(ii) `f(x) *g(x) ` will be differentiable at `x = a`.
(iii) `f(x) /g(x)` w1ll be d1fferentmble at `x = a` Jf `g(a) ne 0`
Note that:
(1) lf `f(x)` and `g (x` )are both derivable at `x=a , f(x) pm g(x) ; g(x) * f(x)` and `f(x) /g(x)` will also bederivableat
`x = a`. (only if `g (a) ne 0`)
(2) lf `f(x)` is derivable at `x = a` and `g (x)` is not derivable at `x = a` then the `f(x) + g (x)` or `f(x)- g (x)` will not
be derivable at `x = a`.
e.g. `f(x) = cos | x |` is derivable at `x = 0` and `g (x) = | x |` is not derivable at `x = 0`,
then `cos | x | + | x |` or `cos | x | - | x |` will not be derivable at `x = 0`.
However nothing can be said about the product function in this case.
`f(x) = x` derivable at `x = 0`
`g (x) = | x |` not derivable at `x = 0`
`x | x | = [tt( (x^2, text (if) x ge 0) ,(-x^2, text(if) x < 0))`
(3) If both `f (x)` and `g (x)` are non derivable then nothing definite can be said about the
sum /difference / product function.
e.g. `f(x) = sin | x |` not derivable at `x = 0`
`g (x) = | x |` not derivable at `x = 0`
then the function
`F (x) = sin | x | - | x |` is derivable at `x = 0`
`G (x) = sin | x | + | x |` is not derivable at `x = 0`.
(4) lf `f(x)` is derivable at `x =a` and `f(a) = 0` and `g (x)` is continuous at `x = a` then the product function
`F (x) = f(x) * g (x)` will be derivable at `x = a`
`F' (a^+) =Lim_(h->0) ( f (a=h) g (a+h) -0)/h= f' (a) *g(a)`
`F' (a^-) = Lim_(h->0) ( f(a-h) g (a-h) -0 )/-h = f '(a) *g(a)`
(5) Derivative of a continuous function need not be a continuous function
`f(x) = {tt( ( x^2sin(1/x) , text(if) x ne 0 f'(0^+) =0) , (0, text (if) x=0 ; f' (0^-) =0) )`
`f(x) = {tt( (sin(1/x) * 2x-x^2 cos (1/x) (-1/x^2) , x ne 0) , ( 0 , text(if) x=0) )`
`f' (x)` is not continuous at `x = 0`.
lf `f(x)` and `g (x)` both are derivable at `x = a`, then
(i) `f(x) pm g(x) ` will be differentiable at `x = a`.
(ii) `f(x) *g(x) ` will be differentiable at `x = a`.
(iii) `f(x) /g(x)` w1ll be d1fferentmble at `x = a` Jf `g(a) ne 0`
Note that:
(1) lf `f(x)` and `g (x` )are both derivable at `x=a , f(x) pm g(x) ; g(x) * f(x)` and `f(x) /g(x)` will also bederivableat
`x = a`. (only if `g (a) ne 0`)
(2) lf `f(x)` is derivable at `x = a` and `g (x)` is not derivable at `x = a` then the `f(x) + g (x)` or `f(x)- g (x)` will not
be derivable at `x = a`.
e.g. `f(x) = cos | x |` is derivable at `x = 0` and `g (x) = | x |` is not derivable at `x = 0`,
then `cos | x | + | x |` or `cos | x | - | x |` will not be derivable at `x = 0`.
However nothing can be said about the product function in this case.
`f(x) = x` derivable at `x = 0`
`g (x) = | x |` not derivable at `x = 0`
`x | x | = [tt( (x^2, text (if) x ge 0) ,(-x^2, text(if) x < 0))`
(3) If both `f (x)` and `g (x)` are non derivable then nothing definite can be said about the
sum /difference / product function.
e.g. `f(x) = sin | x |` not derivable at `x = 0`
`g (x) = | x |` not derivable at `x = 0`
then the function
`F (x) = sin | x | - | x |` is derivable at `x = 0`
`G (x) = sin | x | + | x |` is not derivable at `x = 0`.
(4) lf `f(x)` is derivable at `x =a` and `f(a) = 0` and `g (x)` is continuous at `x = a` then the product function
`F (x) = f(x) * g (x)` will be derivable at `x = a`
`F' (a^+) =Lim_(h->0) ( f (a=h) g (a+h) -0)/h= f' (a) *g(a)`
`F' (a^-) = Lim_(h->0) ( f(a-h) g (a-h) -0 )/-h = f '(a) *g(a)`
(5) Derivative of a continuous function need not be a continuous function
`f(x) = {tt( ( x^2sin(1/x) , text(if) x ne 0 f'(0^+) =0) , (0, text (if) x=0 ; f' (0^-) =0) )`
`f(x) = {tt( (sin(1/x) * 2x-x^2 cos (1/x) (-1/x^2) , x ne 0) , ( 0 , text(if) x=0) )`
`f' (x)` is not continuous at `x = 0`.