Note:
In deriving the above expression for P.E or T.E at mean position is assumed to be zero. However if the system has
some non zero P.E.
At mean position, It should be taken into account to determine P.E. and T.E.
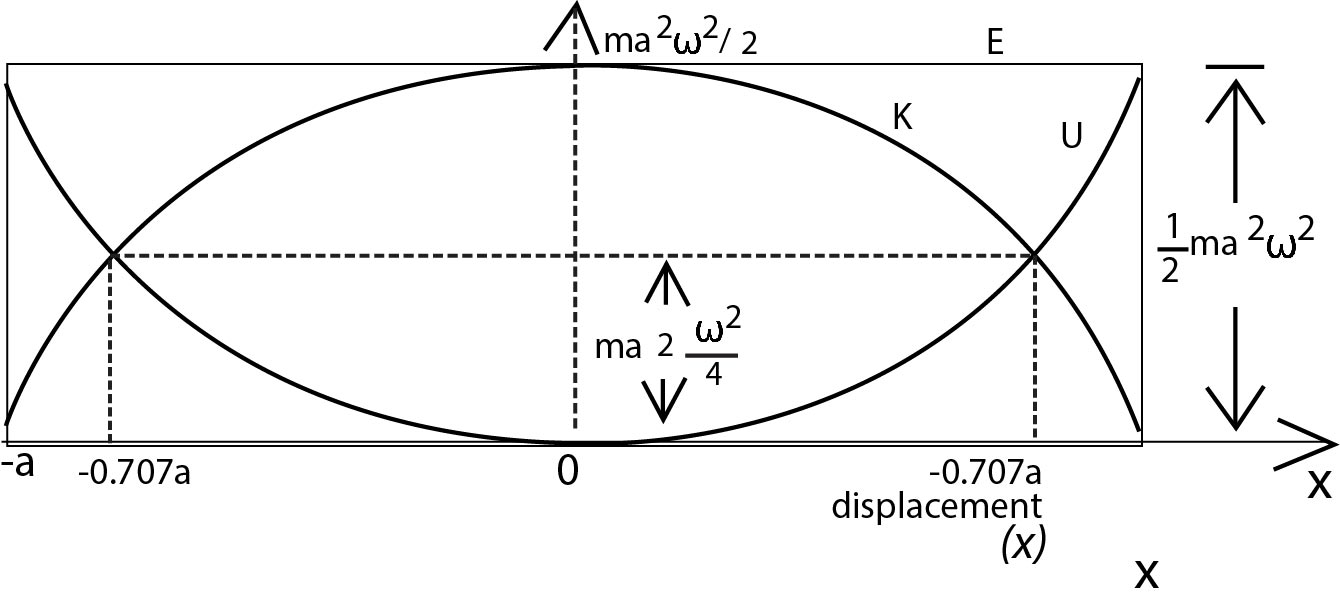
The expression for K.E. is independent of the choice of P.E. at mean position. Figure below shows the graphical variation of
K.E., P.E. and T.E. with displacement.
The curves of `K` and `U` intersect at `x` given by
`1/2 m omega^2(a^2-x^2) = 1/2 m omega^2 x^2`
`2x^2 = a^2=>x = 0.707 a`
and the corresponding `K` or `U` will be
`K = U = 1/2 [E] = 1/2 m omega^2 a^2`
some non zero P.E.
At mean position, It should be taken into account to determine P.E. and T.E.
The expression for K.E. is independent of the choice of P.E. at mean position. Figure below shows the graphical variation of
K.E., P.E. and T.E. with displacement.
The curves of `K` and `U` intersect at `x` given by
`1/2 m omega^2(a^2-x^2) = 1/2 m omega^2 x^2`
`2x^2 = a^2=>x = 0.707 a`
and the corresponding `K` or `U` will be
`K = U = 1/2 [E] = 1/2 m omega^2 a^2`