(a) Change of time period T due to a change in effective length.

[Law of lengths] `Tpropl` [other things remaining constant]

(i) If a child sitting on a swing stands up, then the effective length `l` decreases, due to an uplift of the centre of gravity of the system. This reduces the time period consequently.

(ii) If a hollow sphere filled with a liquid, and having a hole at its base, be made the bob of a simple pendulum, the time period, initially
increases, due to an increase in the effective length as the centre of gravity gets lowered due to the outflow of liquid from the sphere. The time period once again, gets restored, when the whole liquid flows out, due to the fact that the centre of gravity once again, comes to the centre of the sphere.

(iii) If the string be elastic with Young's modulus `Y`, then the length of pendulum will be `l + dl` [where `l` is the original length and `dl` increase in length]
From `Y = text(stress)/text(strain)` `=> Y = (mgl)/(a xx Deltal)` [where `M` is the mass of the bob]

`(Deltal)/l = (Mg)/(AY)`
Net length `= l(1+ (Deltal)/l) = l(1+ (Mg)/(AY))`

Now Time period `T = 2 pi sqrt(l/g(1+(Mg)/(AY)))`
Now, since `Mg < < AY`

`(Mg)/(AY) < < 1`

`T = 2 pi sqrt{(l/g)(1-(Mg)/(2AY))}` [From Binomial expansion]

Obviously, the time period increases, in this case.

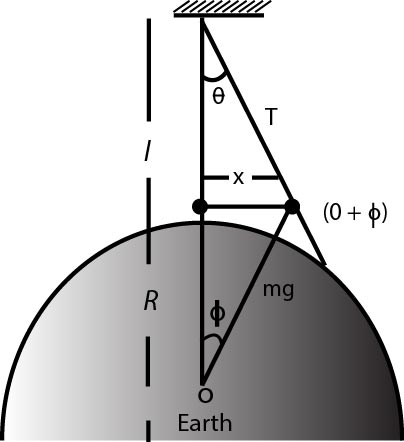
(iv) If the effective length be comparable to the radius of earth. (Figure)

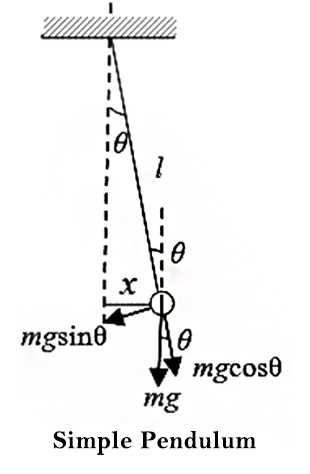
The net unbalanced force on the bob `= m (gsintheta+f)`


`F = mg(theta+f/g)`

`vecF =-mg(vecx/l -vecx/R) = -mg(1/l -1/R)vecx`

or acc. `f = -g(1/l-1/R)`

which is of the form of `vecf =-omega^2vecx` indicating that the bob, still executes SHM and its time period is not infinity. Comparing the above equation with std. form

`omega^2 = g(1/l -1/R)`

Time period `T = 2pi sqrt(1/(g(1/l-1/R)))`

Putting `l = R`, we can determine, the corresponding
time period as

`T = 2 pi sqrt(R/(2g)) > >1` hr

If `l` be too large
`T = 2 pi sqrt(R/(2g)) > >84.6` min.

If `I` be too small compared to earth's radius, then neglecting `1/R` in comparison to `1/l`
`T = 2 pi sqrt(l/g)` as derived earlier.

`T = mu 1/sqrtg` [other things remaining constant]

If a simple pendulum be taken to higher altitudes, its time period increases due to a decrease in the value of g. Consider a place P at
height 'h' above the earth's surface.

The value of g at that place g' (say) is given by :

`g' = (gR^2)/(R+h)^2 `
where g = acc. due to gravity on the earth's surface.
Time period `T = 2 pi sqrt(l/g)`
`2pisqrt((l(R+h)^2)/(gR^2))`

`T = 2pi ((R-h)/R) sqrt(l/g) = 2 pisqrt(l/g)(1+h/R)`

Now, if `h < < R` or `h/R < < 1`

Then `T = 2pi sqrt(l/(g(1+ h/R)^-2)) = 2psqrt(l/(g(1-(2h)/R))) `

(ii) If a simple pendulum be taken to a place below the earth's surface, the time period increases as a consequence of decrease in the value of acceleration due to gravity.

Consider a place `P` at a depth 'd' below the earth's surface, the acc. due to gravity at P is given
by :
`g' = g((R-d)/R)` [where g is the ace. due to gravity on the earth's surface)
Now, time period `T = 2 pi sqrt(l/g) =2pisqrt((lR)/(g(R-d)))`

(iii) If a simple pendulum at equator, be shifted to poles, the time period decreases on account of an increase in the value of 'g'. (acc. due to gravity is more at poles compared to equator).

The time period of a simple pendulum in a satellite within a freely falling lift is infinite (or the pendulum does not oscillate due to the absence of any restoring force, rending the bob to bring back to the mean position), on account of the fact that the value of `g` is zero.

(v) For a simple pendulum oscillating in a lift moving up with an acceleration a or down with `a` retardation a the effective value of g (say g) will be
`g = g +a`

`T = 2 pi sqrt(l/(g+a))`

The time period always decreases.

For a simple pendulum, oscillating in a lift moving down with an acceleration `a` or moving up with a
retardation `a`, the effective value of g (say g') will be `g' = (g - a)` down if `g > a` or `(a - g)` up if `a >g`.

For a simple pendulum oscillating in a vehicle accelerating with an acceleration 'a', the time period decreases due to an increase in the value of `g`

Let us first determine the equilibrium position of the string . If a be the angle made by string with vertical,

then : `T costheta = mg` and `T sintheta = m a`
Dividing `tantheta= a/g`
(opposite to the direction of acceleration of vehicle)
Effective external force `= msqrt(a^2+g^2)`
Effective acceleration `g' = (a^2 + g^2)^(1/2)`
Time period `T = 2pisqrt(l/g) = 2 pisqrt(l/(g^2+a^2)^(1/2))`

(iv) If the bob of a simple pendulum is acted upon by additional forces of electrical, magnetic, buoyant, gravitational origin, the time period will increase or decrease according as the net acceleration in the downward direction is decreased or increased.

It is pendulum with period of oscillation 2 sec or period of swing 1 sec. Length of a second's pendulum at mean sea level, may be
calculated as follows.

From `T = 2 pi sqrt(l/g)` we have `l = (T^2 xx g)/(4 pi^2)`
Putting `T = 2` and taking `pi^2 > > g`
`l > > 1 m`

`text(Note :)`

A second's pendulum always bears a time period of 2 sec. however, the length changes with a change in acceleration due to gravity.

Pendulum Clocks gain time, if the time period of the pendulum decreases (due to decrease in length in winter or due to increase in ace. due to gravity, as when taken from equator to poles). For example, let the time period of a second's pendulum (originally) decrease to 1.99 sec. Now, each time, it oscillates, it counts 2 rather than 1.99 s. Thus, after a considerable no. of oscillations, the time counted or
shown by the clock is more than the actual time, and consequently, is goes fast.

Similarly, pendulum clocks loose time and go slow, when their time period increases.

Let `T` be the time period of clock pendulum of effective length `l`, showing the correct time.
Then `T = 2 pisqrt(l/g) ........ (1)`
Now, let `Deltatheta` be the change in temperature of the surrounding, the new length will be
`l^' = l (1 + alpha Delta theta )` [where `alpha` is the coefficient of linear expansion of the material of the pendulum]
The changed time period
`T^' =2 pi sqrt(l/g)`
`= 2pi sqrt({l(1+alpha Delta theta)}/g).................(2)`
Dividing equation (2) by (1)

`(T^')/T = sqrt(1+ alpha Delta theta) =(1+ alpha Delta theta)^(1/2) `


`=>(1+ 1/2 alpha Delta theta)` [Expanding by binomial expansion)

`T^' =T(1+ 1/2 alpha Delta theta)`

`Also((T^' - T)/T) = 1/2 alpha Delta theta`

i.e., Relative change in time period `= 1/2 alphaDeltatheta`
or, time lost or gained each second is `= 1/2 alpha Deltatheta`

`text(Note :)`

Unless otherwise stated, adopt the time period of clock pendulum as 2 sec.