(i) `P =` There exist a number which is equal to its square .
`~ P =` There does not exist a number which is not equal to its square.
(ii) `P =` For every real number `x, x` is less than `x + 1`.
`~ P =` There exist a number for which `x` is not less than `x + 1`.

There are three types of implications:
(i) "If ..... then"
(ii)"Only if"
(iii) "lf and only if"

( 1) "If ..... then" type of compound statement is called conditional statement.

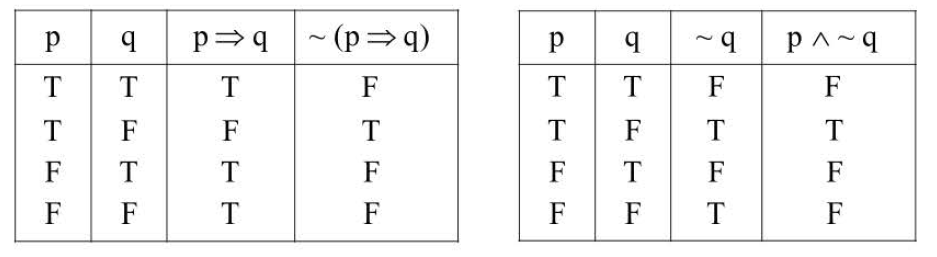
The statement `'if p` then `q' ` is denoted by `p-> q` (to be read as `'p` implies `q'`) or by `p => q`. Note that
`p -> q` also means
(i) `p` is sufficient for `q` (ii) `q` is necessary for `p` (iii) `p` only if `q`
(iv) `p` lead to `q` (v) `q` if `p` (vi) `q` when `p`
(vii) if `p`, then `q`


e.g. `p : a` number is a multiple of `9`
`q : a` number is a multiple of `3`.
Then `p -> q` or `p => q`


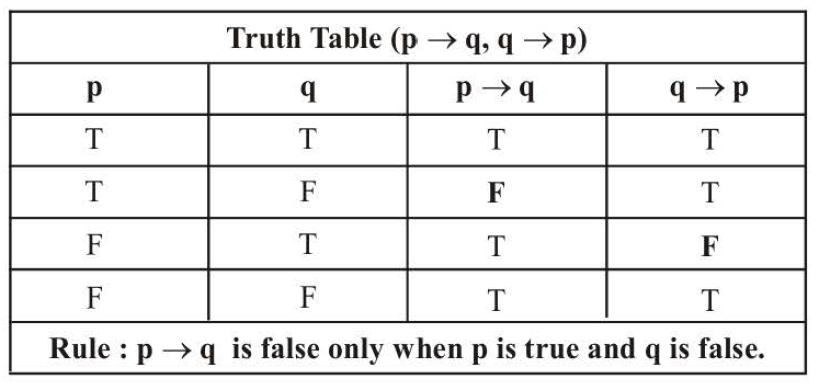
`p-> q` is false only when `p` is true and `q` is false. Truth table for `p-> q` is as follows.

"If and only if" type of compound statement is called Biconditional or equivalence or 'double
implication'. Symbolically 'p iff q' is represented by `p <-> q` or by `p <=> q`.
(i) `p` is a necessary and sufficient condition for `q`.
(ii) `q` is necessary and sufficient condition for `p`.
(iii) lf `p` then `q` and if `q` then `p`
(iv) `q` if and only if `p`.
e.g. `p:` If the sum of digits of a number is divisible by `3`, then the number is divisible by `3`.
`q :` if a number is divisible by `3`, then the sum of its digits is divisible by `3`.


A number is divisible by `3` if and only if the sum of its digits is divisible by `3`.
The following are other illustrations which actually do not appear to be so but they in fact are
biconditional.
(i) If you work hard only then you can succeed.
(ii) You can go on leave only if your boss permits. The truth table for biconditional is as follows:

Contrapositive and converse are certain other statements which can be fanned from a given statement
with "if .......... then".
Contrapositive of `p -> q` is `~ q -> ~ p`
e.g. If a number is multiple of `6` then it is multiple of `2`.
Contrapositive If a number is not multiple of `2` then it is not multiple of `6`.
Converse of `p -> q` is `q -> p`
e.g. If the angles of a triangle are equal then it is equilateral triangle.
Converse is if triangle is equilateral then angles of triangle are equal.


Note: Truth table for `p -> q` is same as its contrapositive.

If `p` and `q` are two statements, then

`~ (p => q) = p ∧ ~ q` `[ :. p => q -equiv ~p ∧ q ]`

Proof :

Negation of Biconditional statement or equivalence theorem:
lf `p` and `q` are two statement, then
`~ ( p <=> q) = ( p ∧ ~q) ∨ ( q ∧ ~ p)`


Proof :
`p <=> q = (p => q) ∧ (q => p)`
`:. ~ (p <=> q) = { (p => q) ∧ (q=> p)}`

`= [ ~ (p => q)] ∨ [ ~ (q => p)]`

`= (p ~q) ∨ (q ~p)`