Mathematics Process Of a Proof By Induction

Tautologies And Fallacies :

The compound statements (or propositions) which are true for any truth value oftheir components are
called 'Tautologies '.
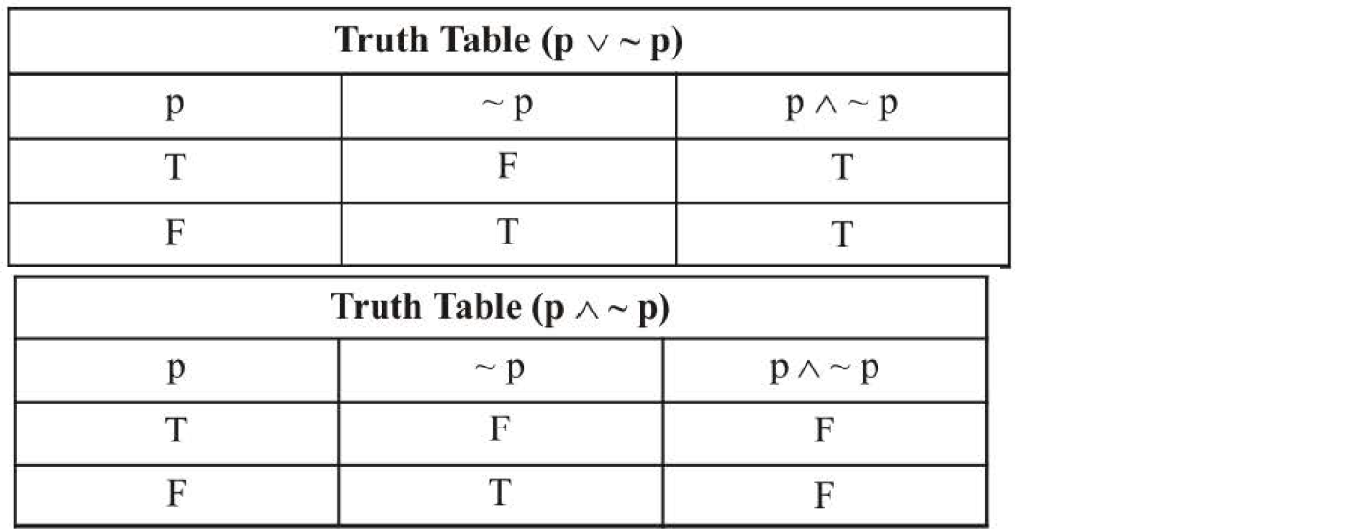
e.g. 'p ∨ ~ p' is a tautology, p being logical statement. This is illustrated by the truth table given below
which shows only Ts in the last column.

The negation of tautology is called a fallacy or a contradiction i.e. a proposition which is false for any
truth value of their components is called a fallacy. For example ` 'p ∧ ~ p '` is a fallacy, `p` being any logical
statement. This is illustrated by the truth table given below which shows only Fs in the last column.

Note :
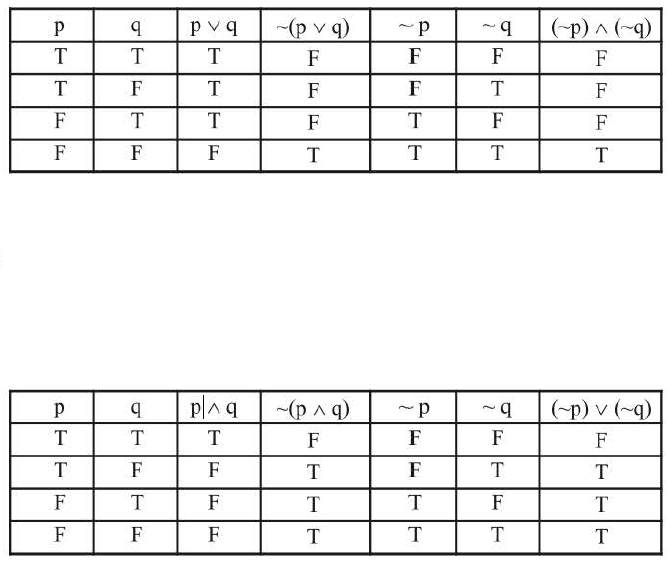
(i) `p ∨ q` is true iff at least one of `p` and `q` is true.
(ii) `p ⊻ q` is true iff exactly one of `p` and `q` is true and the other is false.
(iii) `p ∧ q` is true iff both `p` and `q` are true.
(iv) A tautology is always true.
(v) A fallacy is always false.

Algebra Of Statements :

Statements satisfy many Jaws some of which are given below-

(1) Idempotent Laws: lf `p` is any statement then
(i) `p ∨ p = p` (ii) `p ∧ p = p`

(2) Associative Laws: lf `p, q, r` are any three statements, then
(i) `p ∨ (q ∨ r) = (p ∨ q) ∨ r` (ii) `p ∧ (q ∧ r) = (p ∧ q) ∧ r`

(3) Commutative Laws : If `p, q` are any two statements, then
(i) `p ∨ q = q ∨ p` (ii) `p ∧ q = q ∧ p`

(4) Distributive Laws: lf `p, q, r` are any three statements, then
(i) `p ∧ (q ∨ r) = (p ∧ q) v (p ∧ r)` (ii) `p ∨ (q ∧ r) = (p ∨ q) ∧ (p ∨ r)`

(5) Identity Laws: lf `p` is any statement, `t` is tautology and `c` is a contradiction, then
(i) `p ∨ t = t` (ii) `p ∧ t = p` (iii) `p∨c = p` (i v) `p ∧ c = c`

(6) Complement Laws : If `t` is a tautology, `c` is a contradiction and `p` is any statement, then
(i) `p ∨ (~p) =t` (ii) `p ∧ (~p) =c` (iii) `~ t =c` (iv) `~c=t`

(7) Involution Law : lf `p` is any statement, then `~ (~p) = p`.

(8) De-morgan's Law: lf `p`and `q` are two statements, then

(i) `~ (p ∨ q) -equiv (~ p) ∧ (~q)` (ii) `~ (p ∧ q) -equiv (~ p) ∨ (~ q)`

(i) Proof :

`~( p ∨ q) -equiv (~p) ∧ (~q)`

(ii) Proof:

`~ ( p ∧ q) -equiv (~p) ∨ (~q)`

Inverse Relation :

If relation `R` is defined from `A` to `B` then the inverse relation would be defined from `B` to `A`, i.e

`R : A-> B => a R b` where `a in A, b in B`
`R^-1 : B ->A => b R a` where `a in A, b in B`

Here Doman of `R =` Range of `R^-1`
and Range of `R =` Domain of `R^-1`
` :. R^-1 = {(b, a) | (a, b) in R}`
`A` relation `R` is defined on the set of `1^(st)` ten natural numbers.

e.g. `N` is a set of first `10` natural nos ` :. N = {1 , 2, 3, ... , 10}` & `a, b in N`

`a R b => a + 2 b = 10`

`R = {(2, 4), (4, 3), (6, 2), (8, 1)}`
`R^-1 = {(4, 2), (3, 4), (2, 6), (1 , 8)}`

Identity Relation :

A relation defined on a set `A` is said to be an Identity relation if each & every element of `A` is related to
itself & only to itself

e.g. A relation defined on the set of natural nos. is
`aRb => a = b` where `a` & `b in N`
`R = {( 1 , 1), (2 , 2), (3 , 3), ......... }`
`R` is an Identity relation

Classification Of Relations :

(1) Reflexive: A relation defined on a set `A` is said to be an Identity relation if each & every element of `A` is
related to itself.
i.e. if `(a, b) in R` then `(a, a) in R`. However if there is a single ordered pair of `(a, b) in R` such `(a, a)
in R` then `R` is not reflexive.