DIFFERENT CASES OF BOUNDED AREA Different Cases of Bounded Area - BETWEEN TWO ORDINATES
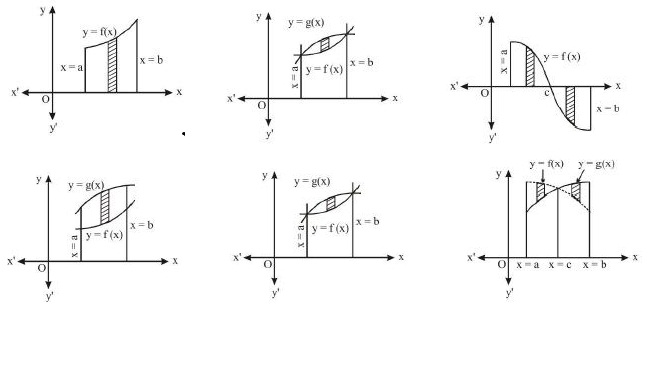
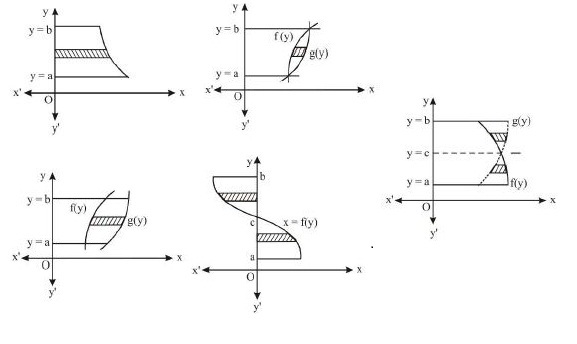
`1.` The area bounded by the continuous curve `y = f(x),` the axis of
`x` and the ordinates `x = a` and `x = b` (where `b > a`) is given by
`A = int_a^b f(x)dx = int_a^bydx`
`2.` The area bounded by the straight line `x = a, x = b (a < b)` and
the curves `y = f(x) andy = g(x)`, provided `f(x) < g(x)` (where
`a < x < b`), is given by
`A = int_a^b[g(x)-f(x)]dx`
`3.` When two curves `y = f(x)` and `y = g(x)` intersect, the bounded
area is
`A = int_a^b[g(x)-f(x)]dx ;` where `a < b`
where a and bare the roots of the equation `f(x) = g(x).`
`4.` If some part of a curve lies below the x-axis, then its area
becomes negative but area cannot be negative. Therefore, we
take its modulus.
If the curves crosses the x-axis at `c`, then the area bounded by
the curve `y = f(x)` and ordinates `x = a` and `x = b`
(where `b > a`) is given by `A = |int_a^cf(x)dx|+|int_c^bf(x)dx|`
`A = int_a^cf(x)dx - int_c^bf(x)dx`
`5.` The are abounded by `y = f(x)` and `y = g(x)` (where `a<= x <= b),`
when they intersect at `x = c in (a,b)` is given by
`A = int_a^b |f(x)-g(x)|dx`
or `int_a^b(f(x)-g(x))dx+int_c^b(g(x)-f(x))dx`
`x` and the ordinates `x = a` and `x = b` (where `b > a`) is given by
`A = int_a^b f(x)dx = int_a^bydx`
`2.` The area bounded by the straight line `x = a, x = b (a < b)` and
the curves `y = f(x) andy = g(x)`, provided `f(x) < g(x)` (where
`a < x < b`), is given by
`A = int_a^b[g(x)-f(x)]dx`
`3.` When two curves `y = f(x)` and `y = g(x)` intersect, the bounded
area is
`A = int_a^b[g(x)-f(x)]dx ;` where `a < b`
where a and bare the roots of the equation `f(x) = g(x).`
`4.` If some part of a curve lies below the x-axis, then its area
becomes negative but area cannot be negative. Therefore, we
take its modulus.
If the curves crosses the x-axis at `c`, then the area bounded by
the curve `y = f(x)` and ordinates `x = a` and `x = b`
(where `b > a`) is given by `A = |int_a^cf(x)dx|+|int_c^bf(x)dx|`
`A = int_a^cf(x)dx - int_c^bf(x)dx`
`5.` The are abounded by `y = f(x)` and `y = g(x)` (where `a<= x <= b),`
when they intersect at `x = c in (a,b)` is given by
`A = int_a^b |f(x)-g(x)|dx`
or `int_a^b(f(x)-g(x))dx+int_c^b(g(x)-f(x))dx`